人工神经网络在调制识别中的应用综述

张承畅，余 洒，徐 余，罗 元

(重庆邮电大学 光电工程学院，重庆 400065)

0 引 言

非合作通信[1-2]中接入到通信系统的未经授权的第三方，其对发送端的已调信号相关调制信息(如调制方式、相关参数)是未知的。而非合作通信的目的是在没有任何调制信号的先验信息的情况下，确定信号的调制类型和相关参数，从而进一步完成信号或干扰的识别、威胁评估等任务。信号的调制方式识别主要发生在非合作通信系统中。

在军事领域，电子信息战中敌方信号的干扰识别与反干扰，威胁探测、评估与告警，目标捕获与搜索等任务都离不开调制识别技术[3]。而在民用领域，无线电资源管理部门需要应用调制识别技术对无线电频谱资源进行监测与管理[4-5]，对非法用户进行监听与定位，防止未经授权用户使用公共频谱资源，从而保障合法用户的正常通信。

在接收端，信号的调制方式识别是信号检测和信号解调之间的关键一步，三者之间的关系如图1所示。

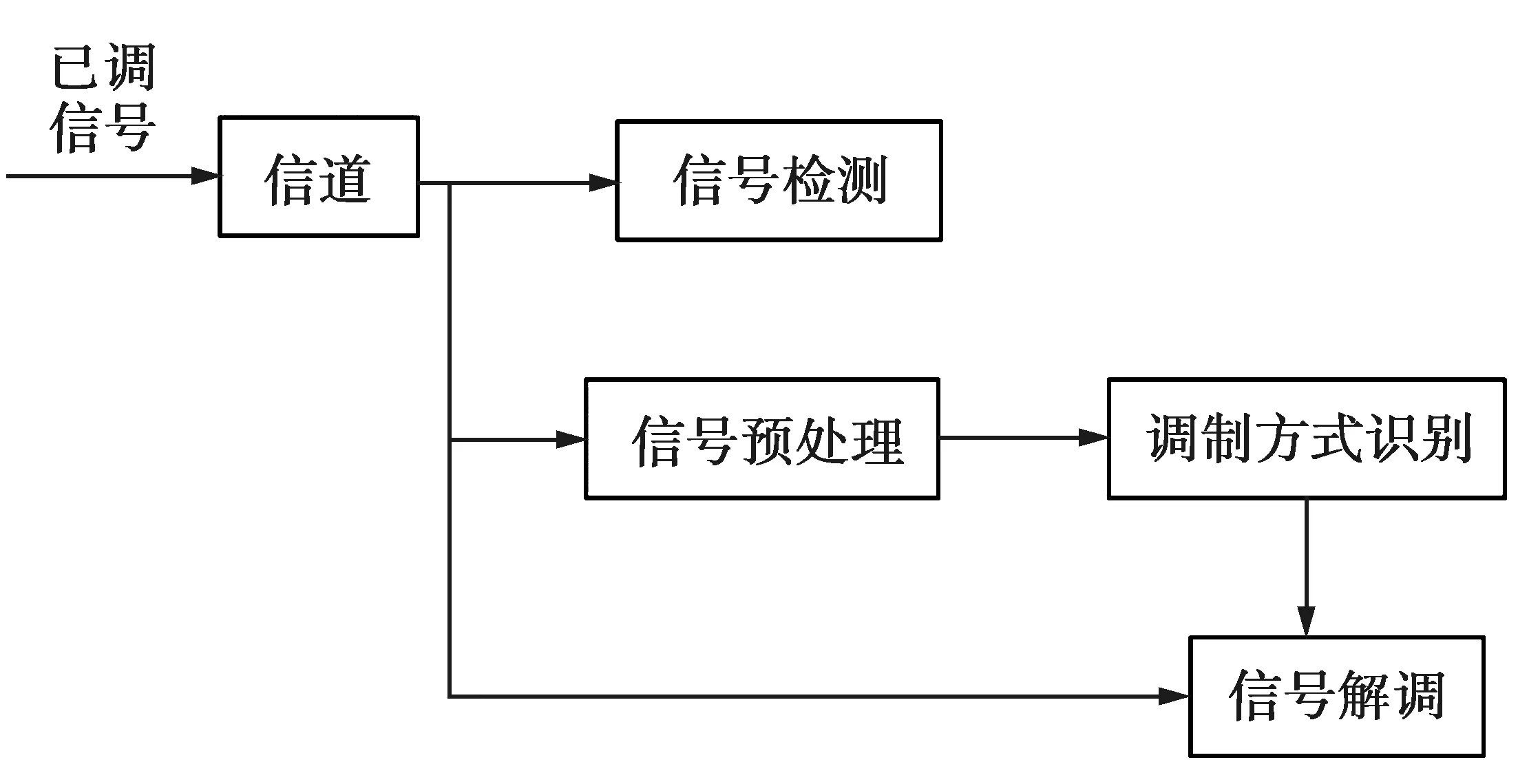
图1 信号检测、调制方式识别以及信号解调间的关系Fig.1 Relationship between signal detection, modulation moderecognition and signal demodulation

按照信道中传输信号的不同，可以将通信系统分为数字通信和模拟通信。相较于模拟通信，数字通信抗干扰能力更好、抗信道损耗能力更强、安全性更高，且传输差错可控，已广泛应用于各个领域。数字信号调制方式[6]按照调制到的载波参数的不同可以分为幅度键控(amplitude shift keying, ASK)、频移键控(frequency shift keying, FSK)、相移键控(phase shift keying, PSK)；除此之外，还有正交幅度调制(quadrature amplitude modulation, QAM)、正交频分复用调制(orthogonal frequency division multiplexing, OFDM)、高斯最小频移键控(gaussian minimum-shift keying, GMSK)等调制方式。在非合作数字通信系统中，如何对繁多的数字信号调制方式进行正确识别是一项具有挑战性的工作。

1 调制方式识别技术

1.1 调制识别技术简介

信号的调制方式识别[7]可以分为信号预处理、特征提取、分类识别3个部分。具体流程如图2所示。

图2 调制方式识别流程Fig.2 Modulation mode recognition process

图2中，信号预处理的目的是为之后的特征提取部分提供易处理和分析的数据。信号预处理过程主要包括数字下变频、信号滤波等步骤。特征提取主要是针对待识别信号类型的不同，提取出可以区分不同调制方式的信号。

早期的信号调制识别是通过对测量参数的人工解译来实现的，严重依赖操作人员的技术水平和工作经验。人工识别方法主观性很大、效率很低、实时性很差，在面对复杂调制方式尤其是数字调制方式时其结果不能尽如人意。1969年4月，在斯坦福大学技术报告上第一篇研究调制方式自动识别的论文[8]得以发表，由此开启了信号自动调制识别的大门。

1.2 调制识别技术的发展历程

随着通信技术由模拟向数字的转变，调制方式愈加复杂，各种针对调制方式识别的算法研究也迅速展开。文献[9]利用幅度和频率变量提出一种基于决策理论和模式识别的方法对ASK、FSK和PSK信号进行分类识别；文献[10]提出一种近似似然率分类器来对BPSK、QPSK信号进行分类；文献[11]提出可以利用信号的循环自相关函数和循环功率谱密度函数来进行调制识别；文献[12]提出应用小波变换来进行数字通信信号识别的方法。以上方法都基于传统的假设检验或者特征提取方法来进行信号调制方式识别，具有完整的理论支撑，但是计算复杂度高，识别效果一般，尤其在面对复杂电磁环境、低信噪比等情况时，识别效果并不尽如人意。

随着人工智能、机器学习等技术的出现，人工神经网络(artificial neural networks, ANN)作为分类器应用于调制识别逐渐成为研究热点。ANN应用于调制识别最早可以追溯到1996年，文献[13]提取信号的瞬时值为特征向量，利用人工神经网络作为分类器完成多种模拟数字信号的调制识别。文献[14]提出一种基于小波变化理论和多层神经网络的方法，对MASK、MFSK以及MPSK信号进行调制识别；文献[15]提出一种基于循环谱的BP神经网络，对MQAM信号进行识别；文献[16]提出一种基于信号的二阶及四阶统计量的两层感知器神经网络，对 FSK、PSK、ASK、QAM进行识别，识别率高达 0.7～0.99。基于ANN的调制识别方法能够适应电磁环境的变化，在低信噪比下的调制识别效果也很好，因此，得到了越来越广泛的研究和应用。

1.3 调制识别技术的分类及原理

经典的调制识别方法可以分为两大类：基于假设检验的最大似然(likelihood based, LB)方法和基于特征提取(featured based, FB)的模式识别方法。详细的分类如图3所示。

图3 信号调制识别方法分类Fig.3 Classification of signal modulation recognition methods

1.3.1 基于假设检验的最大似然方法

基于假设检验的最大似然方法[17-18]可以看作是多重假设检验问题。它是在有背景干扰的条件下对所截获信号的检验统计量(通常采用似然比函数)进行理论推导，寻找合适的门限，然后在贝叶斯代价最小准则下进行判决。使用基于假设检验的最大似然方法流程如图4所示。

0≤t≤NT,i=1,2,…,Nmod

(1)

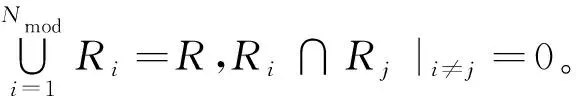
图4 基于假设检验的最大似然估计方法流程Fig.4 Process of the maximum likelihood estimate based on hypothesis testing

按照计算似然函数时对未知参数处理方式的不同，基于假设检验的最大似然方法可以分为：①平均似然比[19]检测(average likelihood ratio test, ALRT)。将未知参数看成概率密度函数已知或者可以假设为某种概率密度函数的随机变量，求出似然函数针对该参数的均值。②广义似然比检测[20](generalized likelihood ratio test, GLRT)。将未知参数看成确定性变量，用极大似然估计方法求出参数在不同假设下的估计值。③混合似然比检测(hybrid likelihood ratio test, HLRT)。是ALRT和GLRT的结合方法，它将一部分未知参数当作随机变量，按照ALRT的方法对其PDF求平均；另一部分未知参数当作其值未知的确定变量，按照GLRT的方法求其最大似然估计值。基于假设检验的最大似然法适用于已知较多先验信息且对识别种类数量没有特殊要求的离线处理。该方法具有完备的理论基础，能够得到识别性能理论曲线，并保证在贝叶斯最小误判代价准则下其分类效果最优。但似然函数推导复杂，未知变量较多时计算量大，难以处理；加之似然函数的参数均是由特定条件下的信号推导得到的，因而只适用于特定环境的调制识别问题。

1.3.2 基于特征提取的模式识别方法

基于特征提取的模式识别方法[21-22]运用特征提取实现调制方式识别，需要选择合适的分类器来进行分类识别。分类器的任务是：根据某一准则把一个给定的由特征向量表示的输入模式归入到一个适当的模式类别，完成从特征空间到判决空间的映射，最终给出识别结果。

在基于特征提取的调制识别方法中，常用的特征有时域特征，频域特征和变换域特征3种。

1)信号的时域特征

信号的时域特征主要包括瞬时频率、瞬时相位及瞬时幅度。根据信号的这3个瞬时参量，可以计算其瞬时统计量作为特征。常见的瞬时统计量有：零中心归一化瞬时幅度绝对值的标准差、零中心非弱信号段瞬时相位非线性分量绝对值的标准偏差、零中心非弱信号段归一化瞬时频率绝对值的标准偏差等。这些瞬时参量的计算方法归纳如下。

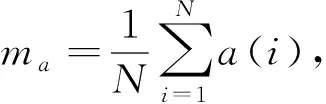
(2)

不同的瞬时特征可以区分出对应参数(幅度、相位、频率)不同的调制信号。基于瞬时值统计特征的调制识别算法，无需对信号有任何先验知识，预处理要求低，算法复杂度相对较低。但在面对衰落信道时，由于分类器学习能力限制，对识别结果影响较大，因此，在低信噪比以及衰落环境下，分类器的学习能力有待进一步提升。

2)信号的频域特征

信号的频域特征主要有：高阶累积量、循环谱等。信号的高阶累积量可以表征信号的高阶统计特征，由于高斯白噪声的某些高阶累积量恒等于零，并且调制信号的高阶统计量有很好的抗衰落特性，因此使用信号的高阶累积量进行调制识别的效果较好。信号x(t)的高阶累积量如下所示。

C20=cum(X,X)=M20

C21=cum(X,X*)=M21

C41=cum(X,X,X,X*)=M41-3M21M20

(3)

(3)式中，M为信号的混合矩。

Mpq=E{[x(t)]p-q[x*(t)]q}

(4)

通信信号通常具有循环平稳特性，信号的循环谱在循环频率不为零处有较大的非零值，而平稳噪声或近似平稳噪声的循环谱主要集中在零循环频率处，因此循环谱能够很好地抑制平稳噪声和干扰，利用非零循环频率处的循环谱特征能很好地识别出信号的调制方式。信号的循环谱(即循环自相关函数的傅里叶变换)表达式如下。

(5)

(6)

(6) 式中，T为信号持续时间。

3)信号的变换域特征

信号的变换域特征主要有：小波变换、短时傅里叶变换(short-time fourier transform, STFT)、星座图等。其中小波变换是一种介于函数的空间域(时间域)表示和频率域表示之间的局部变换方法。它通过伸缩、平移等运算方式对信号进行多尺度的细化分析，从而能够有效地从信号中提取所需要的信息。对于待识别信号x(t)，其连续小波变换(continuous wavelet transform, CWT)的表达式为

(7)

(7)式中：a为尺度因子；τ为平移因子；*表示复共轭运算；Ψ(t)为小波函数。

短时傅里叶变换(STFT)在傅里叶变换的基础上通过窗函数截取一段平稳信号，再对得到的信号做傅里叶变换，信号x(t)的STFT表达式如下。

(8)

(8)式中：τ为窗函数长度；g(t)为窗函数。τ越大，截取的信号越长，傅里叶变换后频率分辨率就越高，而时间分辨率就越差。因此，在确定窗函数长度时要谨慎选取。

1.3.3 分类器

常用的分类器有：决策树[23]分类器、最近邻(k-nearest neighbor, KNN)[24]分类器、贝叶斯分类器[25]、支持向量机(support vector machine, SVM)[26]、随机森林[27]以及人工神经网络(ANN)[28-33]分类器等。

决策树分类器是一种逼近离散值目标函数的二分类方法。它将分类规则以树状结构表示，采用多级分类结构，每级结构根据一个或多个特征参数，分辨出某种调制类型，最终能完成多种信号调制类型的识别。该算法结构简单，但是需要预先确定判决门限，自适应性差。

KNN分类器是一个基于距离的分类算法。其基本原理是：对于一个新的样本，找出距离它最近的K个训练样本，然后采取“少数服从多数”的决策方法，得到该样本所属的类别。该算法计算简单，识别效率较高。

贝叶斯分类算法是描述一组变量的概率分布的有向图，它通过条件概率来指定条件独立性假设，可以将复杂问题分解为若干简单模型以便于有效地处理，学习得到的模型也很容易满足模型解释要求。该算法理论基础完备，但计算复杂度高，实现复杂。

支持向量机(SVM)是一种建立在统计学习理论和结构风险最小化原理基础上的机器学习方法，为解决有限样本学习问题提供了一个统一的方案。SVM通过事先选择的非线性映射(核函数)将输入向量映射到一个高维特征空间，在高维空间对非线性问题进行分类。

随机森林是一种统计学习理论，利用bootsrap抽样方法从原始样本中抽取多个样本，对每个bootsrap样本进行决策树建模，然后组合多棵决策树的预测，通过投票得出最终预测结果。随机森林具有很高的预测准确率，对异常值和噪声具有很好的容忍度，且不容易出现过拟合现象。

总体来看，以上分类器计算复杂度较高，实现具有一定的困难，而且对于恶劣通信环境识别的性能较差。

人工神经网络分类器是一种模仿生物神经连接产生特征向量与分类类别之间映射的非线性变换技术，通过调整内部节点之间相互连接的关系达到处理信息的目的。常用于分类器的ANN主要有BP神经网络、卷积神经网络等。ANN分类器虽然理论支撑不够完备，但是实现简单，在信噪比较低的情况下也有较好的识别效果。

2 人工神经网络(ANN)

2.1 多层感知器神经网络

单层感知器即神经元模型是神经网络中最基本的模型，其结构如图5所示。

图5 单层感知器模型Fig.5 Single layer perceptron model

图5中，xi(i=1,2,…,r)表示输入到感知器中的信息，每个输入对应一个权值wi，感知器的输入与权值进行相乘求和，再经过激活函数之后得到输出。激活函数表示的是上层节点输出与下层节点输入间的关系，一般采用非线性函数，由此可以提高网络的逼近和泛化能力。

设激活函数用f(·)表示，则输出y可以表示为

(9)

常用激活函数有：Sigmoid函数、Tanh函数、ReLU函数等，其表达式分别为

(10)

(11)

(12)

单层感知器并不能解决复杂的非线性问题，由此出现了多层级联的感知器，即多层感知器(multi-layer perceptron, MLP)神经网络[34]。MLP神经网络[35]又称为多层前馈神经网络，网络中相邻两层神经元之间相互级联，同一层节点之间没有相互连接，第一层为输入层，最后一层为输出层，中间可以包含一个或多个隐藏层，从而构成全连接神经网络。MLP网络是最基础的神经网络，其激活函数通常选用Sigmoid函数。

2.2 反向传播(back propagation, BP)神经网络

由于MLP神经网络并不能很好地完成网络性能的训练，因此出现了BP神经网络[36-38]。对误差使用反向传播(BP)算法的多层感知器神经网络就称为BP神经网络，它是目前应用最广泛的神经网络之一，包括输入层、隐藏层和输出层，其中隐藏层可以有多个。只有一个隐藏层的BP神经网络如图6所示。

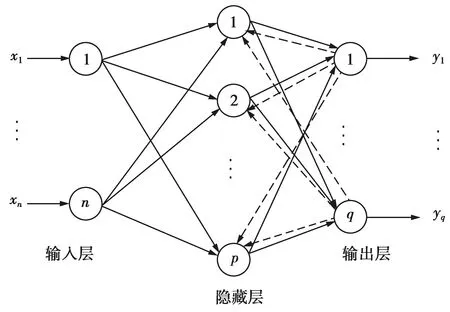
图6 单隐层BP神经网络Fig.6 BP-Network with one hidden-layer

图6中，实线代表前向传播，主要是指输入信息经过处理之后向输出方向传输。在隐藏层中，输入与权值相乘，再经过激活函数之后输出。虚线代表反向传播，是指输出层节点的实际输出与期望输出之间的误差从输出层向输入层方向传输，直到误差传输至紧邻输入层的隐藏层。误差反向传播的目的是进行权值调整使得误差减小，即实际输出越来越接近期望输出。BP神经网络常用的激活函数为Sigmoid函数。

BP神经网络具有很强的非线性映射能力，而且可以根据具体的问题设置隐藏层个数以及每一层的神经元数量，比较灵活；但是其学习速度慢且容易陷入局部极小值。

2.3 卷积神经网络(convolutional neural network,CNN)

卷积神经网络[39-41]是一种深度神经网络，每一层都包含多个由神经元组成的二维平面，在图像处理方面有着独特的优势。CNN主要由卷积层、池化层和全连接层组成。其中，卷积层的主要作用是提取图像的特征，池化层的主要作用是下采样，而全连接层的主要作用是分类。

卷积层是卷积神经网络的核心，每一个卷积层中的卷积核共享权值(即每一个卷积层中的卷积核是相同的)，从而降低了计算复杂度；而池化层的池化操作通常有两种：平均池化(即选取指定区域的平均值代表整个指定区域)和最大池化(即选取指定区域的最大值代表整个指定区域)；全连接层负责将提取的特征进行非线性组合得到输出，这一层需要将池化层的输出与权重相乘再加上偏置，之后使用非线性激活函数得到输出，网络参数的优化通常使用梯度下降法或反向传播算法。CNN常用的激活函数是ReLU函数。

由于卷积神经网络主要用于图像识别领域，因此在将CNN用于调制方式识别时通常与信号的星座图特征一起使用，但是信号的星座图重构受参数估计的精度影响比较大，因此，信号的重构星座图在低信噪比情况下往往质量较差，不利于调制方式的正确识别。

2.4 ANN在调制识别中的应用

将ANN作为分类器应用于调制识别的流程如图7所示。

图7 基于ANN的调制识别流程Fig.7 Process of modulation recognition based on ANN

图7中，关键的步骤在于特征参数提取以及ANN分类器训练优化。其中特征参数需要针对待识别信号的不同而确定，如1.3小节所述。

对ANN分类器进行训练时， BP神经网络会出现陷入局部最小值、收敛速度慢的问题。因此，需要对网络的参数进行优化，这是将神经网络应用于调制识别的难点所在。实现网络参数优化的方法流程如图8所示。

图8 使用算法优化ANN分类器流程Fig.8 Process of optimizing the ANN classifier using algorithms

用于神经网络参数优化的算法主要有：遗传算法(genetic algorithm, GA)、粒子群算法[32](particle swarm optimization, PSO)等。

遗传算法(GA)是一种模拟自然界遗传机制和生物进化论的并行随机搜索最优化方法。该算法将自然界“优胜劣汰，适者生存”的生物进化原理引入优化参数形成的编码串联群体中，按照所选择的适应度函数并通过遗传中的选择、交叉和变异操作对个体进行筛选，使适应度值好的个体被保留，适应度值差的个体被淘汰，新的群体既继承了上一代的信息，又优于上一代。这样反复循环，直至满足条件。

粒子群算法(PSO)算法也属于进化算法的一种，它从随机解出发，通过迭代寻找最优解，通过适应度值来评价解的好坏，但它没有遗传算法的“交叉”和“变异”操作，只是通过追随当前搜索到的最优值来寻找全局最优。该算法实现容易、精度高、收敛快。

3 调制识别研究现状

基于假设检验的最大似然估计方法和使用支持向量机、贝叶斯、随机森林这些分类器的基于特征提取的调制识别方法都属于传统的调制识别技术。近年来，随着人工智能的不断发展，人工神经网络作为分类器逐渐应用于调制识别中。

3.1 传统调制识别技术的发展

文献[42]针对MPSK信号的调制识别问题，对最大似然估计法进行改进，提出一种压缩域最大似然估计的调制识别新方法，降低了计算复杂度，提高了低信噪比下算法的识别性能。文献[43]针对航空信道下MQAM信号的类内识别，提出了基于假设检验的平均似然比识别算法，能够显著地改善信号的识别性能，同时还能够很好地抵抗信道衰落和多普勒频移。文献[44]针对LPI雷达信号的识别，提出了一种基于栈式自编码和支持向量机的方法，该算法在低信噪比、小样本情形下能够对雷达信号进行有效识别。文献[45]提出一种用粒子群优化算法来优化支持向量机参数的方法，该方法在参数优化方面具有良好的鲁棒性、快速收敛和全局搜索能力，具有更高的分类精确度和效率。文献[46]针对未知噪声和时变信道的挑战，提出了一种新的基于粒子滤波和贝叶斯推理的自适应调制识别算法，在信噪比为12 dB时识别率可达到99.8%。文献[47]借助随机森林算法和信号的时域特征参数，对6种典型的低阶数字调制信号进行自动分类识别，在信噪比不小于3 dB的条件下，所提算法的调制识别正确率接近100%。

传统的调制识别算法具有比较完备的理论体系，但是往往数学推导复杂，计算复杂度大，且在复杂多变的信道环境下适用性较差。

3.2 基于神经网络的调制识别技术的发展

文献[48]通过变梯度BP修正算法对神经网络进行训练，以提高收敛速度，缩短训练时间。在信噪比为10 dB时，识别率达到95%。文献[49]设计了一种CNN-LSTM并联网络，直接将同向分量和正交分量作为输入数据，上下支路提取信号的空间和时间特征，该算法无需人为设计特征参数，在低信噪比下具有较好的识别性能。文献[50]提出一种改进的卷积神经网络结构，可实现对7种不同的调制信号的分类。在信噪比不小于5 dB时，识别率可达97.99%；当信噪比不小于9 dB时，识别率可达100%。文献[51]针对基于有监督学习通信信号分类算法需要大量有标签训练样本，而在实际场合大多无法满足数量要求的问题，提出利用数据驱动模型的半监督学习方法。较以往方法，其识别准确率提升3%～20%；小样本条件下性能提高60%；同时，在低信噪比条件下识别能力突出，0 dB时对11种调制信号平均识别正确率达到92%，具有明显优势。

文献[52]针对当前调制识别模型缺乏泛化性的缺点，提出了一种基于卷积神经网络的鲁棒自动调制识别方法，能够对15种信号进行识别，而且在低信噪比下识别准确性也很好。文献[53]针对STBC信号的调制识别问题，提出了一种基于卷积神经网络的方法，该算法无需信号的先验信息，在较低的信噪比下识别效果较好。文献[54]针对当前通信信号的制式识别算法在低信噪比情况下识别不准确的问题，提出一种新的小波特征与改进的深度神经网络结合(WL-DNN)的识别算法，该算法在信噪比低至0 dB的情况下，单个调制信号最低识别率超过95%，平均识别率超过98%。文献[55]针对弹性光网络中的信号调制识别问题提出了一种基于神经网络和查找表的方法，该方法在通信误码率大于102的OSNR范围内，可以正确识别接收信号的调制格式。文献[56]提出了一种新的深度几何卷积网络(deep geometric convolutional network, DGCN)，用于从信号的Wigner-Ville分布图中分层提取鉴别特征，该网络能够对15种调制信号进行高精度分类。

3.3 当前存在的问题及发展方向

通过对目前神经网络在调制识别中的应用调研可以看出，目前ANN在调制识别上的应用可以分为两大类。一类是基于卷积神经网络的调制识别算法，该类方法将信号的调制识别问题转换为图像识别问题，不需要任何信号的先验信息，重难点在于信号的图形特征提取；另一类是基于深度神经网络(如BP神经网络)的调制识别算法，该类方法将ANN作为分类器进行识别，重难点在于网络训练时参数的优化。总的来说，基于人工神经网络的调制识别方法识别准确率高、对信号的预处理不复杂。

调制识别技术已历经半个多世纪的发展，传统的识别理论已相当成熟。但是随着通信系统的不断发展，调制识别技术仍需不断改进才能满足需求。而随着人工智能技术的不断发展，将人工神经网络模型应用于调制识别已成为主流的发展方向。但是人工神经网络在调制识别中的应用目前存在的主要问题有：一是现有的算法基本上都是针对一类或两类信号的识别而搭建的模型，并不能够对多类信号进行准确识别，即算法的普适性不够高；二是现有算法基本上都需要经过大量样本的训练才能够对信号进行准确识别，从而忽略了小样本情况下信号识别准确度的问题。

因此，笔者认为基于神经网络的调制识别算法主要有两大发展趋势：一是对ANN模型进行深入研究，构建能够对多种信号进行识别的网络模型，使得算法更具有普适性；二是从网络参数入手，利用相关算法对网络模型参数进行优化，提高准确度的同时尽可能降低样本数量及训练时间。

3.1小节和3.2小节分别论述了近年来国内外关于调制识别的经典方法和基于神经网络的调制识别方法。表1为这两类方法的总结对比分析。

表1 调制识别方法总结

4 总结

无线通信技术的不断发展对非合作通信中调制方式的识别提出了更高的要求，而当前人工智能的不断发展为调制识别技术的发展提供了新的契机。本文着重介绍了人工神经网络模型在调制识别中的应用。通过对当前研究的分析发现，如今调制识别主要存在的问题是低信噪比下识别精度低；而人工神经网络在调制识别中的模型没有针对性和普适性。因此，未来对调制识别的研究主要集中在人工神经网络模型的构建以及低信噪比下识别精度的提高这两个方面。