航空甚高频频率使用与航班总量关联及预测分析

赵国栋，刘播阳，程思备，蒋博筹，骆 骁，邓丽莉

(1.重庆市无线电监测站，重庆 400020； 2.重庆信息通信研究院，重庆 401336)

0 引 言

无线电频谱资源是一种稀缺的战略性资源，其可用范围和应用领域不断被扩展，在国民经济发展中也不断做出新的贡献，如何科学评估频谱资源的使用情况并建立其与区域经济发展的关系已引起广泛关注。

在频率使用率测试指标方面，国际电信联盟在《频谱占用度测量建议书》(ITU-R SM.1880)和《频谱监测手册》(2011版)中对于频率使用率的相关评价参数如频段占用度等做出了规定。《无线电频率使用率要求及核查管理暂行规定》(工信部无[2017]322号)规定，采用频段占用度、年时间占用度、区域覆盖率和用户承载率4个指标对频率使用率进行评价。国内各省级无线电管理机构在2018年开展了频率使用率专项测试和评估，但对测试数据的挖掘和应用仍需深入。在认知无线电(cognitive radio,CR)领域，根据不同的用途，频谱占用模型大致分为两大类[1]:①信道占用/空闲分析，主要用于预测具体信道的占用状态、避险接入冲突，适用于频谱动态共享[2-3]，更为偏向微观层面分析，主要分析方法包括马尔可夫过程[4]、博弈模型[5]等；②频率使用行为分析，采用统计学或计量经济学相关理论，对长周期的频率使用统计数据进行建模分析，从而获取频率使用的用户行为特性或者周期特性，适用于宏观分析，典型方法有时间序列分析[6]、Beta分布[7-8]等。

本文依据国际电信联盟及国家无线电管理机构相关测试标准，采用重庆市无线电监测站固定监测站木耳站对重庆江北国际机场航空甚高频频段的信道占用度进行专项测试，确定数据满足向量自回归(vecter autoregression,VAR)建模的相关条件后，构建模型并分别对信道时间占用度、航班总量2个序列进行稳定性检验和相关分析，并对后续9天的航班流量进行预测。进一步对比仅采用航班数据的构递差分整合移动平均自回量模型(autoregressive integrated moving average model,ARIMA)模型预测的后续9天航班流量，发现联合信道占用度和航班数据的VAR模型预测精度更高，为深度挖掘频谱监测数据价值提供了新的启示。

1 数据获取及预处理

1.1 数据获取

航空甚高频通信系统是保证其在飞行过程中飞机与地面之间以及飞机与飞机之间能够保持相互联系的通信工具，其使用的频段为118～135.975 MHz，信道间隔为12.5 kHz，属于专用频段。本论文采用重庆市无线电监测站固定监测站木耳站对重庆江北国际机场航空甚高频频段的信道占用度进行专项测试，测试周期3个月(2020年4月2日—7月2日)，测试时段为9:30至次日9:30，木耳站控制界面如图1所示，监测频段为117.975～137 MHz，电平门限为12 dBμV，扫描速度为12.92 GHz/s。信道占用度与航班起降总量数据分别如表1，表2所示。

图1 系统控制界面图Fig.1 System control interface diagram

表1 2020年4—7月江北机场航空甚高频频段信道占用度与航班起降总量数据

表2 ADF检验结果

1.2 数据预处理结果

分别对信道时间占用度(Y)和航班序列(X)的本阶和一阶序列进行检验，发现两序列的本阶序列不平稳，但一阶序列平稳。

进一步对航班序列(X)的一阶序列进行相关分析，如图2所示。其中，自相关图像、偏相关图像均拖尾，满足典型的ARIMA模型的基本特征，与文献[9]中的总体趋势一致。

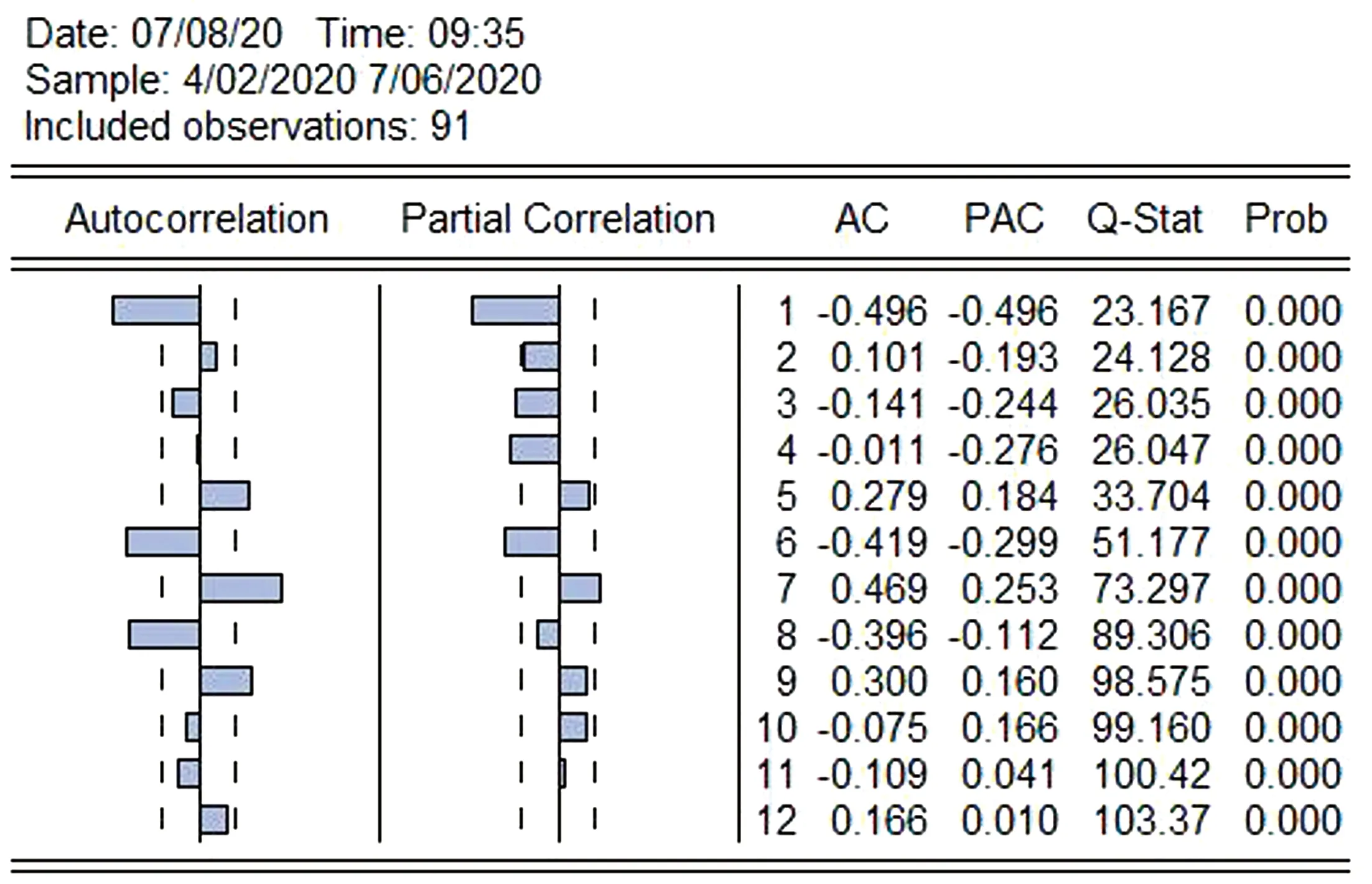
图2 航班总量序列的相关分析Fig.2 Correlation analysis of total flight sequence

2 VAR模型理论及建立

2.1 VAR基本理论

VAR模型是多个自回归模型的联立形式，所以称向量自回归模型，在其每个方程中，所有的解释变量对模型中其他解释变量的滞后项进行回归，以此估算出内生变量间的相互动态的关系，其表达式为[10]

yt=A1yt-1+…+Akyt-k+Bxt+σt

(1)

(1)式中：yt是内生变量的列向量；xt是外生变量的列向量为通常在做VAR模型分析时设置为常数，Bxt被称为截至距项；A1，…，Ak，B为待估计矩阵；k代表最优滞后期；σt为误差列向量。

本论文目的为研究信道时间占用度与航班进出港总量的关系，故内生列向量含有2个元素，其表达式为

(2)

(2)式中，Yt和Xt分别代表t期(本论文为天)航班进出总量以及信道时间占用度。

当VAR模型中的所有变量满足同阶单整条件并存在协整关系时，可以将VAR模型修正为向量误差修正(vector error corvedion,VEC)模型，VEC模型的实质是有协整约束的VAR模型。

VEC模型的表达式为

Δyt=αECMt-1+A1Δyt-1+…+AkΔyt-k+εt

(3)

(3)式中：ECM表示根据协整方程计算的误差修正项；k代表最优滞后期；εt为k维扰动列向量。

2.2 VAR模型建立基本步骤

在满足序列平稳的条件下，将信道时间占用度与航班总量构建VAR模型。总体步骤如下。

步骤1平稳性检验及协整检验。检验序列的平稳性，并判断序列是否满足同阶单整条件，若满足同阶单整条件则表明存在协整关系，需建立协整方程以便后续对VAR模型进行修正。

步骤2确定滞后期并构建VAR模型。依据似然比检验(LR)、最终预报误差准则(FPE)、赤池信息准则(AIC)、施瓦兹准则(SC)及汉南奎因准则(HQ)确定变量的滞后期。选定滞后期后，即可构建VAR模型并确定表达式。

步骤3格兰杰因果检验。判断信道时间占用度与航班总量之间是否存在格兰杰因果关系，即信道时间占用度是否有助于预测航班总量或者航班总量是否有助于预测信道时间占用度。

步骤4脉冲响应分析。分析一个变量受到其他变量冲击所带来的影响，本文主要研究航班总量对信道时间占用度的随机扰动冲击所做出的响应。

步骤5利用已通过检验的模型进行预测分析。预测方法常用有两种：静态预测与动态预测。将预测值与实际值作对比分析，得出相应结论。

3 关联及预测分析结果

3.1 协整检验

对信道时间占用度(Y)和航班序列(X)进行协整检验，检验结果如表3所示。

表3 协整检验分析

经检验表明，在没有趋势项和截距项的情况下，迹检验与最大特征值检验均存在协整关系，协整检验的结果如表4所示。

表4 协整检验结果

由于dY的调整系数为负(-0.211 313)，偏离非均衡误差可以得到修正，表明协整关系是有效的，dX的调整系数为正(5.19E-05)，表明偏离非均衡误差无法得到修正，若进行修正误差会更大，可认为协整关系无效。根据对数似然值最大的协整关系可知长期均衡方程为

Yt=-1 690.352Xt+εt

(4)

(4)式中：t表示天数；εt为误差修正项。

3.2 滞后期选择与VAR模型构建

依据LR，FPE，AIC，SC及HQ计算各滞后期的统计量如表5所示。

表5中给出了0～8阶模型的LR，FPE，AIC，SC，HQ值，并以“*”标记出依据相应准则选择出来的滞后阶数。滞后期为7时有3个最优统计量，故模型最适合的滞后阶为7，最佳模型为VAR(7)，表达式为

(5)

(5)式中：Y表示航班总量；X表示信道时间占用度；εt为扰动项。

表5 VAR模型各滞后期的统计量

由于两序列协整关系的存在，需修正VAR模型，即构建VEC模型。受协整条件约束，VEC模型的滞后期比VAR模型少1期，因此，构建滞后期为6的VEC模型，VEC模型中的协整关系用误差修正项表示为

CointEQt=Yt-1-1 690.352Xt-1+804.779 1

(6)

3.3 格兰杰因果检验

表6为格兰杰因果检验结果，经检验发现，在0.05的置信水平下，信道时间占用度增长不是航班总量增长的格兰杰原因的概率为0.048 6，表明信道时间占用度增长对航班总量增长构成格兰杰因果关系，即分析信道时间占用度有助于预测航班总量。

表6 格兰杰因果检验

3.4 脉冲响应检验

输出脉冲响应结果如图3所示。图3a为航班总量对航班总量的响应；图3b为航班总量对信道时间占用度的响应；图3c为信道时间占用度对航班总量的响应；图3d为信道时间占用度对信道时间占用度的响应。图3中蓝线为冲击响应曲线，红线为冲击响应的置信区间。

图3b表明了航班总量对信道时间占用度的随机扰动冲击所做出的动态反应，航班总量在信道时间占用度期望冲击2期开始上升，在第4期达到峰值，于第7期降为最低值，第7期后冲击逐步趋于平稳直至消失。这表明信道时间占用度产生冲击后，将在2～6期内对航班总量产生拉动作用，在7期之后冲击产生的拉动作用逐渐消失，即信道时间占用度对航班总量的扰动仅能存在一周左右。

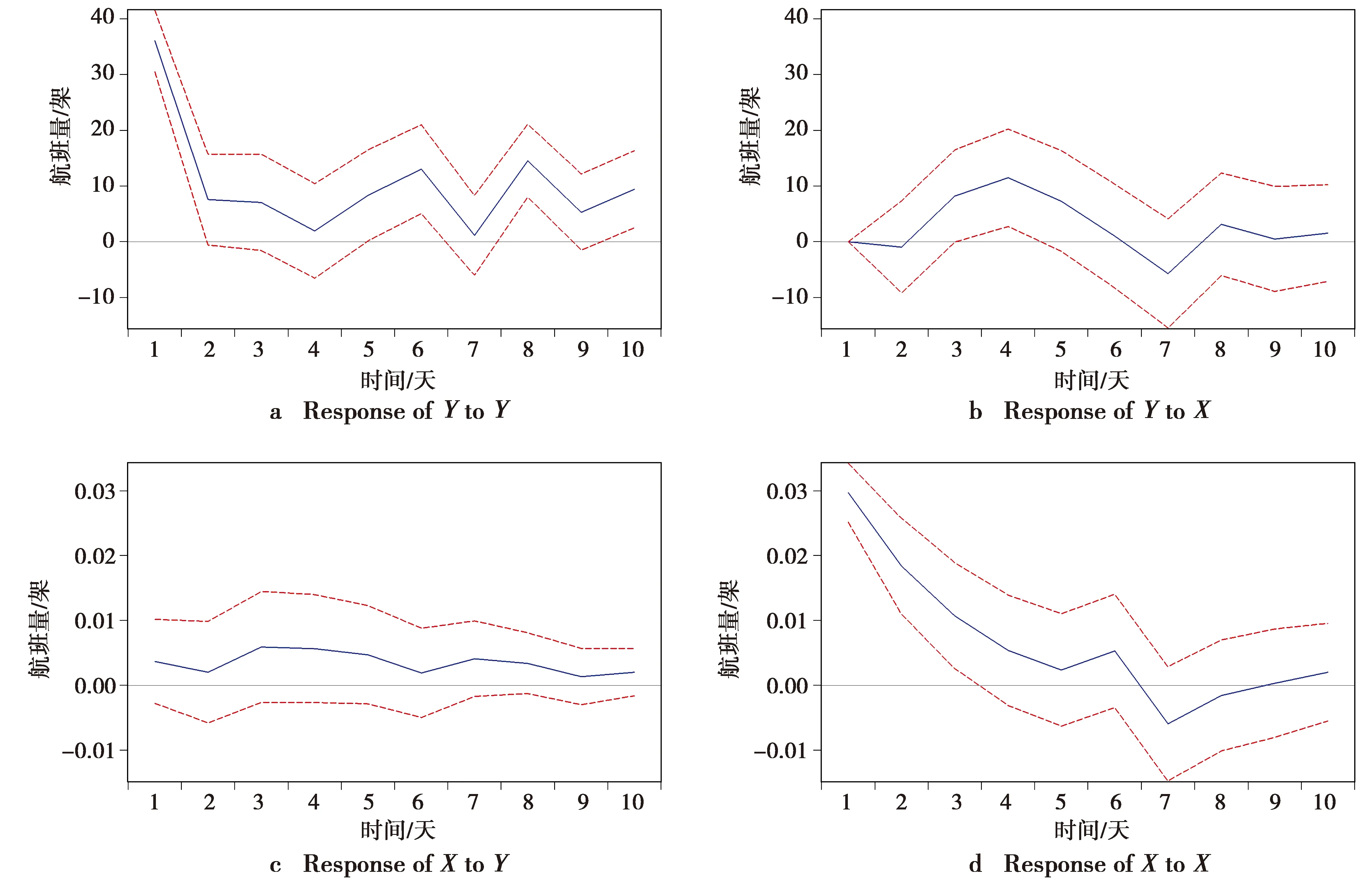
图3 信道时间占用度对航班的影响Fig.3 Influence of channel time occupation on flight

3.5 曲线拟合

使用对VAR模型进行修正后构建的VEC模型对航班量进行拟合后结果如图4所示。

图4 VEC模型的航班总量拟合效果Fig.4 Flights matching of VEC model

图4中蓝色实线表示航班总量的实际值，红色虚线表示构建的VEC模型产生的航班总量拟合值。对比航班拟合值和实际值可以发现，拟合曲线与实际曲线的趋势基本相符。且本次测试时间正处于航班受疫情影响从低谷并逐渐恢复的过程中，航班量从5月开始出现了明显上升，拟合曲线的增长趋势快速跟上了航班实际增长趋势，拟合曲线的效果良好。

3.6 预测结果对比分析

使用航班总量构建ARIMA(4，1，1)模型，对航班总量进行单变量预测较为合适，结果如表7所示。

表7 航班序列ARIMA模型阶数统计概率

分别利用上述构建的VEC(6)和ARIMA(4,1,1)对7月3日—7月11日航班量进行预测，结果如表8所示。

对比预测结果和实际航班总量可发现，2种模型预测结果在5天内相对误差范围在5%，往后几天预测误差波动较大，整体而言VEC(6)模型和ARIMA(4,1,1)模型预测的相对误差均控制在10%左右，但前者在平均误差、最大误差和误差方差方面均小于后者，与格兰杰因果关系分析一致，即信道时间占用度的引入有助于减少航班预测值方差，这表明信道时间占用度有助于提升航班总量预测精度。

表8 基于修正后VAR模型的航班总量预测

4 结束语

本文结合ITU及国家无线电管理机构相关测试标准和频谱占用模型相关理论，使用信道时间占用度和航班总量序列构建VAR模型进行关联性分析和预测，并将预测结果与ARIMA模型的预测结果进行对比分析，验证了时间序列分析应用于频率使用率分析的适应性，为利用航空甚高频频率使用率预测航班规律提供了参考，同时也为深度挖掘无线电频率使用率数据的应用价值提供了新思路。