基于高阶累积量和改进GRNN的CSI手臂行为识别

李新春，谷永延，黄朝晖，纪小璐，魏 武，孟 硕

(1.辽宁工程技术大学 电子与信息工程学院，辽宁 葫芦岛 125105；2.辽宁工程技术大学 研究生院，辽宁 葫芦岛 125105)

0 引 言

近年来，随着智能化科技的不断进步，人们日益增长的美好生活需要，对智能住宅，娱乐，安全健康检测等人机交互系统要求普遍提高。在未来智能机器人时代，利用手臂动作控制智能机器人成为人机交互系统中一项有着重大研究意义的工作。

基于加速度计[1]、陀螺仪和雷达[2]等特定传感设备的行为识别，存在穿戴繁琐、行动受限和高功耗等问题；基于视频图像行为识别[3-4]，存在隐私易曝光、照明要求高、高存储高成本等缺点。当前无线局域网络(wireless local area network，WLAN)已经覆盖到生活的各大场所[5]，为基于WiFi传感系统的行为识别技术研究创造了有利条件，所以基于WLAN的行为识别技术被广泛应用。

目前，一些研究利用接收信号强度(received signal strength，RSS)作为行为识别特征[6]，但是，RSS存在粗粒度、稳定性弱、鲁棒性差、较低识别率等缺点。相对而言，拥有细粒度、高频谱利用率、抗强多径干扰等特点的信道状态信息(channel state information，CSI)存在更高的感知精度和更稳定的感知性能，近年来基于CSI的人体行为识别技术成为研究热点[7]。

文献[8]对每个子载波的CSI幅度信息进一步提取方差特征并结合稀疏表示分类(sparse representation classification，SRC) 算法实现日常动作的识别。文献[9]利用主成分分析(principal component analysis，PCA)进行子载波的选择，克服了数据冗余的问题，并将所提取的特征输入到支持向量机(support vector machine，SVM)模型中进行识别。文献[10]提出的CARM系统建立了速度和活动2个模型，量化了人体活动与CSI之间的关系，最后通过log相似度计算进行分类。以上文献只依赖幅度信息，没有对敏感性更强的相位信息进一步研究，在识别精度上还有提升空间。文献[11]对幅度信息和经过线性变换后的相位进行相关性特征提取，并使用BP神经网络进行分类。文献[12]利用最大绝对偏差值进行子载波筛选，利用动态时间规整(dynamic time warping，DTW)对线性变换后的相位差进行模板分类，且训练大规模数据时，DTW降低了识别效率。在以上2种研究中，相位虽经过线性变换却忽略了非线性误差，且存在处理复杂度提升等问题。文献[13]对幅度相位进行功率谱熵的特征提取，并利用人工鱼群算法优化SVM模型进行识别分类。文献[14]利用小波变换提取信号的能量和方差特征，并用隐马尔科夫模型(hidden markov model, HMM)进行动作分类。文献[15]利用小波变换进行去噪处理再通过PCA算法提取特征值，并输入到训练好的随机森林(random forest,RF)模型中进行识别。文献[13-15]提取方差、功率谱熵和能量等二阶统计特征，并使用PCA和小波变换等线性分析工具，不能很好地捕获CSI数据中的非高斯和非线性信息，影响后期识别准确度。近两年，行为识别使用深度学习框架的研究也逐步开展，如文献[16]提出使用稀疏自动编码器(sparse auto encoder，SAE)从CSI数据中自动提取有用特征来进行动作识别，但是深度学习需要大量的样本数据来进行反复参数调整训练，以提高识别准确度，且对数据的解释性很差。

针对上述CSI行为识别中存在的问题，本文提出基于高阶累积量和改进GRNN的CSI手臂行为识别算法。该算法将CSI幅度和未经线性变换的相位差作为基信号，再通过改进的spearman rank相关系数对子载波进行选择，并提取其更深层的三阶累积量构建行为特征集，最后利用新型群智能优化的灰狼算法优化GRNN形成GWO-GRNN分类模型进行动作分类。本文算法训练参数少，减少了训练时间开销，鲁棒性强，有利于行为识别准确度的提升。

1 手臂动作与信道状态信息

1.1 CSI相关理论

CSI 值揭示了通信链路中的信道属性，可利用具有正交频分复用(orthogonal frequency division multiplexing，OFDM)技术的商用网卡Intel 5300 NIC将收发链路间子载波级的CSI提取出来[17]。其在频域内的信道响应可表示为

Y=HX+W

(1)

(1)式中：Y，X分别为接收和发射的信号序列；H为由复值数据组成的信道矩阵；W为随机噪声。

基于802.11n协议支持的MIMO技术，接收的CSI测量值矩阵表示为

(2)

(2)式中，T和R分别为发送和接收天线数目。

矩阵中Hij含有由文献[18]所提工具采集出的30个子载波，可表示为

Hij=[Hij1,Hij2,…,Hij30]

(3)

(3)式中，每个子载波Hijn被定义为

Hijn=|Hijn|ejsin(∠Hijn)

(4)

(4)式中，|Hijn|和∠Hijn分别表示第i发送天线和第j个接收天线的第n个子载波的幅度和相位。

1.2 手臂动作与CSI幅度

由于人体是发射信号的良好反射器，则在接收和发送设备间做不同手臂动作会产生不同强度和轮廓的CSI幅度波形图。图1为做拍手和抬臂2个不同手臂动作时引起的幅度波形图，呈现出明显不同的信号特性，表明了不同手臂行为与信号幅度的一一映射关系。

图1 不同动作的幅度波形图Fig.1 Amplitude waveform of different actions

1.3 手臂动作与CSI相位

针对直接采集的相位随机分布[19]无法直接使用问题，研究者通常对相位进行线性变换处理，但忽略了相位中存在的非线性信息。以下理论验证了相同子载波两天线间相位差的高度稳定性。

(5)

(5)式中：∠CSIi是真实相位；mi为子载波i的子载波索引；β为初始相位偏移；Z是高斯白噪声；λp,λs和λc分别是由分组边界检测，采样频率偏移和中心频率偏移引起的相位误差。因无法准确获得λp,λs和λc，故不能直接计算出真实相位。而Intel 5300无线网卡的3根天线使用相同的时钟和相同的下变频器频率，所以不同天线相同载波的分组检测延迟、采样周期、频率差和mi相同。则两天线上测量子载波i的CSI相位差可表示为

(6)

(7)

由(7)式可知，测量相位差的均值与原始相位差的均值差是一个常数，方差差只是噪声之隔的差距。因此证明了在接收端两根天线上相同子载波的相位差是高度稳定的。图2为拍手动作引起的相位和相位差波形图。

图2 拍手动作的相位和相位差波形图Fig.2 Phase and phase difference waveforms of clapping

2 子载波选择和高阶累积量特征提取

2.1 改进spearman rank子载波选择算法

对CSI原始数据计算出幅度和相位差后，若对所有子载波进行处理，会造成数据冗余，效率低下等问题，所以子载波的处理方式决定了能否高效、精准地进行行为识别。现研究通常有2种处理方法：①对所有载波进行平均处理[20]，会弱化动作对载波波动程度，造成细节信息的丢失；②选择平均绝对偏差最大的子载波[12]，会存在鲁棒性差等问题，两者都不能有效提高识别精度和效率。

由于平均绝对偏差(mean absolute deviation，MAD)可反应数据的分离程度的特性，可用于子载波对动作敏感程度的测量，MAD值越大子载波变化越大。spearman相关系数对数据错误和极端值的反应不敏感，适用范围广，可有效度量子载波间的相关程度。基于以上优势本文提出MAD改进spearman rank子载波选取算法，提高子载波信息的利用率。具体步骤如下。

1)利用(8)式计算各个子载波基信号的MAD，选取MAD值最大的子载波作为基载波p。

(8)

(8)式中：csii为子载波基信号的第i个数据；E(csi)为数据均值；N为数据包总数。

2)取载波p和其他载波q，其第i个数据值分别为pi和qi，并对其载波数据进行排序，得到pi和qi排序后的排名E(pi)和E(qi)。

3)将pi和qi的排名E(pi)和E(qi)进行相减得到排行差di=E(pi)-E(qi)。

5)依次循环，直到得到p载波和其他所有子载波的相关系数，根据相关系数大小排序进行较强相关性的子载波选择。

2.2 高阶累积量特征提取

子载波选择后，从所选子载波的CSI幅度和相位差数据中挖掘非线性深层次特征，对提高动作识别性能可以起到关键性作用。高阶累积量已经被成熟运用到各类信号分析中，如脑电信号、心电信号[21]。由于高斯信号具有高于二阶的累积量为零的特性，因此，高阶累积量可以很好地抑制加性高斯白噪声，对噪声和信号干扰具有很强的鲁棒性；含有二阶统计不易发掘的非线性特征信息，还考虑了幅值、相位信息，有利于提高信噪比和识别准确度。

假设CSI基信号时间序列为X(i)，时延参数为τ，E[·]为统计期望运算符，则各阶累积量的计算公式如下。

C1x=E(X(i))

(9)

C2x(τ1)=E(X(i)X(i+τ1))

(10)

C3x(τ1,τ2)=E(X(i)X(i+τ1)X(i+τ2))

(11)

C4x(τ1,τ2,τ3)=

E[X(i)X(i+τ1)X(i+τ2)X(i+τ3)]-

C2x(τ1)C2x(τ2-τ3)-C2x(τ2)C2x(τ3-τ1)-

C2x(τ3)C2x(τ1-τ2)

(12)

n阶累积量可由n阶矩导出如下。

Cnx(τ1,τ2,…,τn-1)=mgnx(τ1,τ2，…，τn-1)-

mgGNx(τ1,τ2，…，τn-1)

(13)

(13)式中：mgnx(τ1,τ2，…，τn-1)是第n阶矩；mgGNx(τ1,τ2，…，τn-1)是具有相同功率谱密度的高斯过程的第n阶矩。更高阶的累积量需要巨大的计算工作，因此，本文对CSI的幅度和相位差利用MATLAB集成的高阶谱分析(HOSA)工具箱进行三阶累积量非线性特征的提取。图3和图4分别为采集的拍手和抬臂2个手臂动作幅度数据的三阶累积量及其等高线，既揭示了等高图的对称性又验证了手臂动作可用三阶累积量特征进行明显区分。

图3 拍手动作的三阶累积量和等高线Fig.3 3 D cumulant and contour of clapping motion

离线阶段，对采集的平臂、抬臂、扔东西、弯曲、拍手、喝水6个手臂动作CSI数据进行幅度和相位差的提取和子载波选择，设选取载波个数为n1，并对所选子载波提取11个高阶累积量特征，则每动作每链路形成n1×11×2形式的特征集。

3 基于GWO-GRNN的动作识别模型

3.1 广义回归神经网络识别

动作识别模型是在子载波选择和特征提取的基础上建立的，是判断手臂动作类别的重要环节。GRNN是由The Lockheed Palo Alto研究实验室的Donald F. Specht在1991年提出的一种基于记忆且非线性的神经网络模型[22]，有很强的非线性逼近能力和容错性能，且学习收敛速度快，鲁棒性强。

图4 抬臂动作的三阶累积量和等高线Fig.4 3 D cumulant and contour of arm lift

GRNN由输入动作特征数据的输入层、利用高斯激活函数作为节点的模式层、对模式层输出处理的求和层和输出动作类别的输出层构成多层深度神经网络。结构框图如图5所示。

图5 GRNN框图Fig.5 GRNN block diagram

1)设变量x和y的联合概率密度函数为f(x,y),则y对于向量X的回归值为

(14)

(15)

(15)式中：n是样本总数；σ为光滑因子即高斯的宽度系数。

(16)

3.2 灰狼算法改进GRNN分类模型

GRNN仅有一个自由参数σ，如何确定最优化因子σ是GRNN网络训练结果优劣的关键。由于交叉验证[24]优化σ速度慢、准确度低，本文提出利用灰狼算法优化GRNN网络的关键参数(光滑因子)以提高网络识别性能，使得最终形成的GWO-GRNN动作分类模型能准确地映射特征集——动作的关系。

3.2.1 灰狼优化算法

灰狼优化算法是Mirjalili等[23]从野狼捕猎行为中受到启发，联想到的一种简单高效智能的群体优化算法。它具有操作简单、参量少、收敛搜索速度快等优点，适合优化GRNN模型参数，构成参数少、极易收敛的动作识别模型。

灰狼优化模型通过领导和被领导的机制完成捕猎行为得到最优参数。其中前3匹狼α，β和δ为狼群中的领导者(最优解)，γ为被领导群体(候选解)。

灰狼捕猎对应的严格数学建模优化步骤如下。

1)包围猎物。根据猎物位置更新灰狼在猎物周边的任何随机位置，并进行猎物包围。

(17)

(18)

(19)

(20)

(21)

2)狩猎。保存目前为止适应度最强的α，β和δ狼，在其带领下更新包含γ在内的其他狼的位置并进行猎捕。

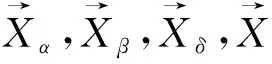
(22)

(23)

再根据(23)式表示出灰狼个体γ朝向α，β和δ逼近的步长和方向，最终由(24)式得到狼种群的更新位置,逐渐进行猎物捕获。

(24)

3.2.2GWO优化GRNN参数模型

GWO-GRNN模型流程图如图6所示。

本设计运用GWO对于广义回归神经网络的光滑因子进行优化。具体实施步骤如下。

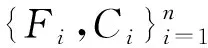
图6 GWO-GRNN模型流程图Fig.6 GWO-GRNN model flow chart

2)GWO算法初始化。设置狼群数量N，最大迭代次数tmax，初始化狼群的初始位置，确定优化参数的个数和取值范围。由于本文利用GWO优化GRNN的σ参数，则参数个数设置为1。

3)约束条件处理。遍历每个狼，使每个狼的位置都保持在σ参数的最小值和最大值之间。

4)计算适应度函数值。遍历每个狼，利用训练集进行GRNN模型的训练，并将测试集中每一手臂动作特征依次输入到模型，得到预测动作类别并计算手臂动作识别错误率fitness，将fitness作为狼的适应度函数值。

5)更新α，β和δ位置和目标函数值。在每次迭代中，以动作识别错误率fitness最小化为优化原则，选取适应度最强的3匹狼，对α，β和δ的位置和目标函数值进行更新。

6)计算参数A，C，a。根据(19)—(20)式计算相应的A，C值。

7)更新当前种群位置。在α，β和δ这3匹狼的领导下，利用(24)式更新狼种群的位置，逐渐逼近猎物。

8)迭代更新。增加迭代次数并判断灰狼算法是否达到最大迭代次数tmax。如果已经达到tmax，则最优狼α的位置即为最优参数。否则，跳回步骤3)继续循环迭代，直到达到最大迭代次数。

9) 完成识别模型构建。基于最优参数得到GWO-GRNN动作识别模型。

10)特征集建立。依据动作标签不同分别将相应动作数据分为训练集和测试集，进行模型训练和测试，得到相应标签动作特征集；在线测试时与输入的在线测试数据进行特征匹配，以实现手臂动作的识别。

图7给出了基于高阶累积量和改进GRNN的CSI手臂行为识别的流程。

图7 算法流程Fig.7 Algorithm flow

4 实验与结果分析

4.1 实验设置

为验证本文提出的行为识别方法性能，在学校实验楼选择一间大小为5 m×9 m，放有办公桌椅等物品的封闭办公室作为实验环境，并进行设备配置和数据采集工作。实验环境平面结构如图8所示。

图8 实验环境平面结构图Fig.8 Layout of experimental environment

在设备配置中，利用2.4 GHz频率的双天线TP-LINK WR842N路由器作为发射端(TX)，一台装有三天线Intel 5300 NIC网卡的DELL笔记本电脑作为接收端(RX)，并将两设备放置在高1.2 m的桌子上，相距2.1 m。然后将发射路由和接收设备进行ping命令连接，进行信号的收发，保证通信链路的畅通。在数据采集中，实验通过寻找4名实验者(2男2女)在收发设备间做平臂、抬臂、扔东西、弯曲、拍手和喝水6个不同手臂动作，每人每动作执行20次，取出5次作为测试集，通过身体的反射、折射和散射形成CSI动作数据，并通过装有Ubuntu Linux 10.04 LTS操作系统的电脑，利用Halperin等人开发的CSI TOOL提取内置网卡中的CSI动作数据，完成数据采集工作。

对本文所提算法的实验仿真都在MATLAB R2017b上进行编程实现。

4.2 基信号不同对实验的影响

为了验证选取不同的基信号对行为识别性能的影响，本文通过对比RSS值、幅度、相位和本文提出的融合幅度相位差4种不同基信号来验证不同基信号的选择对识别性能的影响。实验在相同环境下进行并对他们进行相同的后期处理，确保有效的对比性。在图9显示的对比实验识别准确度中表明，CSI的3种基信号的识别性能明显高于具有85.83%识别率的RSS数值，验证了CSI信号更稳定更具代表性。单一信号的幅度和相位相差甚少，由于融合幅度相位差的基信号比其他3种基信号含有更丰富的动作信息，因而其识别性能远优于单一的基信号，可达到95.83%的识别准确度。结果表明，本文所提相位差与幅度的融合更能稳定地反映手臂动作情况，提高动作指纹的可靠性，得到更高的识别准确度。

图9 不同基信号识别准确度Fig.9 Recognition accuracy of different base signal

4.3 子载波选择设计

子载波选择的方法，影响着实验的识别效果。同样合适地选择子载波个数，既能减少计算量，又能达到理想的识别准确度。图10显示了抬臂行为的CSI幅度数据中一根天线中所有子载波的MAD值，可以看出第2个子载波MAD值最大。本文再通过此基信号，得到其他子载波与此基信号的相关系数情况。并通过多次实验得出根据相关系数大小排列选取相关性较强的3个子载波可以得到更好的准确度。

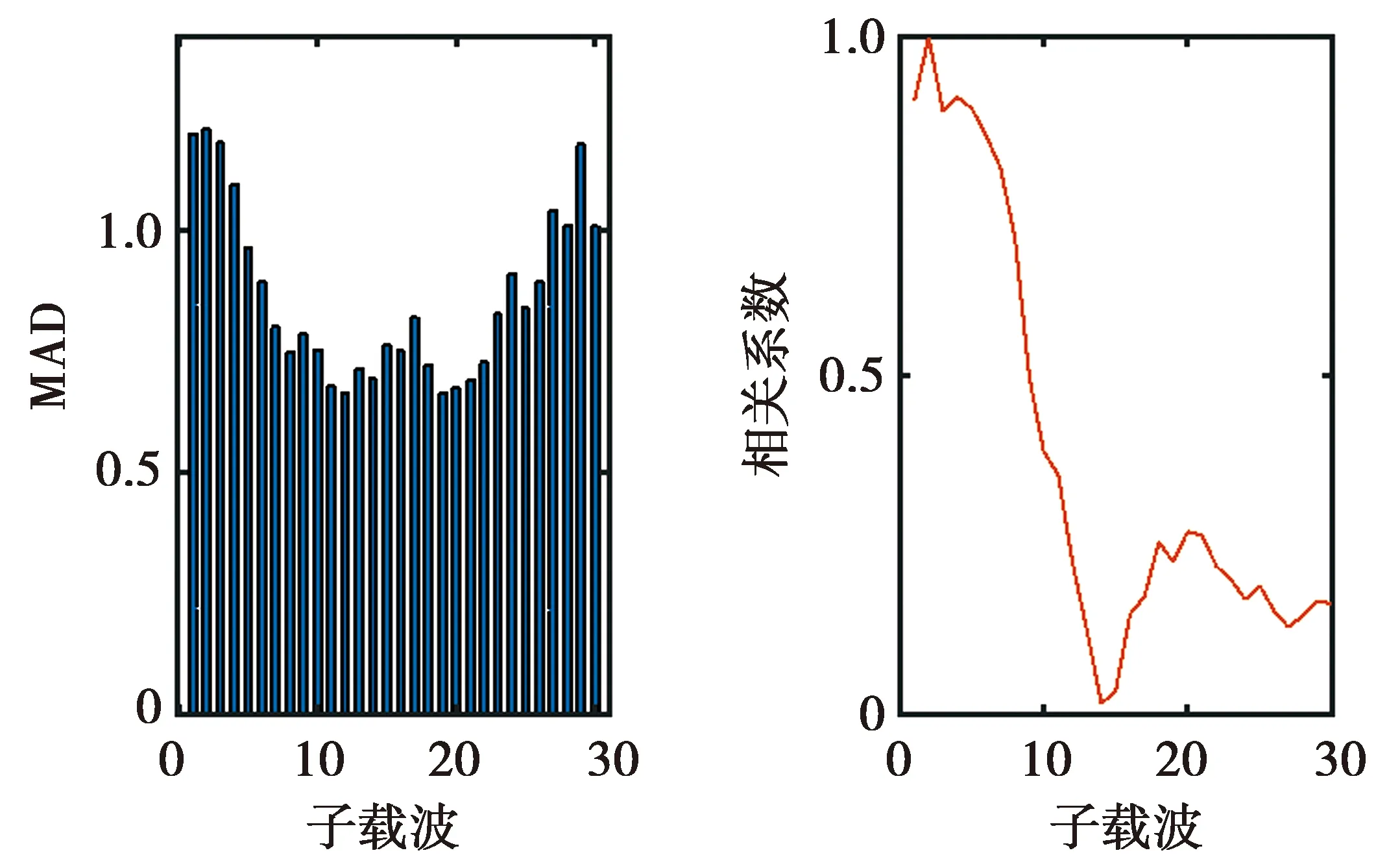
图10 子载波的MAD值和相关系数Fig.10 MAD and correlation coefficient of the subcarrier

4.4 子载波选择性能的对比

为证明本文所提子载波选择对动作识别性能的影响，本文实验分别与计算所有子载波平均值的方式一、选取平均绝对偏差值最大载波的方式二和利用所有子载波的方式三进行载波选择方式性能对比。图11显示了不同子载波选择方式识别准确度。从图11可知，本文提出的改进spearman rank子载波选择算法因包含更加全面的子载波动作信息比前2种子载波选择方式高出6%和4%的准确度，由于方式三含所有载波信息，故本文子载波选择方式的识别精度略低于方式三，但在相差甚少的1%基础上，本文方式用很少的计算时间，就可以达到理想的动作识别性能，更具子载波选择价值。

图11 不同子载波选择方式识别准确度Fig.11 Recognition accuracy of different subcarrier selection modes

4.5 优化算法的对比

为验证本文所提GWO算法在优化GRNN模型过程中具有良好的收敛速度和识别性能，与典型的粒子群算法和模拟退火算法分别优化的GRNN模型进行实验对比。本文将以上3种智能优化算法中种群数N设为60、最大迭代次数tmax设为 50，来增强实验的说服力。表1显示了以上3种优化模型的识别精度和相应的平均执行时间。图12显示了3种优化算法的迭代次数和适应度之间的对应关系。可知GWO-GRNN模型和SA-GRNN模型在收敛性能上明显优于PSO-GRNN模型，但在适应度相同的情况下灰狼算法表现出更快的收敛速度，且最终GWO-GRNN模型获得了更小的稳定适应度低于其他2种模型4%和2%。表明灰狼算法获得了更优的σ参数，在快速的收敛性能下，缩短了执行时间的同时提高了一定的动作识别准确度。

表1 优化模型的σ值和平均时间

图12 不同模型的优化过程Fig.12 Optimization process of different models

4.6 行为识别算法的对比

为了验证本文所提算法模型的识别性能，将所提HOC+GWO-GRNN算法模型与以下特征+分类模型的行为识别方法进行对比：高阶累积量+广义回归神经网络的(HOC+GRNN)模型、高阶累积量+灰狼优化的支持向量机的(HOC+GWO-SVM)模型、文献[8]中所提Var+SRC模型、文献[15]中的PCA+RF模型。为了保证对比算法在识别精度方面具有可比性，均在相同动作数据集(即本文所采集的手臂动作数据)、相同预处理的基础上进行实验验证。

图13为不同方法的识别准确度。由图13可知，在提取相同的高阶累积量的条件下，具有GWO参数优化操作的GRNN识别率明显高于GRNN模型，SVM对大数据存在局限性，通过GWO算法进行参数的优化，虽提高了一定的识别准确度达到92.91%，但依旧劣于本文算法。PCA算法对CSI数据进行主成分特征提取更凸显动作信息，识别精度比Var+SRC方法高出3%。本文所提高阶累积量含有文献[8]和文献[15]所提方差特征和经PCA提取特征所缺失的非线性特征，含有更细微丰富的动作特征信息，并利用GWO-GRNN模型提高收敛速度，使得平均动作识别率达到95.83%，高于所对比算法精度，有效提高了行为识别准确度。

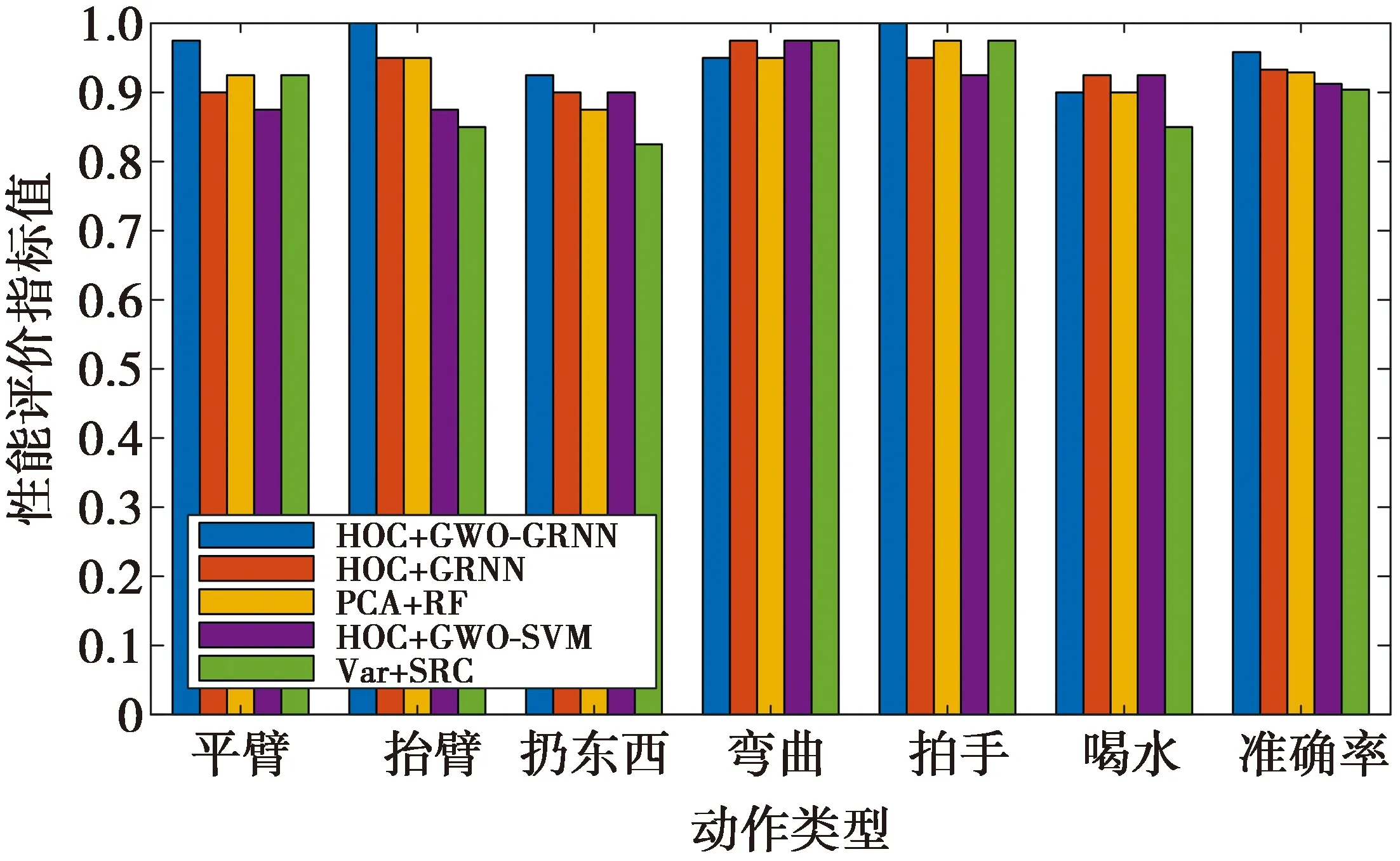
图13 不同方法的识别准确度Fig.13 Recognition accuracy of different algorithms

5 结束语

为了挖掘更有效更深层的动作特征，解决复杂环境下动作的识别准确度低的问题，本文提出基于高阶累积量和改进GRNN的手臂行为识别算法。实验结果表明，利用幅度+相位差作为基信号识别性能优于单一基信号和RSS数值。该算法利用MAD改进的spearman进行敏感性强的子载波选择，在保证较高识别性能的同时，提高了子载波信息的利用率，减少了计算时间开销。同时提取具有非线性特性的三阶累积量特征。此外，利用具有参数少、操作简单、收敛快的GWO算法优化GRNN参数形成GWO-GRNN动作分类模型，在收敛速度和识别准确度方面均优于SA-GRNN，PSO-GRNN模型。最终，该特征提取+识别模型方法使其在识别准确度方面优于HOC+GRNN、PCA+RF、VAR+SRC和HOC+GWO-SVM识别方法，验证了本文方法的可行性和研究价值。但是本文研究得还不够深入，当多人在室内杂乱运动时，很难判断单人的手臂动作类型，在后续工作中，要探寻能解决更复杂情况的手臂行为识别方法。