激光抛光熔化机制中表面形貌的数值模拟

徐辑林，邹 平，王文杰，康 迪，刘清泉

（东北大学机械工程与自动化学院，辽宁沈阳110819）

现代制造业的快速发展对材料表面质量提出了更高的要求，激光抛光技术作为一种非接触表面抛光技术，在近年来得到了迅速发展。目前，激光抛光主要有三种加工机制：熔化机制、过渡机制和烧蚀机制。在熔化机制中，激光抛光的能量密度不是很高，导致温度超过材料的熔化温度但达不到汽化温度，因此工件表面的材料只是被熔化和重布；在烧蚀机制中，激光抛光的能量密度足以使温度瞬间达到材料的汽化温度，直接去除一薄层材料；过渡机制介于熔化机制和烧蚀机制之间，既存在着材料重布又包含材料的去除。

在激光抛光的研究中，一些学者对激光抛光模型的发展起到了重要的推动作用。Ramos等[1]发现了激光抛光的两种工艺模式：浅层表面熔化和表面过熔化，并尝试建立激光抛光的数学模型，得到了满意的结果。Perry等[2-4]分析了激光抛光中工件表面形貌的空间频率，提出了一种能预测工件抛光后表面粗糙度的空间频率方法；然而，由于该法只考虑了熔池中的毛细力对表面形貌的影响，故仅适用于处于浅层表面熔化模式的激光抛光。考虑到热毛细力的影响，Ma等[5]将传热和流体流动耦合起来，建立了二维瞬态轴对称模型来模拟熔池表面轮廓的演化，然而该模型仅考虑了热毛细力，忽略了毛细力的作用。Zhang等[6]建立了考虑熔池毛细力和热毛细力的二维数值模型，揭示了毛细力和热毛细力的作用：毛细力可消除大曲率的表面凹凸不平，而热毛细力可提高抛光效率。到目前为止，通过激光抛光的数值模型来预测工件的表面粗糙度仍是一个难题。本文主要研究熔化机制下激光抛光表面形貌的数值模拟，试图建立一个数值模型来预测激光抛光熔化机制下被抛光工件的表面粗糙度。

1 数值模型

1.1 模型假设

在激光抛光的熔化机制中，主要涉及两个物理场：热场和流场。因此，本文建立了耦合传热和流体流动的二维移动数值模型来研究激光抛光的熔化机制。为了简化建模过程，做出以下假设：①熔池中的流动被认为是不可压缩的牛顿层流；②被抛光材料被认为是各向同性和均质的；③激光热源被认为是表面热源[7]。

1.2 模型的初始表面轮廓

建立长1800μm、高500μm的几何模型，建立直角坐标xoy，如图1所示。模型的初始表面轮廓对预测激光抛光后的表面轮廓和表面粗糙度非常重要[8]，本文中模型的初始表面轮廓（图1所示从x=0~1200μm）直接来自样品未抛光的表面轮廓，其表面粗糙度为Ra1.345μm。

图1 计算域示意图

1.3 传热

激光抛光中工件的传热表达为：

式中：ρ为密度；T为温度；t为时间；k为导热系数；Ceqp为等效比热容，定义为：

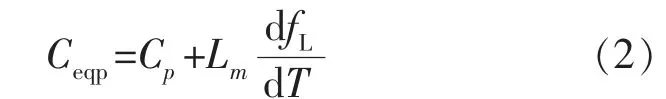
式中：Cp为热容；Lm为熔化潜热；fL为液体分数，定义为：

式中：TS为材料的固相线温度；TL为液相线温度。

图1所示边界2的边界条件表达为：

式中：α为材料的吸收率；h为自然对流系数；ε为辐射率；σ为Stefan-Boltzmann常数；Tamb为环境温度；I为具有高斯分布的激光热通量，定义为：

式中：P为入射激光功率；rb为激光束在工件表面的半径；vscan为激光束的扫描速度。

图1所示边界1和边界3的边界条件表达为：

图1所示边界4被认为绝热，表达为：

1.4 流体流动

熔池中的流体流动由质量守恒和动量守恒控制，表达为：

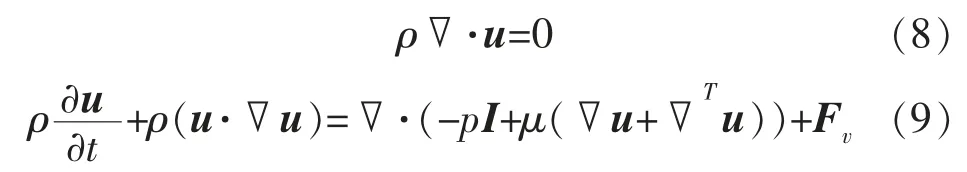
式中：p为压力；I为单位矩阵；μ为动力黏度；Fv为体积力，定义为：

式中：Fg为重力；Fb为浮力；β为热膨胀系数；Tm为熔化温度；g为重力加速度。

边界1、边界3和边界4被认为是无滑移壁，边界2为自由变形的表面，主要考虑表面张力在该表面的驱动作用，包括作用在熔池表面法向方向上的毛细力和作用在熔池表面切向方向上的热毛细力，该边界条件表达为：

式中：n为单位法向量；▽t为表面梯度算子；γ为表面张力，定义为：

式中：γm为纯金属在熔化温度下的表面张力；Aγ为表面张力梯度的常数。

1.5 数值求解

采用有限元法求解该模型，工艺参数为vscan=40 mm/s、P=250 W、rb=300μm。以304不锈钢为试验材料，在激光抛光模拟过程中，激光热源沿几何模型的上表面（边界2）以给定的扫描速度从x=0移动到x=1200μm，然后停止加热，模型进入冷却状态，温度逐渐降低到环境温度。

2 结果与讨论

2.1 熔池的演变

在激光抛光过程中，熔池随激光束在模型表面运动，在毛细力和热毛细力（Marangoni力）的作用下在模型表面重新分布熔池，使粗糙的工件表面变光滑。图2显示了t=5~35 ms激光抛光熔池的演变。在加热阶段，随着时间推移，熔池温度逐渐升高，熔池内的流体速度也逐渐增大。而由Marangoni力引起的Marangoni漩涡在熔池中形成，将熔池中心较热的物质输送到熔池边缘，导致熔池中心由于材料损失而出现凹谷（图2a～2c）。图2d显示了冷却阶段的熔池，其中仍存在Marangoni漩涡，但熔体流速较低，导致熔池表面轮廓基本固定，形成凹谷。

图2 模型中熔池的演变

分析可知，激光抛光过程中熔池中的Marangoni力始终是熔体流动的主导因素，影响熔池的表面轮廓，甚至影响工件抛光后的表面轮廓。

2.2 表面形貌和表面粗糙度

图3显示了激光抛光过程中表面轮廓ys的演变，可见被抛光的表面轮廓明显比初始表面轮廓平滑。然而，如前所述，在Marangoni力的作用下，激光热源下方的表面轮廓会形成一个凹谷，从而影响表面质量。

图3 模型中表面轮廓的演变

为了评估激光抛光试验中被抛光工件的表面粗糙度，计算出模型被抛光表面轮廓的表面粗糙度为Ra0.722μm。图4是抛光试验前后的工件表面形貌对比，工件的初始表面粗糙度为Sa1.403μm，激光抛光后的表面粗糙度为Sa0.845μm，与模拟结果Ra0.722μm非常接近。

图4 实验中工件的表面形貌

2.3 被抛光表面轮廓的形成机理

在激光抛光过程中，激光束在工件表面以扫描速度vscan移动，材料熔化，形成熔池。熔池前端的材料不断熔化到熔池中，而熔池末端的材料继续凝固形成新的表面。在熔池末端有一个气相、液相和固相交汇的位置，称为三相点（二维）或三相线（三维），由于本文建立的模型是二维模型，所以这里称之为三相点。三相点的运动决定了激光抛光后工件的表面轮廓，其运动可用熔池表面的凝固角θs来表征，如图5所示。θs与激光抛光后工件的表面形貌直接相关：θs>0，三相点向上移动；θs=0，三相点水平移动；θs<0，三相点向下移动。

图5 凝固角的定义

图6描述了凝固角θs对抛光表面轮廓ys的影响。可见，凝固角值的正负决定了抛光表面轮廓是上升还是下降，凝固角值的大小影响抛光表面轮廓的上升或下降速度。结合图2所示的熔池演变，可发现由Marangoni力引起的Marangoni涡旋是影响凝固角演变的主要因素。

图6 凝固角对抛光表面轮廓的决定性影响

综合以上，激光抛光熔化机制中被抛光表面轮廓的形成机理表现为：①激光与材料的相互作用使材料熔化，形成熔池；②在表面张力作用下，熔池中的熔体形成Marangoni涡旋；③熔体流动影响凝固角的演变，凝固角的演变直接决定抛光表面轮廓的形成。

3 结论

为估算激光抛光熔化机制下工件抛光后的表面轮廓，本文建立了耦合传热、流体流动和工件初始表面形貌的二维移动数值模型，得到以下结论：

（1）利用该模型对熔池的演化过程进行了数值模拟，表明Marangoni力控制着熔池中的熔体流动。

（2）测算抛光后工件的表面粗糙度，与预测数值进行对比，表明模拟结果与试验结果非常接近。

（3）引入凝固角的概念，揭示激光抛光熔化机制下被抛光表面轮廓的形成机理，表明凝固角的演变最终决定了激光抛光后工件的表面形貌，这是激光抛光过程中的一个关键参数。