基于深度学习理念的数学单元教学设计

刘春换 杨亮

【摘要】基于“深度学习”的高中数学单元教学设计从确定数学单元主题、单元结构构建、单元课时设计的策略三个方面展开，以“任意角和弧度”单元课例，进行深入探讨和分析，其目的在于提升高中数学单元设计效果，提升高中数学教学效果，旨在为相关研究提供参考。

【关键词】深度学习;高中数学;单元教学

单元教学是在整体思维指导下，从提升学生核心素养的角度出发，通过课时教学的落实，培养学生身心全面发展的教学理念，虽是以单元为模块，但是在课时教学时却是多元化的。新课改实施以来，如何将新课改理念深入到教学实践并凸显学生主导地位，促使学生深度学习，是很多一线教师日常研究的问题，那么“教学设计”作为教师日常工作的一部分，对于新课程理念的实施及教学工作的开展起着至关重要的作用。在教学实践中如何进行单元设计，促进学生深度学习呢？在此以“任意角和弧度”的单元教学为例进行说明。

一、基于知识的整体性确定数学单元学习主题

单元主题的确立要注重以核心素养为基础，以整体思维为导向，将数学教材内容进行有效划分以及重组，分配好课时内容，每个单元至少要包含一个数学核心素养，学习存在一定的梯度，体现出数学学科思想方法，以及认识世界的主要方式。只有通过此种形式确立的数学单元主题，才更符合学生的认知和发展规律。学生能够在新单元的“整体关联性”中了解知识的来龙去脉，深度参与到课堂学习过程中。在新课学习阶段，教师可以将一个完整的主题划分为几个不同单元主题进行学习，例如“任意角和弧度”这一单元，以往的教学中，许多一线老师将“弧度制”和“任意角”这两个知识点割裂开来教学，导致学生对“弧度制”这一知识点理解不够透彻。究其根本原因在于学生不了解这两个知识点的上下位关系：弧度制是任意角的一种度量单位。因此笔者以“整体思维”为导向，将“任意角和弧度”作为一个单元进行教学。通过此单元教学过后，在笔者设计了学生调查问卷，针对问题“你认为弧度制和任意角之间的关系是：_________”，百分之八十的学生能说出弧度制是任意角的一种度量单位。说明通过单元整体教学后，学生对这一知识的理解比较深入。

二、以数学对象研究的基本套路为主线明确单元结构构建

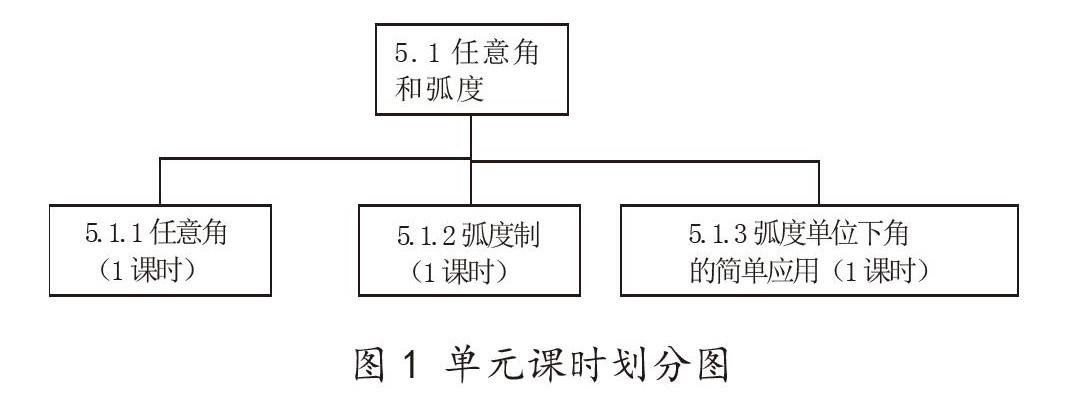
数学研究对象在变，但是研究的套路不变，数学的思想方法不变。因此教师在单元备课过程中，要看到教材的“明线”“暗线”。所谓明线：事实—概念—性质—结构—应用，暗线：事实—方法—方法论—本质观。而明暗线的结合“背景（一类事物的实例）—概念（研究对象）—性质（要素、相关要素之间的关系，变化规律等）—结构（相关知识的联系）—应用”这个过程就是在教学中落实了核心素养。我们在教学中要经常问自己用了什么数学方法定义了概念。例如函数的概念是语言与工具的学习，教学的过程应体现语言工具学习的特点：先模仿后归纳、应用。因此，函数教学的基本路径应为：背景—概念—性质—应用。掌握了数学研究对象的研究套路后，对本单元的课时结构安排就明确了。例如笔者将“任意角和弧度”这一单元的课时划分如图1：

三、单元设计中的课时教学要凸显学生的主体性

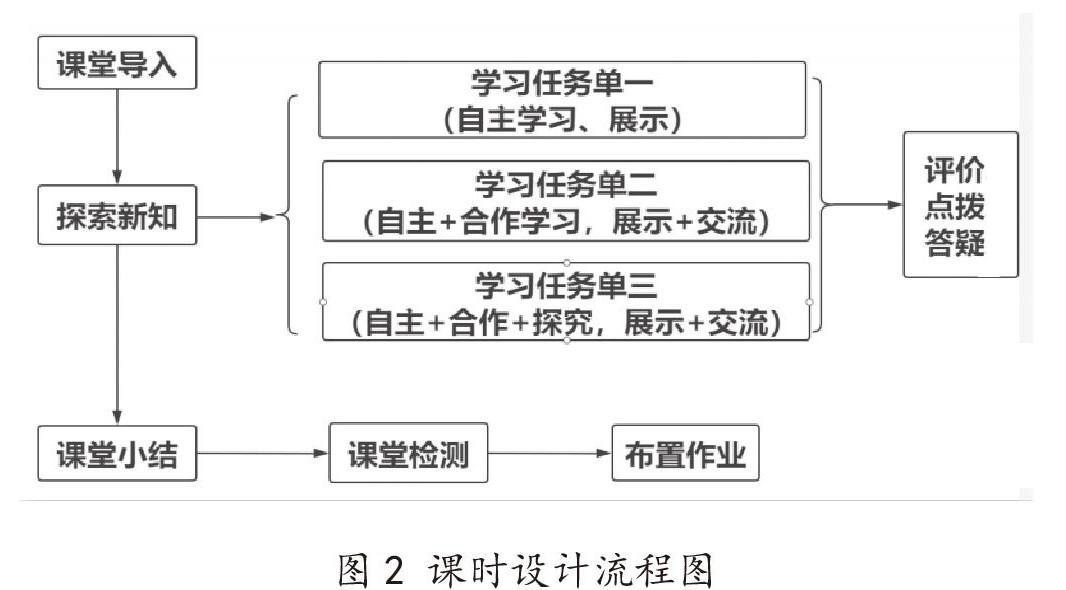
单元教学虽是以单元为模块，但是课时设计却是多元的。教师在课时设计上落实深度学习教学实践至关重要。教师在课时的设计上应以学生的主导地位为主，让学生积极主动参与到课堂中，学会发现问题、提出问题。单元教学的课时设计需要按照学生学习目标为基础确立课堂任务、评价任务和作业，使得教师在教学过程中真正体现教、学、评价的一致性。简而言之，深度学习下的单元课时教学课堂应该是情境+问题。笔者和课题组成员归纳了课时设计应该包括的流程，如图2：

四、课时教学设计案例展示

单元教学设计的目标是通过每一个课时来实现的，因此每个课时的教学设计是单元教学目标达成的基石。笔者根据单元教学策略，以问题导向为载体，简单展示“任意角和弧度”的第二课时“弧度制”这一节课的部分课堂设计。

1.回顾旧知，类比引入。

问题1：亚洲飞人刘翔打破了110米跨栏的世界纪录，110米换种说法为0.11公里，这种说法正确吗？为何两组数值不同？

师生活动：教师引导学生思考为何两组数据不同，学生马上明白是因为采用了不同的单位制，而且不同的单位之间可以换算。

问题2：初中所学的弧长公式有点繁琐，学习了弧度制后，弧长公式会变得简单许多，各位同学相信吗？

师生活动：教师设疑，学生引起对弧度制的求知欲。

2.合作探究，建构概念。

引导语：实践出真知，让我们一起探索数学的奥妙吧！请同学们动手完成实验一。

问题3：（实验一）

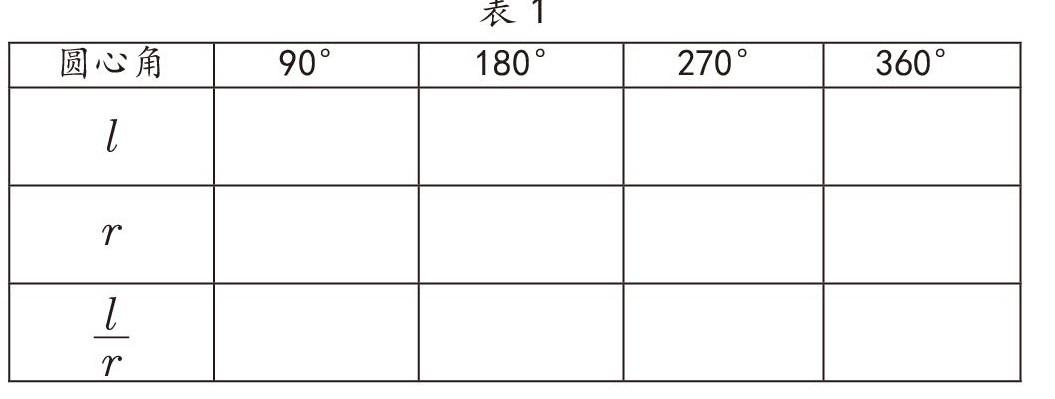
（1）请同学们在自己的圆上，分别作出圆心角为90°、180°、270°、360°。

（2）计算对应的弧长l1，弧长与半径的比值。完成下列的表1。

（3）小组合作讨论，你们有什么发现。

师生活动：学生很快作出90°、180°、270°、360°这四个角，并利用直尺量出各圆的半径，并计算出对应的弧长，求出弧长与半径的比值。通过小组合作讨论发现问题：

（1）同一个角，在不同的圆内，半径不同弧长不同，但是相同。

（2）当圆心角不同时，也不同。

追问：同学们非常棒，刚才我们取的是几个特殊角，那么对于任意角呢，这样的结论适用吗？

（教师展示GGB动态演示：随着圆心角的确定，弧长与半径的比值也随之确定，如图3）

4.生成概念，动手感知。

引导语：在二百多年前，瑞士数学家欧拉和数学教师汤姆生共同提出用弧长与半径的比值来

度量角。∠弧度弧度，特别地，时，∠AOB=1弧度。

我们规定：长度等于半径的圆弧所对圆心角叫作1弧度的角，单位为rad。

问题4：（实验二）那么现在你能根据定义在你的圆上做出1弧度的角吗？并与你的小组交流1弧度角的画法。

师生活动：学生很快就做出了1弧度的角，但是有些学生容易忽略1弧度角的方向。

问题5：（实验三）比较小组内的1弧度角的大小，说说你的发现。

师生活动：比较后发现果然两个1弧度的角大小一样。师生共同得出结论：无论是角度制还是弧度制下，角的大小都和半径的大小无关。在半径为1的单位圆中，弧长为1所对的圆心角就为1弧度。在半径为1的圆中，圆心角的弧度数与所对的弧的长度是一致的，没有弧度数，能出现这样的奇迹吗？（学生因数学的奇异美妙而发出惊奇兴奋的呼声）

问题6：根据概念我们已经知道当弧长是半径的1倍时，所对圆心角的弧度数为1弧度;当弧长是半径的两倍时，所对圆心角为2弧度，那么弧长l、半径为r，那么这条弧所对的圆心角a为多少弧度？

师生活动：教师引导，学生很快就能由刚才的

探究活动得出：。有些同学已经偷偷写成了。

追问2：在前面的学习中，我们知道角有正角、负角、零角。而我们弧长和半径都是正数。那么我们应该将弧长公式修改为什么？

师生活动：教师引导后，学生恍然大悟，马上

将弧度公式写成。

总而言之，深度学习对于数学教学发展存在一定价值。因此，教师要有效掌握此种教学理念，将其应用到教学过程中。深度学习在单元设计过程中首先需要教师及时转变立场，将教师需要做什么转变为要求学生做什么的思想上，引导学生思考、探究、回答问题，和亲自动手操作。还要转变教学视角，从关注教什么、如何教转向为关注学生为什么学、学什么、怎样学层面上，将评价作为教师教学决策和质量的主要依据。还要做好单元设计工作，强化不同数学知识之间的系统性，将其合为一体，注重结合实际生活，创设真实情境，提高学生解决问题能力。与此同时，教师还要高度重视，引导学生做好课后反思，培养学生批判性思维，提高学生深度加工能力，将知识转变为素养。

【参考文献】

[1]杨晓翔.高中数学教师单元教学设计现状的调查研究[J].江苏教育研究，2016（28）.

[2]魏强.新课改高中数学单元教学设计的实践探[J].数学教学研究.2017（02）.

[3]丁小红.把握深度学习本义，促进核心素养培育—以高中数学学科教学为例[J].数学教学通讯，2018（33）.