基于数字孪生视角的商业银行风险定价决策探析

吴永飞 孙静 王彦博 曹然 杨璇 刘曦子 史杰 张军 徐奇 王杰

摘要：  银行是经营风险的机构，如何形成有效的风险定价策略是各家商业银行不得不面对的重要经营问题。基于数字孪生视角，面向各类宏观因子变动下的风险情景，对商业银行资产负债管理体系进行仿真模拟，通过构建数字孪生仿真系统，推演出不同风险定价策略下银行未来经营收益情况，以期为银行风险定价决策支持提供借鉴。

关键词： 仿真模拟;风险定价;决策支持;商业银行;数字孪生

0 引言

银行是经营风险的机构，长期以来，商业银行在对企业和个人非系统性风险的防控方面积累了丰富的经验。然而，面对全球经济周期轮动、利率周期波动、货币政策的影响等系统性风险的冲击，商业银行仍缺乏相应的应对策略[1]。当前新冠肺炎疫情席卷全球，美国货币超发，全球金融市场动荡升级，系统性风险发生概率与日俱增。在此背景下，如何进行有效的风险定价，使银行在受系统性风险影响的情况下能够对风险进行有效管控并实现良好综合收益，已成为业界关注的重要课题。

银行的传统风险定价模型主要为成本加成法和基准利率法，但这两种方法都难以应对系统性风险对商业银行经营的冲击和影响，如果利用数字孪生技术仿真模拟银行给出定价策略后其面临系统性风险时的经营情况，就可以通过在数字孪生环境中反复输入多种定价策略来比对未来可能产生的多种经营收益结果，从中挑选最佳定价策略应用于现实环境，进而更好地应对系统性风险。

数字孪生技术通过对真实世界构建一个仿真的系统实验环境来预测系统的性能和参数，模拟一些真实世界中危险的、不可重复的实验，从而有效降低在真实世界中进行业务操作的成本[2]。一般说来，使用仿真模拟可以解决的问题包括：不易被人们看透的复杂系统问题、从大量方案中比较选优问题、存在危险现象的问题、实验成本过高或无法重复实验的问题等。商业银行在不同风险环境下的“经验”是一个极其复杂的系统，一旦出现策略失误将给银行带来不可逆的重大经营损失。因此，该场景适用于通过仿真模拟技术构建数字孪生环境形成解决方案。

1 面向银行风险定价的数字孪生环境构建

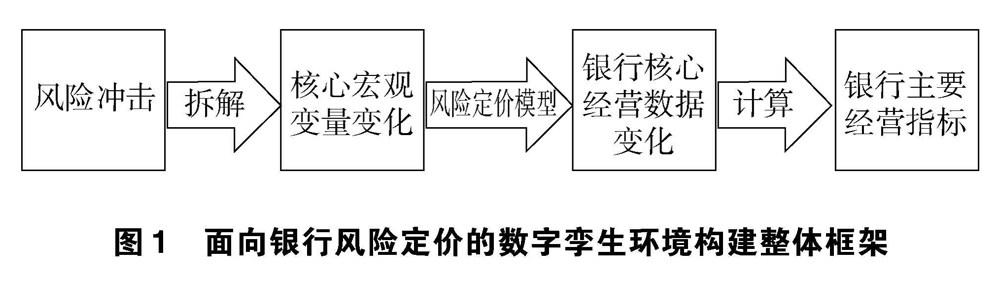
为了准确模拟商业银行的经营情况，需要结合不同风 险场景，模拟出银行在不同定价策略下资产负债表的变化情况，进而推演出银行在不同风险场景下的风险和收益情况。不同的风险冲击主要与宏观因素相关，银行资产负债表的变化主要与利率定价和风险环境有关。所以，模拟的关键在于如何构建从宏观因素端到商业银行资产负债端的业务传导逻辑，整体框架见图1。

1.1 风险冲击的数字孪生环境构建

第一，将风险冲击拆解成13个宏观经济变量，见表1。宏观变量的选择来自美联储压力测试模型，并根据我国具体情况有所调整。将历史上包括1998年亚洲金融危机、2008年全球金融危机在内的58次经典经济及金融市场风险案例拆解为主要宏观经济变量的变化，同时对数据进行处理，将变量的变化大小压缩在一年内，便于模型的模拟和对比分析。

第二，通过定价模型和风险模型分析宏观经济变量对于银行经营情况的影响。其中，定价模型表示根据不同资产类型的定价特点（如交易流程和价格敏感度 等），结合商业银行的定价，以及宏观经济指标的变化和对手银行的定价策略，计算各银行资产负债情况;风险模型则从“定价模型”模块获取各類资产负债当期 增量（也可能是削减，如触发资产证券化）、增量的价格，同时根据增量的价格、宏观经济指标变化（包括利率变化），以及自身的资产负债特征，计算风险损失以及相关的现金流（利率收入、利率支出、到期本金和提前支取等）。风险冲击主要影响银行的资产和负债，下文具体叙述银行资产端和负债端的数字孪生环境构建。

1.2 银行资产端的数字孪生环境构建

对资产端来说，银行最主要的资产就是贷款。贷款市场整体供应量同样会受宏观经济的影响，而银行每一项贷款的增量情况则根据银行自身的定价策略受不同宏观经济指标的影响。贷款的存量情况则根据原有合同的到期情况和对贷款提前还款情况的预测得到。另外，宏观经济情况会影响贷款的整体质量，通常采用以PD&LGD（多类别逻辑回归+迁徙矩阵模型）为基础 的资产信用风险模型来分析资产质量情况。

在银行资产端的数字孪生环境构建中，主要包括对4个模型的构建：市场供应量模型、贷款增量模型、资产信用风险模型、资产提前还款模型。

1.2.1 市场供应量模型

该模型在考虑“银行间的资金拆入、拆出”的基础上，聚焦宏观经济指标变化导致市场客群的资产负债需求总量变化。该模型的影响因子包括宏观经济指标和假设市场原有供应量等。

为最大限度地精准构建商业银行数字孪生环境下的我国整体市场贷款供需关系及潜在宏观经济变化对其造成的影响，通常考虑以区域、贷款类型作为划分维度，以历史信贷需求量作为因变量，以国家级、省级宏观经济指标作为自变量，并运用多元线性回归方法进行模型构建。

运用上述方法，按照贷款类型、区域维度，共生成146个多元线性回归子模型，大部分模型呈现出较好的拟合度及预测准确性。

在贷款类型维度，以全国银行商业房地产贷款实际发生量模型为例，模型整体的历史拟合及抽样测试都具有较高的准确性，见图2。

在区域维度，我国西北部经济欠发达省份的建模效果相对较差，整体信贷增量水平受宏观经济指标的影响也更不确定。

在模型整体的自变量贡献度方面，146个子模型中GDP （全国+区域）、M2（广义货币）和CPI为贡献度最高的因子，见图3。

在146个子模型中，最终根据R2、调整后R2、MAPE、RMSE等指标进行模型拟合度分析，遴选出72个子模型录入整体银行风险定价数字孪生框架中的市场供应量模型库，被录入的模型会在模拟发生不同虚拟风险场景下对整体市场的贷款供应量进行仿真计算。

1.2.2 贷款增量模型

该模型根据银行自身的定价策略、市场供应量模型及宏观经济指标对以贷款为代表的资产增量情况进行推演。同时，模型会参考贷款集中度的硬性指标。该模型的影响因子包括资产价格灵敏度、对手银行定价策略、银行自身定价策略、市场供应量模型和贷款集中度等。

整体贷款增量建模方法与上述市场供应量模型保持一致，沿用了多元线性回归技术。但在该模型中，对客户的资产价格灵敏度进行了较为详细的逻辑回归建模，并在变量筛选中采用WOE方式对原始自变量进行了编码。

在初始的外部变量筛选中，共收集172个潜在外部变量及超过1万组样本数据，并以如下方式进行因子筛选：单变量分析（IV值分析）共保留68个因子，相关性分析（Pearson相关性系数）共保留31个指标，WOE转换与指标业务合理性分析共保留20个指标，多重共线性检验共保留18个指标。

在变量筛选过程中，通过WOE转化将数值型变量离散化，并对数值型与字符型变量都赋予WOE编码后取值，不仅在统计学上有效避免了异常值干扰，而且在后续模型维护与实际应用中还具有以下优势：WOE编码有效去除量纲影响，便于进行指标业务合理性分析，同时也便于模型维护中对指标进行PSI稳定性检验。

1.2.3 资产信用风险模型

该模型以PD&LGD为基础，为主要资产类型计算信用风险损失，计算公式为

信用风险损失i=PDi×LGDi×EADi-1×（1-Curei）

式中，i为第i期;PDi为当期违约概率;LGDi为当期违约损失率;EADi-1为上一期违约风险敞口;Curei为违约后在当期转为不违约的概率（如补齐之前的欠款、利息、罚息等）。该模型的影响因子包括资产初始不良率、资产当期增量、资产特征（额度、利率、风险等级）和宏观经济指标等。

在信用风险模型的整体框架方面，主要采用主流的PD&LGD模型。其重要方法为“多类别逻辑回归+迁徙矩阵”的建模形式，通过该模型与宏观经济指标相关联，计算贷款违约概率（PD%）及违约赔付率（LGD%），由此预测某一时间段内的贷款信用风险损失，见图4。

在多类别逻辑回归模型中，如假设一笔贷款的当前PD状态为（PD等级：6），则每个时间周期内（月、季度），PD等级具有以下4种可能的“转移方向”：向好（PD等级：1～5），向坏（PD等级：7～11），违约（PD等级：12），保持不变（PD等级：6）。而这4种“转移方向”的总概率之和为100%。 在此基础上，将每一个“转移方向”与“宏观经济预测”和“贷款数据”做回归，即几率转化为0～1的区间，则

ln Yt 1-Yt =α+β1X1t+β2X2t+…+βnXnt+ε

式中，Y为转移方向概率;X1，2…n为因子（宏观因子、行业因子、区域因子、贷款因子等）;β1，2…n为待估参数;t为时间;ε代表模型预测中的误差值。

在该数字孪生环境构建中，分别对“向好”“向坏”“违约”概率与贷款资产特征和宏观经济指标进行建模，再推算出“保持不变”的概率。获得上述4种概率后，将其代入迁徙矩阵中，推算出贷款的违约概率（PD%）分布见表2。以表2右下角34%为例，其代表根据历史数据测算，等级为11的贷款在下一个模型预测周期转换为等级12（即违约）的概率为34%。

对违约损失率（LGD%）进行预测的计算公式为

LGD=Max  L-R L ，0% =Max  L-V+F-P+T L ，0%

式中，L为清算（核销）时贷款余额;R为抵押物潜在回收率值;V为抵押物回收价值;F为诉讼、佣金等其他费用;P为潜在保险赔偿金额;T为累计的各种税项。在该数字孪生环境构建中，多类别逻辑回归模型会对各参数进行相应的预测，从而计算指定时间窗口内某笔贷款的违约损失率（LGD%）。

1.2.4 资产提前还款模型

该模型用以预测可能发生的提前还款行为，主要影响因子为信用风险模型中的信用风险等级、市场利率变化、贷款剩余年限等。

由于影响提前还贷的因素众多，结合商业银行实际情况，在相关模型构建方面首先设定了借款人风险中性及遵循特定的业务决策规则，即在贷款资产模拟及提前还款模型构建中做如下假设：

（1）模拟中，所有贷款资产的利率皆为可变利率，随整体模拟宏观风险环境变化所造成的利率曲线的变化而变化，若利率上升，则增加借款人的偿还负担。

（2）假设对借款人而言投资收益率总是随机波动，但投资收益率与底层资产和宏观经济指标相关。

（3）假设不存在抵押借款人提前中止合同的违约行为，且假设借款人风险中性，同时借款人在某一时刻决定是否提前偿还贷款时，以净现值方法来评估抵押贷款执行过程中借款人执行策略的损益，若预期收益大于0则提前还款。

（4）假设提前还款行为代表一次性还清剩余贷款余额。

基于此，采集银行5年的提前还款样本，运用比例风险回归模型，即COX回归模型进行建模分析，以提前还款的行为作为因变量，自变量包括市场利率、宏观经济指标等。在参数方面，选用逐步回归方法（向前选择+向后移除的方式），并根据HR值进行变量选取，通过Wald检验和Log Rank检验证明模型的显著性，并通过C-Index指数判断模型的潜在预测效果。

1.3 银行负债端的数字孪生环境构建

对于负债端而言，风险冲击首先会影响市场整体的存款供给情况，再结合银行自身的贷款政策和定价情况，影响每家银行具体的存款增量[3]。存款的存量情况则根据原有合同的到期情况和对存款提前支取情况的预测得到。另外，在负债端，银行可以通过发行债券进行主动负债调节，债券的发行情况取决于银行的策略，其定价则来自银行上一期的不良贷款率，由信用评级所对应的借款利率决定。在银行负债端，主要包含4个模型：市场供应量模型、存款增量模型、债券发行模型和负债（储蓄账户）提前支取模型。

1.3.1 市场供应量模型

该模型同银行资产端的市场供应量模型一致，其主要影响因子也包括宏观经济指标和假设市场原有供应量等。与资产端相似，通过采集区域维度的单位活期存款、个人存款、单位定期存款、其他存款的整体增量数据作为因变量，将宏观、行业、区域等指标作为自变量，并运用多元线性回归建模，共形成4类市场存款供应量模型和112个有效子模型。

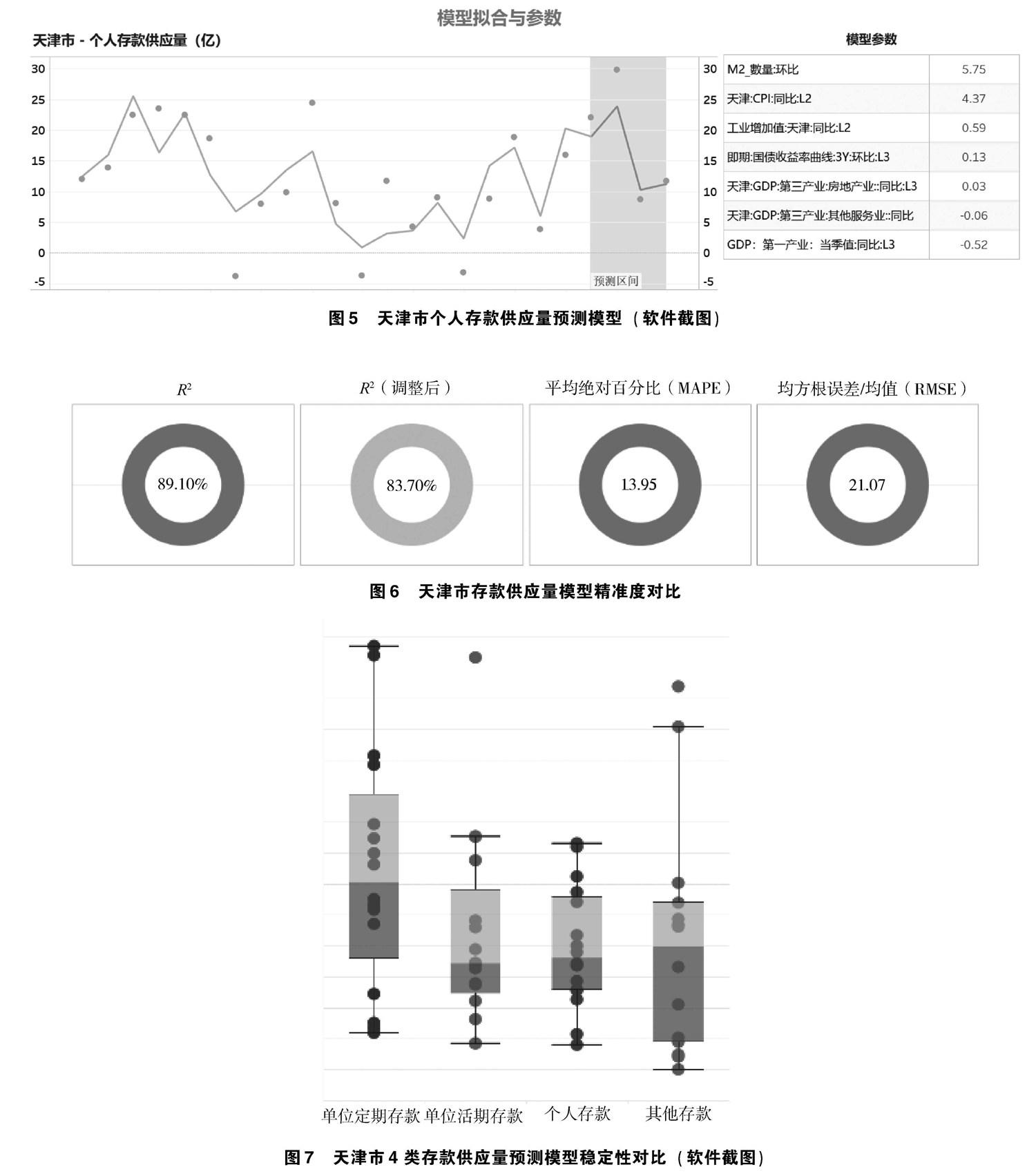
在市场供应量模型中，112个有效子模型以33个区域分布和4个存款因变量类型作为划分维度，以天津市的个人存款供应量模型为例，模拟结果见图5。有底色区域的测试集展现了良好的预测效果，外部因子方面主要包括M2环比、天津CPI、天津工业增加值、天津第三产业GDP等。

在模型精准度测试方面，继续以上述子模型举例，主要通过以下4个指标进行判断，见图6。其中，深色代表其在同类子模型中处于较高水平，而浅色表示中等水平。建模过程中过度拟合及精准度较差的模型被剔除，转而采用单元线性回归方式。

从整体模型精准度看，4类模型中，个人存款的各子模型精准度相对最为稳定，见图7。

1.3.2 存款增量模型

该模型基本与银行资产端的贷款增量模型一致，但负债端暂不考虑资产集中度的相关限制。该模型主要影响因子包括负债价格灵敏度、对手银行定价策略和整体市场供应量模型等。

运用逻辑回归模型对上述4种存款类型在模拟定价环境下的存款增量进行预测，其中，整体市场供应量采用4种存款类型子模型在宏观风险场景下的模型输出。由银行与对手银行定价策略所导致的存款增量变化则建立在虚拟增量客户完全基于市场逻辑而进行决策的考量下，即根据其价格灵敏度模型的输出项及对手银行的定价策略进行计算，模型计算方法如下：

（1）假设在当前模拟环境下有3家对手银行参与模拟，即总银行数量为4家。

（2） 4家银行在本轮模拟中分别就单位定期存款（5年期）给出的定价（由大到小）为3.5%（银行1）、3.25%（银行2）、3%（银行3）、2.75%（银行4）。

（3）某客户手中有1万元的存款供应量，且该客户的虚拟利率敏感性在通过模型计算并进行分位数分布排序后为100%，则在模型逻辑中，出价3.5%的银行获得全部1万元存款。

（4）而若该客户的虚拟利率敏感性在通过模型计算并进行分位数分布排序后为0，则4家银行分别获得2 500元存款。

（5） 而若该客户的虚拟利率敏感性在通过模型计算并进行分位数分布排序后为0～100%（以75%举例），  则出价 3.5%的银行所得存款增量可根据下述公式计算

H=B（1/N）e

H（n，N-1）=（B-∑ 1 n-1  H ×（1/（N-n+1）e）

Hn=B-sum（H1+H2+…+Hn-1）

式中，N为银行总数量;e为利率敏感性区间（0～100%）;H1为出价3.5%的银行所得存款增量;B为存款供应量（1万元），则 H1=3 536（元）、H2=2 834（元）、H3=2 159（元）、 H4=1 472（元）。

1.3.3 债券发行模型

银行发行债券的价格不受银行直接控制，这里假设输入仿真系统的债券发行量必将发行成功，但价格根据评级机构的风险评级决定。而风险评级根据该银行上一个报告周期的贷款不良率对应决定。主要影响因子包含上季度不良率、市场利率和发行量等。

债券的发行定价逻辑主要受到4个维度的影响：债券期限、当期基准无风险利率、信用风险（转换为风险溢价）及隐含期权。

在相关数字孪生环境构建中，针对上述4个维度运用以下逻辑进行设计：发行期限由商业银行自行决定;当前基准无风险利率由模拟宏观经济环境中的利率曲线决定;信用风险将通过资产端信用风险模型对于不同期限的违约率的整体预测，对债券评级进行反向推演，再根据市场上当前对于该评级的风险溢价，推导出公司债券的成本价格;对所发行的债券做了无隐含期权的假设，见图8。

对债券评级推算通过综合历史国内主流评级机构各年的预期违约率数据，综合形成表3中的对应逻辑。

1.3.4 负债（储蓄账户）提前支取模型

该模型用以预测可能发生的提前支取行为，同时加入了不同负债类型历史的客户粘滞度，即利率敏感性信息。

在负债（储蓄账户）提前支取模型的构建过程中，针对以下2个方面进行了深入的数据建模分析探索：一是关于提前支取阈值的探索，二是对储蓄账户中客户利率敏感性的标签画像探索。

在提前支取阈值探索中，结合银行实际情况，首先通过客户滚存行为与客户一次性提前支取行为对客户利率敏感性进行定义——敏感客户：滚存次数=1，且一次性提前支取，支取期限<=T（阈值期限）;不敏感客户：滚存次数≥2或滚存次数=1，且一次性提前支取，但支取期限>T（阈值期限）。

在完成上述定义后，通过数据分析建模的方式对T（阈值期限）的取值进行分析。首先根据不同的储蓄期限种类（3个月～5年）收集大于10万的样本，并对各储种滚存一次且一次性提前支取账户的支取日期与滚存日期之前的时间分布进行曲线绘图和数据分析。通过对一次性提前支取账户数分布曲线的拐点与平稳点分析，获得以下对于模型Y变量标签的方案：

敏感客户。对于定期客户，该账户在观察时点所在月份发生自动滚存且累计滚存次数为1且该账户在滚存后被一次性提前支取，若支取日期距离滚存日期时间间隔小于等于该账户所属储蓄种类下的平稳点所在的支取期限阈值T，则为敏感。

不敏感客户。对于定期客户，若截至观察时点所在月份，该账户累计滚存次数不小于2次，或者当月新发生滚存且累计滚存次数为1，该账户在滚存发生后被一次性提前支取，若支取日期距离最近一次滚存日期时间间隔大于该账户所属储蓄种类下的平稳点所在的支取期限阈值T，则为不敏感。

依据上述逻辑开展的数据建模分析，各期限储蓄种类的支取期限阈值T见表4。

基于此逻辑所采集的Y样本及外部自变量进行了对于客户提前支取利率敏感性的逻辑回归建模，通过从数据清洗、样本转换、变量分析等步骤，最终形成基于以下自变量的利率敏感性模型

P（y=1|X）=-1.88+0.77X1+0.84X2+0.33X3+0.39X4+0.63X5+1.08X6

式中，X1为过去3个月3月期存款和6月期存款占整体定期额度的比例;X2为过去3个月资产管理规模日均余额分层;X3为过去3个月活期资产比重;X4为定期近一个月增长率平滑3期;X5为近3个月定期通过柜面渠道存入笔数比率;X6为过往3个月持有的整体定期存款产品数量。

通过客户利率敏感性模型结果，运用其在历史数据中与提前支取事件进行生存模型建模，从而有效预测在一定时段内，某个存款用户提前支取的概率，并将此概率与存款余额相乘，估算预计提前支取额度。

2 商业银行经营情况评估模型

在不同风险场景和不同定价策略下，根据上述仿真模拟技术应用构建的数字孪生环境能够展现商业银行资产负债表的变化情况，进而可以利用银行核心经营数据计算得出银行的5个核心经营指标，即资本充足率、不良贷款率、净息差、流动性覆盖率及净资产收益率。

资本充足率反映了在存款人与债权人的资产遭遇损失前，商业银行能够以自有资本承担的损失程度，表现了银行抵御风险的能力，公式为

资本 充足率 = 资本-资本扣除项  信用风险 加权资产 +   操作风 险资本 + 市场风 险资本   ×12.5 ×100%

不良贷款率是用以评价商业银行信贷资产安全性的一项重要指标[4]，公式为

不良 贷款率 = 次级类贷款+可疑类贷款+损失类贷款 各项贷款 ×100%

净息差表现了“银行净利息收入”与“银行全部生息资产”的比值[5]，公式为

净息差= 银行全部利息收入-银行全部利息支出 全部生息资产 ×100%

流动性覆盖率表现了“优质流动性资产储备”与“未来30日的资金净流出量”的比值，其标准不应低于100%[6]，公式为

流动性覆盖率= 优质流动性资产储备 未来30日的资金净流出量 ×100%

净资产收益率表现了“净利润”与“平均净资产”的比值，该指标越高则说明投资带来的收益越高，公式为

净资产收益率= 净利润 平均净资产 ×100%

基于上述5个商业银行核心经营指标，结合《商业银行风险监管核心指标》相关要求，进一步加强对商业银行风险进行预测、识别和评估，有效防范金融风险。

3 结语

本文结合商业银行实际，构建了一套在不同系统性风险约束下面向商业银行风险定价决策的数字孪生环境，其中包括风险冲击数字孪生仿真构建、负债端数字孪生仿真构建、资产端数字孪生仿真构建及商业银行经营评估模型。基于上述数字孪生仿真系统可以模拟出不同系统风险下、不同利率定价策略下商业银行的未来经营情况，从而有助于决策者给出面临风险冲击时的合理风险定价决策。下一步工作可以利用深度强化学习技术计算出在系统性风险环境下的最有效风险定价策略，从而使商业银行更好地应对系统性风险。

参考文献

[1] 石言，王彦博，魏文术，等.基于深度强化学习的银行风险定价策略探析[J].中国金融电脑，2020（10）：33-37.

[2] 蒲雨彤，张岭江，范凌杰，等.数字孪生应用与虚拟现实技术发展综述[J].工程技术与发展，2019，1（8）：126-128.

[3]王彦博，张彦超，杨璇，等. 智慧银行视角下的商业银行负债质量管理[J].银行家，2021（6）：18-20.

[4]宋清华，肖心蕙.信贷资产证券化对商业银行盈利能力影响的实证分析[J].统计与决策，2018（24）：172-176.

[5] 丁昆.商业银行盈利能力及风险承担影响因素分析[D].北京：对外经济贸易大学.2018

[6]袁光静.商业银行流动性风险管理研究[D].武汉：武汉大学，2018.