基于动态亚阈值的延迟型PUF 电路设计

张笑天， 汪鹏君,2， 张跃军， 张会红

（ 1. 宁波大学电路与系统研究所，浙江 宁波 315211；2. 温州大学电气与电子工程学院，浙江 温州 325035）

物联网的不断发展助推了便携式设备数量呈现大规模增长的趋势，片上系统(System on Chip,SoC)技术的进步缩短了电子产品开发周期并使之在便携式设备中得到了广泛应用。然而在用户对便携式设备需求增长的同时，信息安全问题也日益凸显。攻击者可通过逆向工程等攻击方式窃取设备中的存储数据[1]，损害了用户与设备厂商的利益。物理不可克隆函数(Physical Unclonable Function, PUF)电路利用集成电路制造工艺偏差产生数字密钥，可有效降低侵入式攻击风险[2]。但随着人工智能技术的不断发展，通过机器学习对PUF 进行模型攻击已成为可能，PUF 面临新型安全问题[3]。此外，由于资源受限型系统中电路面积、电池能量等资源有限，新颖的辅助电路和加密技术无法有效使用，其安全强度受到限制，因此兼具低能耗与高安全性的PUF 电路设计已成为信息安全领域中的关键研究方向[4]。

文献[5]提出了一种低能耗SRAM 型PUF 电路，具有良好的随机性，但随着温度、电压的变化，该PUF 电路的稳定性下降。文献[6]提出了一种亚阈值电流型PUF 电路，具有较低能耗，但其稳定性对温度变化敏感。文献[7]提出了一种亚阈值电流型PUF 电路，能有效抵御机器学习攻击且具有较高稳定性，但是电路面积过大，能耗开销很大。文献[8]提出了一种亚阈值延迟型PUF 电路，利用差分对称设计，提高输出稳定性，虽然通过降低电压减少了能耗，但显著增加了电路延时，并且仍然面临被模型攻击的风险。因此，传统的低功耗PUF 电路已难以进一步提升安全性。

采用亚阈值逻辑是常规低功耗设计方式之一，已有广泛应用。亚阈值特性也可用于提高PUF 电路输出函数复杂度。为进一步提高低能耗PUF 电路安全性，本文提出了一种基于动态亚阈值的延迟型(Dynamic Subthreshold Delayed, DSD)PUF 电路设计方案，并采用TSMC 65nm CMOS 工艺进行验证。该方案将电荷分享效应与动态亚阈值逻辑相结合，能有效降低电路能耗并具有良好的抵御模型攻击特性。

1 仲裁器PUF 电路与动态亚阈值逻辑

1.1 仲裁器PUF

仲裁器PUF(Arbiter PUF, APUF)[9]原理如图1所示。信号传输电路上下对称，C1、C2、···、Cn信号决定E1和E2传播至仲裁器的路径选择情况。因工艺偏差，E1与E2的传播路径延时不相等，它们将在不同时间点到达仲裁器。仲裁器根据这种延迟差输出具有随机性的PUF 响应，其电路输出模型函数如式(1)所示。由于激励会改变信号传输方向，因此w(n)需乘以系数 φ (j)。 φ (j)的计算式如式(2)所示。

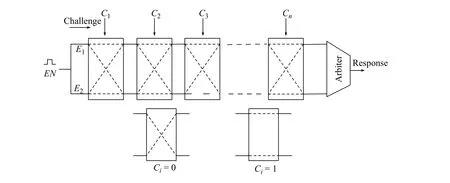
图 1 仲裁器PUF 结构Fig. 1 Architecture of the arbiter PUF

式(1)和式(2)中：r为输出结果；w(n)对应各子路径延迟差；sgn 定义为正值取1、负值取0 的函数；j的取值为1～n；C1～Cn为对应激励信号，其取值均为0 或1。式(1)和式(2)体现了APUF 输出模型函数是一种线性叠加函数，攻击者可对APUF 进行建模并预测输出结果[10]。

1.2 动态亚阈值逻辑

为减少电路功耗，降低电路工作电压是一种常用方式，但降低电压也会带来一系列问题。如图2(a)所示的静态CMOS 与非门(NAND gate)，相同条件下NMOS 漏源电流比PMOS 大，即使输入信号A、B全为低电平，NMOS 亚阈值漏电流也不可忽略。随着电压下降，动态功耗呈平方关系下降，亚阈值漏电功耗却以指数形式增长。当电压下降到一定程度时，静态漏电流功耗成为主要功耗，因此降低功耗就必须抑制其漏电流。考虑如图2(b)所示的动态与非门，当时钟信号CLK为低电平时，电路为预充电状态，通过负载电容CL，Y被充电至高电平。当CLK为高电平时，电路进入求值状态。A和B只要任一个为高电平，Y将被放电至低电平，完成与非逻辑运算。该电路在求值过程并不需要PMOS， 与静态CMOS 相比，相当于可减少两个串联大尺寸PMOS。此外，若输入逻辑数量为N，则静态CMOS 逻辑晶体管数量为2N，而动态逻辑晶体管数量为N+2。在多输入逻辑下，动态逻辑能够节省更多面积，但其缺点是有电荷泄漏以及电荷分享效应。电荷分享效应是指当图2(b)中A、B逻辑仅有一个为高电平时，下拉堆叠网络关闭，但是高电平所控制的晶体管仍具有寄生电容，同样具有储存电荷能力，Y将发生电平偏移。假设VX、VY分别表示X、Y的电压值，初始值分别为0、VDD(电源电压)，VTn为晶体管阈值电压，并以ΔVY表示Y的电压偏移量。此时分两种情况：(1) ΔVY＜VTn，VX终值等于VDD-VTnVX。由电荷守恒定理可得式(3)和式(4)，其中VYfinal代表VY终值，Cα为晶体管N1 的寄生电容值；(2) ΔVY＞VTn，VY与VX处于相同值，可得式(5)。两种情况边界条件可由式(6)确定，当电容之比小于该值，情况(1)成立，否则情况(2)成立。应当控制ΔVY在合理范围，否则电路会发生逻辑错误。

图2 静态与非门和动态与非门Fig. 2 Static and dynamic NAND gate

2 DSD PUF 电路设计

2.1 混合延迟单元电路

混合延迟单元电路采用动态亚阈值逻辑，其结构如图3 所示。电路由晶体管N1～N4、P1～P3 以及反相器I1、I2 构成。时钟信号CLK控制电路预充电、求值状态，当CLK为低电平时，P1、N2、P3 开启，X与Out 被预充电至高电平，而Y被放电至低电平，预充电阶段结束。当CLK跳变至高电平时，电路进入求值状态，由于下拉网络开启，X与Out 将被放电。晶体管P2 漏源电流受X电位影响，随着X电位下降，P2 晶体管漏源电流逐渐增大。因此Y在电路计算过程中处于动态变化状态，称为亚阈值压控结点，N4 晶体管漏源电流也随之变化。由于N4 在时钟刚反转时漏源电流较低，为避免电路噪声影响，需要经缓冲器延时开启，而P3 开启时间与P1 相同，则下拉网络具有较好的稳定性。由于反相器I1、I2 的固有延迟，Y电位上升速度比X放电速度慢，在此期间，N4 栅极电位处于变化状态。电荷分享阵列由5 个并联NMOS 晶体管组成，受激励信号C[4:0]控制，每个晶体管开启都将产生电荷分享效应并引起输出Out 电压偏移。因此，尽管整体下拉网络处于关闭状态(由于缓冲器的延时，晶体管N3 不会立即开启)，每增加一个开启的电荷分享晶体管，Out 都将发生电压偏移。激励信号控制并联晶体管开启数量，并产生不同电压偏移量从而使输出节点电压改变。当CLK经过缓冲器到达N3 晶体管时，Out 开始放电，其初始电压(即下拉网络对应的零输入响应初始值)为改变后的值。因此不同激励信号对应不同的输出函数。

图3 混合延迟单元电路Fig. 3 Hybrid delayed cell circuit

2.2 动态亚阈值判决器

为对混合延迟单元输出进行判决，设计了动态判决器如图4 所示。在电路输入级采用P 型动态反相器设计，晶体管N1、N2、P1、P4 受反相时钟信号控制，A、B信号作为上拉网络输入信号，堆叠NMOS 晶体管有利于平衡PMOS 与NMOS 驱动能力。电路主体为两个对称耦合与非门，初始状态为高电平时，N1、N2 开启，将X1、X2下拉至低电平，因此与非门输出停留在高电平。A、B以不一样的速度降低至低电平时，X1、X2到达对称与非门输入端时间点也不一样，若A下拉速度较快，则M1将被封锁在低电平，此时晶体管N7 被M1封锁，M2通过P6 补充电荷维持在高电平，反之则M1输出高电平，M2输出低电平。为减少负载效应影响，输出级采用一级静态反相器缓冲，并增加N11 与N12 两个休眠晶体管以减少亚阈值静态漏电功耗，仅在CLK为高电平时，输出级下拉网络开启，最终Y1与Y2形成互斥输出，作为判别A、B信号速度快慢的标志。

图4 动态亚阈值判决器Fig. 4 Dynamic subthreshold arbiter

2.3 N 位DSD PUF 电路结构

1 位DSD PUF 单元结构如图5 所示，两个混合延迟单元D1、D2 具有相同激励C[4:0]与时钟CLK输入。D1、D2 的输出信号通过判决器产生1 位PUF 输出信号。在实际应用中，密钥通常具有多位，因此构造8×128 位PUF 单元阵列，从128 位PUF 阵列中分别选出1 位形成8 位并行密钥输出，并扩展激励信号至13 位，构成地址与路径选择信号，其结构框图如图6 所示。最终可在CLK控制下，产生8 位并行数字密钥。

图5 1 位DSD PUF 单元框图Fig. 5 1-bit DSD PUF cell block diagram

图6 N 位DSD PUF 电路框图Fig. 6 N-bit DSD PUF circuit block diagram

3 实例结果与分析

在TSMC 65 nm 工艺下，使用HSPICE 工具进行验证。电源电压为0.4 V 时，电路输出时序图如图7所示(13 位激励信号Cx已省略)。当时钟跳变至高电平，电路开始产生密钥Key，在12 次不同Cx下，每个时钟周期内Key都呈现不同的0、1 分布，具有随机性。通过蒙特卡洛仿真分析并对其平均能耗进行统计，结果如图8 所示，DSD PUF 平均能耗为0.238 pJ/bit，最大能耗为0.305 pJ/bit，具有低能耗特点。

图7 密钥提取时序图Fig. 7 Timing diagram of key extraction

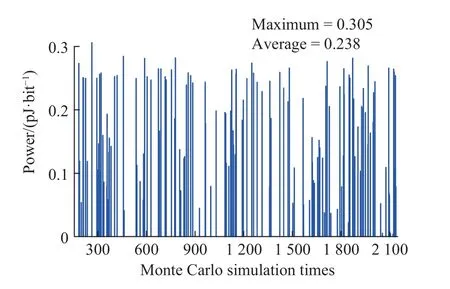
图8 能耗分布Fig. 8 Energy consumption distribution

3.1 DSD PUF 安全性分析

PUF 的随机性以信息熵Entropy 表示，其表达式如式(7)所示：

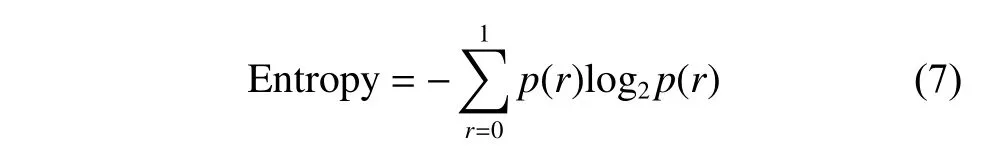
其中，p(r)表示逻辑r的出现概率。对密钥输出进行2 048 次蒙特卡罗仿真分析，仿真结果如图9 所示。高电平输出个数为1 001，低电平输出个数为999。由公式可得信息熵为0.999 999 279。其汉明距离分布如图10 所示，片内、片间汉明距离分别满足μ=0.002 5、σ=0.004 3 与μ=0.497、σ=0.093 的正态分布，其中μ表示数学期望，σ表示方差。

图9 2 000 次蒙特卡洛仿真结果Fig. 9 2 000 times Monte Carlo simulation results

图10 DSD PUF 汉明距离分布Fig. 10 Hamming distance distribution of DSD PUF

在动态亚阈值逻辑下，DSD PUF 延迟时间tdelay_sub满足式(8)所示指数特性：

其中：K为线性系数；CG为负载电容；Vth为晶体管阈值电压；I0为由工艺决定的方块漏极电流；νt为热电压；Won与Lon分别表示充放电过程中等效晶体管的宽与长；n为经验参数。传统模型攻击方式通过搜集一定数量激励响应对(Challenge Response Pair,CRP)代入输出模型公式，计算相关系数并建立对应数学模型从而预测剩余密钥。对于DSD PUF，当激励不同时，下拉网络的零输入响应函数是不一样的。以f(σ1)、f(σ2)分别表示工艺偏差系数σ1、σ2对延时函数指数部分的影响，即使对于具有相同0、1 数量分布的不同激励输入，器件参数偏差也使得指数部分的参数存在差异，该延迟差函数可简化为：

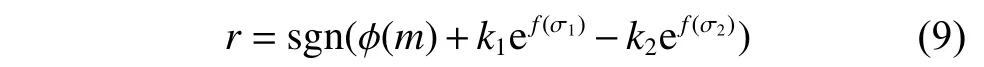
其中：k1、k2为与工艺相关的线性系数； φ (m) 为电路固有延迟。 对DSD PUF 使用人工神经网络(Artificial Neural Network, ANN)算法进行抗攻击验证时，其效果如图11 所示。可以看出，APUF 在训练组数量为500 时，预测错误率便已明显减少。DSD PUF 在训练组数量达5 000 时，预测错误率仍接近理想状态50%。因此DSD PUF 能够有效抵御这类模型攻击。

图11 ANN 算法预测错误率Fig. 11 Prediction error rate by ANN algorithm

3.2 DSD PUF 输出稳定性分析

在亚阈值区，温度对电路性能影响很大，因此对DSD PUF 在不同温度下进行蒙特卡洛仿真验证。晶体管阈值电压与温度负相关，当温度升高时，电路中各晶体管漏源电流明显增加，因此整体速度性能提高。如图12(a)所示，125 °C 工作温度下，电路速度性能提高并且高电平个数为1 000，低电平个数为1 000，随机性接近理想状态。如图12(b)所示，当工作温度降低至-25 °C 时，电路性能明显下降，高电平个数为1 014，低电平个数为986，电路随机性变差。这是由于低温引起亚阈值电流大幅降低，电路延时明显增加并且易受噪声干扰而产生错误。对不同工作电压以及温度下DSD PUF 的误码率(Bit Error Rate, BER)进行统计，结果如图13 所示。尽管高温使得电路具有更高的随机性，但对电路稳定性产生影响。对实验结果分析，DSD PUF 最优工作电压为0.4 V，此时误码率能够达到0.4%，而在最坏情况下误码率为2.19%。与其他相关文献的对比结果如表1所示。可以看出DSD PUF 输出信息熵为0.999 999 279，仅次于文献[13]，具有良好随机性；能耗为0.238 pJ/bit，与同类最优电路相比降低了20.67%。

表1 电路性能比较结果Table 1 Circuit performance comparison results

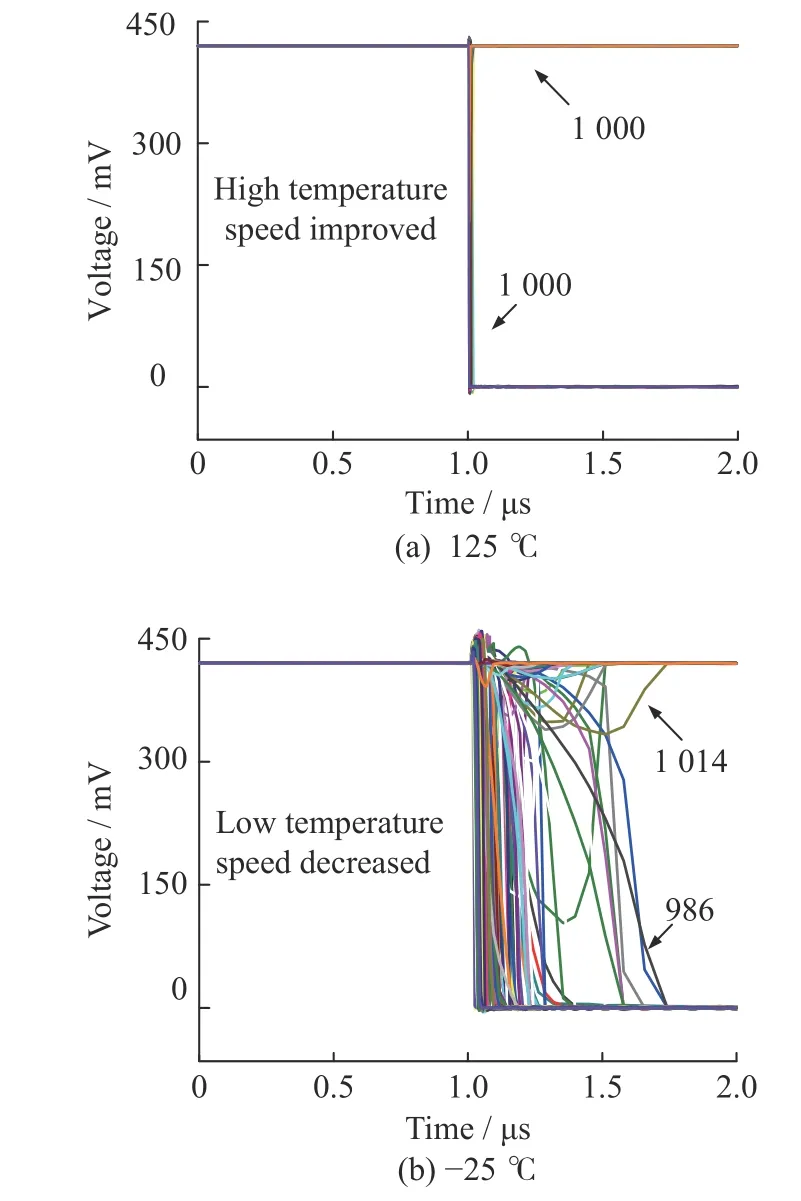
图12 极端温度下的蒙特卡洛仿真情况Fig. 12 Monte Carlo simulation in worst temperature condition

图13 不同温度、电压下的误码率Fig. 13 BER against temperature and voltage variations

4 结 论

本文通过对PUF 电路的研究，结合动态亚阈值特性，提出了一种基于动态亚阈值逻辑的延迟型PUF 电路。该电路主要优点为在动态亚阈值逻辑中，利用电荷分享效应改变不同激励信号下的电路输出函数。采用TSMC 65nm 工艺设计电路并通过HSPICE 验证。结果表明，DSD PUF 电路具有良好唯一性和随机性，其平均能耗为0.238 pJ/bit，与同类最优电路相比降低了20.67%，并能有效抵御模型攻击。