膨胀性土壤中水分反常吸附的分形导数模型1)

田沛博 梁英杰

(河海大学力学与材料学院,南京 211100)

膨胀性土壤是含有较多亲水性矿物成分,具有明显的吸水膨胀和失水收缩特性的塑性土。由于其对环境湿热变化敏感,性质极不稳定。按黏土矿物分类,可以将膨胀土归纳为两大类。一类以蒙脱石为主；另一类以伊利石土和高岭土为主。按膨胀性分类可分为弱膨胀、中膨胀、强膨胀三类[1]。土壤膨胀变形受初始含水量[2]以及自重应力[3]的影响,具有明显的非线性流变特征[4-5],并且膨胀力和膨胀变形随土壤增湿程度增加而增加。在水分渗透吸附的过程中,水分会进入土壤间的孔隙,可侵入黏土的层间,与此同时会逐渐渗透入土体颗粒,引起黏土体积增大的现象。不同污染物在膨胀性土层的扩散过程、含水层在复杂土壤中的渗透过程、垃圾填埋场的选址以及海水倒灌过程均涉及水分在膨胀性土壤中运移规律这一问题。因此研究膨胀性土壤累积吸附过程对工程建设与维护和自然环境保护以及新材料的研发具有重要意义。

吸附性可以解析地定义为土壤含水量和扩散系数的函数。研究表明,水分在均质、各向同性的环境中,其扩散为菲克扩散[6-8],其均方位移为时间的线性函数〈x2〉～t,但在膨胀性土壤中的扩散过程较为复杂,不是菲克扩散,而是反常扩散,其均方位移为时间的非线性函数关系〈x2〉～tα,当阶数α>1 时为快扩散,α <1 时为慢扩散。因此,膨胀性土壤中水分吸附过程偏离正常吸附,为反常吸附过程[9]。近年来,分形导数已成功应用于反常输运相关的物理问题上[10-15],目前的一些主要工作如下。陈文等[16]采用分形Richards 方程推导出更一般的非均质土壤入渗率,并分析了与现有水文模型的关系,其中分形导数的阶数能够刻画土壤的非均质性。曲艺等[17]以Sierpinski 分形地毯构建孔隙分形模型模拟多孔介质空间结构,并根据随机行走模型模拟反常扩散过程。王书鸿等[18]利用时空分形导数模型刻画了软物质的磁共振信号衰减的规律,用以表征和区分软物质的内部结构。Su[19]分析了刚性和膨胀性介质中水分渗流的机制,将分数阶导数引入扩散方程中,在物质坐标下给出了累积吸收、吸收速率和反常吸附率的一般方程。随后Su[20]通过考虑重力项的影响,推导了膨胀性多孔介质中水分运动的分数阶Fokker–Planck 方程,并给出了方程的基本解。Voller[21]通过渗透实验,构建了不同入渗情况下粒子运动的模型,证明了介质的非均质性与反常扩散之间的相关性。张东辉等[22]采用有限容积法构建了粒子在多孔介质中热传导反常扩散模型。基于现有的工作,本文将采用分形导数建立反常吸附模型,准确刻画膨胀性土壤中水分的吸附过程。

需要指出的是,膨胀土受干湿循环过程的影响,土壤颗粒会不同程度地膨胀或收缩。对于膨胀性土壤,使用经典的固定坐标是不合适的。本文考虑引入物质坐标[15]作为描述膨胀性介质吸附过程的媒介。达西定律描述了流体相对于相对不动的黏土颗粒的流动,该物质坐标理论是基于参考黏土质量分布而定义的长度标度,而不是传统的固定长度标度而发展而来的[23]。物质坐标反映固体土壤颗粒的体积与水分的体积之间的关系,通过含水率在垂向的积分体现。物质坐标是含水率和空间位置坐标的函数,通过在垂直方向上积分可以计算出含水率累积吸附量,是描述膨胀土累积吸附的有效工具。因此,本文将基于物质坐标下的分形导数模型,描述膨胀性土壤中水分的累积吸附过程。

1 分形导数累积吸附模型

1.1 物质坐标与分形导数

物质坐标不是基于传统的长度标度,而是基于由吸附剂质量分布定义的长度标度,或者当系统内总质量恒定时,根据两个互扩散组分的质量分布而定义的[23]。考虑到膨胀土壤的特性,采用物质坐标描述其膨胀性。膨胀性介质的物质坐标定义为[24]

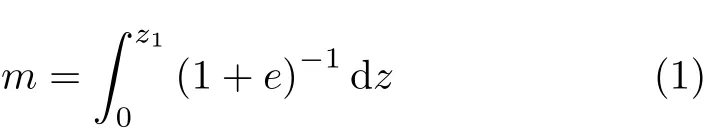
其中z为垂直方向上通常的空间坐标,e为孔隙比,e=ϑ/(1−ϑ),ϑ=ϑl/ϑs为含水率,ϑl和ϑs分别为液体和固体的体积分数[25-26]。

膨胀性土壤中累积吸附的计算表达式[27-28]为

其中t为时间。

时间分形导数的一般表达式[15]为

当t0=0 时,则式(3) 简化为

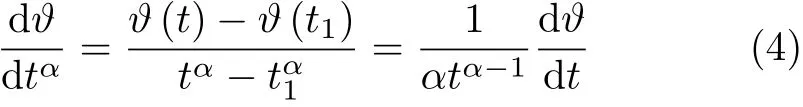
空间上的分形导数为

式(3)～式(5) 中的α和β分别为时间和空间分形导数的阶数,可以描述粒子运动的分形轨迹,描述介质的空间分形维数。构建分形导数扩散方程时[15],通常采用的分形导数为

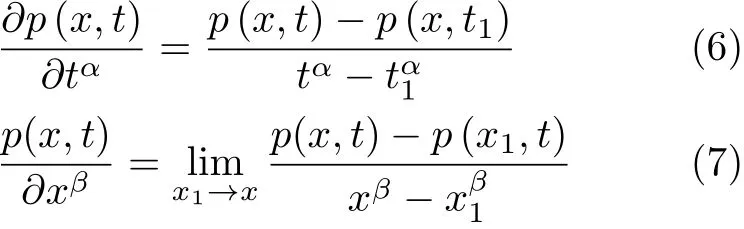
其中p(x,t) 是时刻t下,空间位置x对应的粒子浓度。

在基于非欧距离理论的尺度变换下

分形时空中的扩散方程

其中,Dα,β为扩散系数,是坐标下的拉普拉斯算子,其基本解为

采用式(8),可以得到扩展高斯分布

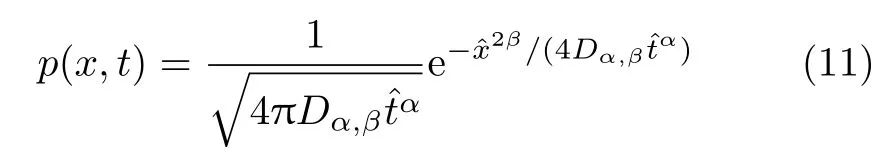
当α=1,β=1 时,式(11) 退化为高斯分布。时空分形导数扩散模型对应粒子的均方位移为[18]

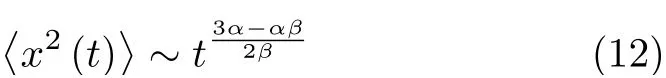
1.2 膨胀性土壤累积吸附的分形导数模型

根据物质坐标,建立膨胀性土壤中水分吸附的时间分形导数扩散波动模型。物质坐标下的分形导数扩散波动方程为

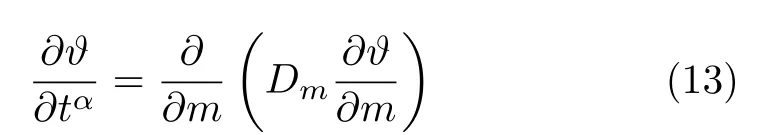
其中α(0< α≤2) 为时间分形导数的阶数。1<α≤2 表征快吸附,0< α <1 为慢吸附,α= 1 时为正常吸附；Dm为扩散系数,cm2/h。初值条件为ϑ=ϑi,t= 0,m >0,边界条件为ϑ=ϑ0f(t),t >0,m=0；ϑ →0,m →∞。其中f(t)为时间依赖的函数,ϑ0为土壤表面含水率,ϑi为初始含水率。

物质坐标下的分形导数扩散波动方程的基本解为

根据式(14),物质坐标m为

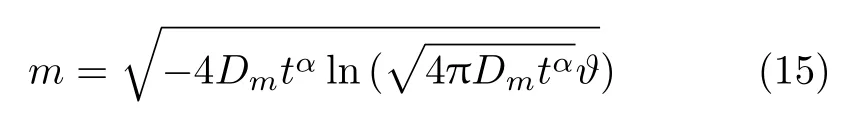
结合式(2) 和式(15),推导分形导数模型对应膨胀性土壤中的累积吸附量

图1 给出了式(16)中不同时间分形导数的阶数(α=0.4,0.6,0.8,1.0),Dm=1 cm2/h,ϑi=0.000 1和ϑ0=0.000 2 对应的累积吸附曲线。由图1 可见,α的值越小,累积吸附量增长得越慢。

图1 分形导数模型的不同阶数α=0.4,0.6,0.8,1.0对应的累积吸附曲线Fig.1 Curves of cumulative adsorption for α=0.4,0.6,0.8,1.0 in the fractal derivative model

需要指出的是,传统模型即整数阶模型,对应膨胀性土壤中水分累积吸附量的表达式为

式中,S为土壤渗吸率,cm/h1/2。

2 分形导数模型应用与验证

2.1 膨胀性黑土中累积吸附过程应用实例

该实验中使用的膨胀性土壤为0.5～1.0 mm 的黑土表层团聚体对应的累积吸附数据[29]。实验中使用了直径为5.09 cm,长为90 cm 的有机玻璃柱,其结构类似于土柱。入渗测量采用与土柱相同的方式进行,随着入渗的进行,张力计元件插入湿润锋后面。当柱底出现毛细管条纹并达到稳态流动时,实验终止。由此,在水流达到稳定之前,可以得到入渗水分随着时间的累积吸附曲线。

分别采用分形导数模型和整数阶模型,即式(16)和式(17)拟合黑土中的水分累积吸附量,其中ϑ0=0.04,ϑi=0.32。运用非线性最小二乘法估计模型的参数,并计算均方根误差,计算公式为

其中I1为拟合结果,I0为实际累积吸附,n为数据个数。

得到分形导数模型的参数α= 0.87,表明水分在黑土中的吸附过程为慢吸附。土壤扩散系数Dm=43.12 cm2/h,模拟结果的均方根误差e0= 0.002 7。整数阶模型的土壤渗吸率S=5.80 cm/h1/2,均方根误差e0=1.264 9。图2 给出了整数阶以及分形导数模型累积吸附I −t的对比曲线。由图2 可知,由于膨胀性土壤在扩散前期具有较强的吸附性,随着吸附量逐渐增加,土壤吸附水分的速率也逐渐放缓,分形导数模型在预测膨胀性土壤中水分累积吸附变化过程上具有明显的优势,均方根误差较小。

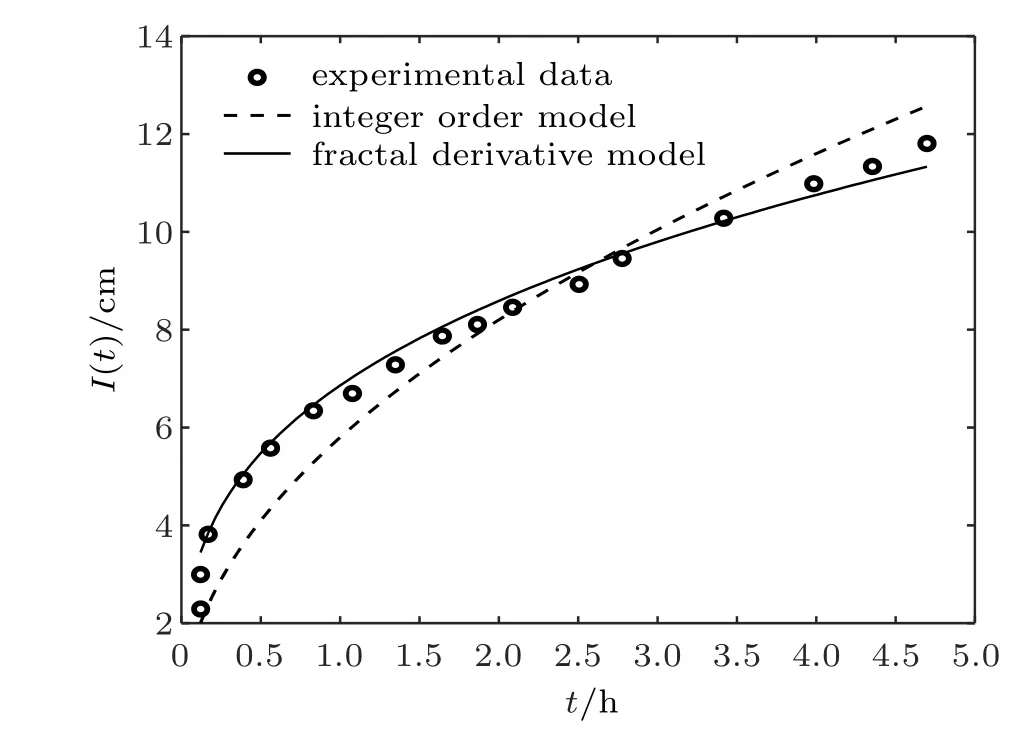
图2 分形导数模型和整数阶模型拟合黑土中水分累积吸附量的曲线图Fig.2 Plots of cumulative adsorption capacity of water in black soil by usingthe fractal derivative modeland integer order model

2.2 砂土中累积吸附的应用实例

对比研究选用膨胀性不明显的砂土累积吸附实验[29]。结合水分在砂土中累积吸附的实验数据,用上述类似的方法处理实验数据,拟合得到分形导数模型累积吸附方程中最合适的匹配参数,参数的值为：α=1.91,Dm=36.37 cm2/h,均方根误差e1=0.004 8。整数阶模型的土壤渗吸率S=6.80 cm/h1/2,均方根误差e0=2.174 7。图3 给出了整数阶以及分形导数模型对应累积吸附量I −t的对比曲线。由图3 可知,对于砂土中的水分吸附过程,分形导数模型在时间分形尺度上与传统的整数阶导数模型相比具有较好的拟合效果。并且时间分形导数模型的阶数大于1 表明水分在此种砂土中的累积吸附为快吸附,膨胀性不明显。

图3 分形导数模型和整数阶模型拟合砂土中水分累积吸附量的曲线图Fig.3 Plots of cumulative adsorption of water in the sand by using the fractal derivative model and integer order model

3 结论

本文基于物质坐标建立了膨胀土中水分吸附的分形导数模型,推导了膨胀性土壤累积吸附与时间的关系,其中时间分形导数模型的阶数能够表征水分在膨胀性土壤中扩散类型,并表征介质的非均质性。通过两个实例,观察到膨胀性土壤具有较明显的吸附特征,其累积吸附对应分形导数阶数的值小于1,表明黑土的吸附过程为慢吸附。砂土累积吸附对应分形导数阶数的值大于1,基本不考虑其吸附力作用。此外膨胀性土壤的累积吸附系数也是反映土壤结构特征的另一个重要指标,需要与分形导数模型的阶数同时考虑,其相关性还需要进一步研究。

通过上述实验,验证了分形导数模型的可行性,并且可以得到分形导数模型在描述膨胀性土壤反常吸附过程较传统整数阶导数模型的优势,分形导数的拟合精度较高,能够较为全面地表征和预测累积吸附的演化规律,并能够对膨胀性土壤的吸附过程进行分类。需要指出的是,对于文献[19] 提出的物质坐标下的分数阶导数模型,采用的是分数阶导数非局部算子,对应的物质坐标是无穷级数的形式。为方便计算,仅采用无穷级数的前两项推导得到了累积吸附的表达式,该累积吸附为时间的幂函数,其中分数阶导数的阶数为1 时,退化为正常吸附。该简化方法降低了分数阶导数模型的精度。而物质坐标下的分形导数模型则不存在此问题。本文的工作为地下土体环境污染的治理和修复提供了新的理论参考。后续将结合不同类型的膨胀性土壤水分以及溶质的吸附实验,验证和推广本文的工作。