铰接车辆模型识别粗糙桥梁频率和振型的数值分析

张文武，亓兴军，肖志全，亓 圣，王珊珊

(1. 山东高速集团有限公司，山东济南 250098； 2. 山东建筑大学交通工程学院，山东济南 250101)

0 引 言

桥梁健康监测在交通基础设施的维护和评估中起着重要的作用。视觉检测是最常用的方法，由于桥梁健康状况的任何变化都会导致其动态特性的变化[1]，因此基于振动试验确定桥梁的模态参数(固有频率、阻尼比、振型)的方法近年来引起了人们广泛的关注。

Yang等[2]在2004年基于车桥耦合理论提出了通过车辆响应识别桥梁模态参数的间接测量法。推导出了理论解析解，并通过数值模拟方法验证了理论的正确性。通过分析检测车垂直方向的响应，即可得出桥梁的频率信息，从而规避了车桥耦合时变系统有载频率变化的限制[3]。随后Lin等[4]在2005年通过现场试验验证了该方法的有效性，说明了间接测量法识别桥梁频率的可行性。Zhang等[5-6]在2012年从移动车辆的动态响应中提取出了振型的平方用来识别损伤。

基于间接测量法识别桥梁频率解析解公式，Yang等[7]在2014年做了进一步的拓展，推导出粗糙桥面下通过间接测量法识别桥梁频率的解析解，并利用希尔伯特变换识别出了简支梁桥的振型，推导出识别桥梁振型的解析解，粗略讨论了桥面粗糙度、车流、车速对桥梁第1阶振型的影响，得到车流基本不会影响振型识别精度，粗糙度对第1阶振型识别影响严重，匀低速行进能够获得更为精准的低阶振型。Malekjafarian等[8-9]对驶过桥梁的双轴车辆振动响应进行研究，将前后2辆拖车对应车轴的响应相减，根据测量车的轴距对桥梁进行分段，利用短时频域分解与重新调节技术从车轴的加速度响应中提取出桥梁的模态振型。Obrien等[10-11]分别在2016、2017年基于间接测量法，将改进的短时频域分解方法应用于实测车辆响应，提取出了高空间分辨率的简支梁桥第1阶振型，用以识别损伤，并利用双轴半车模型进行了数值模拟验证；贾宝玉龙[12]在2016年基于间接测量法从车辆响应中识别出了简支梁桥的前3阶振型，利用第1阶振型进行了损伤识别。Qi等[13]在2017年提出了在冲击激励下通过车辆动力响应识别桥梁振型的方法，在存在白噪声和低等级桥面粗糙度的条件下，利用单轴车在低车速下识别到了连续梁桥的前3阶振型。谢天宇[14]利用间接测量法识别出了简支梁桥的前3阶振型，并进行了变车速、车辆阻尼等相关影响参数的讨论。Kong等[15-17]用2辆沿桥纵向一定距离行驶的车辆提取了振型的平方，用来识别损伤；针对桥面粗糙度对振型识别等不利因素，通过数值模拟研究了利用从大小相同的双检测车过桥时采集的加速度信号进行差值提取桥梁振型的可行性。Yang等[18]发表了桥梁间接测量法的回顾文章，阐明了间接测量法在实际工程应用上的便利性以及研究的不足，特别是在车辆模型上的局限性，指出了实桥试验及实验室模拟存在的困难。贺文宇等[19]基于间接测量法理论，在桥面平整条件下利用识别到的前2阶振型进行损伤识别；阳洋等[20-21]基于间接测量法在桥面粗糙状态下得到桥梁第1阶振型，进而识别了损伤。

关于间接测量法已有大量的研究，由于其较大的便利性和经济性，该方法的发展前景广阔。然而研究的桥梁形式多为简支梁桥，对于振型识别一般局限在低车速、较低阶振型范围，车辆模型多为单轴车辆模型且多是平整桥面下的研究。

针对以上研究的不足，本文基于间接测量法，选用实际工程中某3跨连续梁桥进行数值模拟分析；通过使用汉宁窗抑制高频信号的泄露，突破低车速识别的限制条件；改进车辆建模方式，利用2辆单轴1/4车辆模型模拟测试车辆，1辆双轴半车模型模拟牵引车辆并对桥梁提供额外激励，三车铰接以便于实际应用；对前后车测试出的加速度数据进行相减处理以消除桥面粗糙度的影响。本研究可进一步完善间接测量法识别桥梁频率和振型的相关理论，推动间接测量法识别频率和振型在实际工程中的应用。

1 理论基础

桥面不平整度是一种零均值、各态经历的平稳高斯随机过程，通常使用功率谱来描述。参照《机械振动 道路路面谱测量数据报告》，公路路面功率谱密度拟合函数为

(1)

式中：m0为参考空间频率；m为空间频率；Gx(m0)为参考空间频率m0下的路面功率谱密度值，称为路面不平整度系数，它取决于路面等级；ω为频率指数，取值为2。

每一类粗糙度的振幅d为

(2)

式中：Δm为空间频率的采样间隔。

路面粗糙度叠加r(x)为

(3)

式中：ms,i为第i个空间频率；di和θi分别为第i个余弦函数的振幅和相位角。

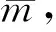
图1 单自由度车辆通过桥梁简图Fig.1 Schematic Diagram of Single-degree-of-freedom Vehicle Passing Through a Bridge

采用有限元方法将桥梁离散化，车辆振动方程可以表示为

(4)

桥梁的运动方程可列为

(5)

式中：qv(t)为车体的竖向位移，值得注意的是对于车体的竖向位移，本文是从车体平衡位置起算的，抵消了车体重力的作用；δ为单位脉冲函数。

接触力fc(t)为

fc(t)=-mvg+kv[qv(t)-ub(x,t)|x=vt]-

kv[r(x)|x=vt]

(6)

式中：g为重力加速度。

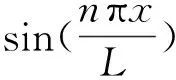
(7)

(8)

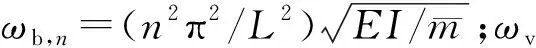
由于粗糙度引起的车辆悬架弹性力和车辆惯性力对桥梁响应贡献较小，因此式(8)简化为

(9)

对于零初始条件，求解式(6)得

(10)

式中：Δst,n为车辆质量引起的桥梁静态挠度，Δst,n=-2mvgL3/(n4π4EI)；Sn为量纲一的速度参量，Sn=nπv/(Lωb,n)。

将式(10)代入式(7)，得到桥梁的竖向位移为

Snsin(ωb,nt)]}

(11)

对于车辆，式(7)的运动方程可以改写为

(12)

将式(11)和式(3)代入式(12)，通过带哈密积分得到车辆竖向位移为

(13)

对式(13)进行2次微分得到车辆的加速度响应为

ns,ivωvsin(θi)sin(wvt)]

(14)

粗糙度引起的车辆加速度响应为式(11)的后半部分。车辆的加速度响应主要由4种不同类型的频率余弦波叠加组成，分别为车辆的固有频率ωv、驱车频率(n±1)πv/L、桥梁的左移频率ωb,n-nπv/L和右移频率ωb,n+nπv/L。通过恰当的滤波技术(比如快速傅里叶变换FFT、希尔伯特转换HT等)，桥梁的n阶频率所对应的信号信息可以从车辆的振动加速度响应中提取出来。

为了提取出桥梁振型，采用带通滤波数据处理手段从车辆的振动响应中提取出与第n阶振型桥频对应的分量响应。根据式(14)得到与第n阶模态相关联的桥频分量响应Rb为

(15)

对式(15)整理得桥梁振动响应的瞬时振幅解析解A(t)为

(16)

通过式(16)可以看出，A(t)为一个常量Am与桥梁模态函数sin(nπx/L)绝对值的乘积，所以A(t)仍是桥梁的模态函数。以此可以得出，只要从车辆竖向振动响应中分解出对应于桥梁某阶频率的振动响应，那么就得到了相应的瞬时振幅振荡曲线，曲线的外包络线则代表了桥梁相对应的某阶振型。由于测试车通过了桥上的每一个点，因此可以保证此方法提取振型具有较高的空间分辨率。

2 识别流程与模型参数

2.1 识别流程

通过试验车辆的动力响应识别相应的桥梁频率和振型步骤如下：

步骤1：通过在测试车上放置加速度传感器测得车辆的竖向加速度振动响应。

步骤2：对提取出的车辆加速度时程响应进行快速傅里叶变换识别出桥梁频率。

步骤3：通过带通滤波器与汉宁窗将不同桥频的响应从车辆振动响应中分离得到相应的桥频分量响应。

步骤4：运用希尔伯特变换获取相应桥频分量瞬时振幅曲线，应用此曲线重构桥梁振型，瞬时振幅曲线在绝对值上代表了桥的相应振型，振型的正负需要根据工程实际进行判断。

2.2 模型参数

基于分离法原理与车辆动力学理论,将车辆模型与桥梁模型分别建模，利用约束方程实现任意时刻车轮和桥面接触点的位移协调关系，车辆与桥梁2个独立子体系之间的耦合关联作用是通过轮桥接触点的相互作用力相联系(相应的力平衡关系自动满足)，通过APDL编程实现车辆过桥的耦合动力时程响应分析。本文选取实际工程中某3跨连续梁桥进行数值模拟分析。

2.2.1 桥梁建模

工程实例为济南市政某28 m+45 m+28 m连续梁桥，桥面宽度为8 m，上部结构为单箱单室主梁。全桥主梁采用C50预应力混凝土，弹性模量EC=3.45×104MPa。因为是用单梁模拟主梁，横向刚度扩大1 000倍，滤除扭转对桥梁模态识别的影响。桥梁横截面如图2所示。桥梁纵梁相关参数如表1所示。

表1 桥梁纵梁参数Table 1 Parameters of Bridge Longeron

图2 桥梁横截面(单位：cm)Fig.2 Cross Section of Bridge (Unit:cm)

应用以上相关桥梁参数，使用有限元软件建立桥梁模型，运用模态分析模块得到自振频率和振型，如表2所示。

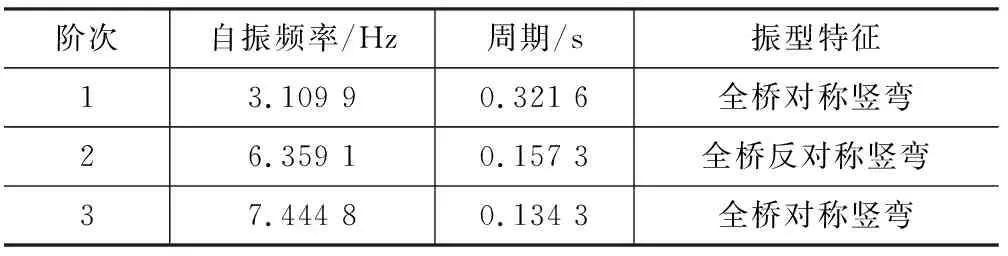
表2 桥梁自振频率与振型特征Table 2 Natural Vibration Frequency and Mode Characteristics of Bridge

2.2.2 车辆建模

车辆模型采用铰接车辆模型，让其匀速驶过桥梁，车辆实际模型及车辆有限元建模如图3所示。

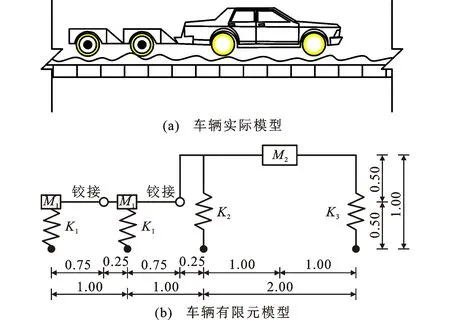
图3 铰接车辆模型示意图(单位:m)Fig.3 Schematic Diagram of Articulated Vehicle Model (Unit:m)

2辆单轴测试车质量M1各为1 t；双轴牵引车质量M2为30 t；牵引车点头刚度Iv为1×104kg·m2；单轴车竖向刚度K1为1.7×105kN·m-1;双轴车前轴竖向刚度K3为1.11×106kN·m-1；后轴竖向刚度K2为7.4×105kN·m-1。

牵引车通过双轴半车模型模拟，测试车通过单轴1/4车辆模型模拟，车体之间通过铰连接。相比于单轴1/4车辆模型，双轴半车又添加了车体质量点的转动刚度，因此多了一个转动频率。通过理论公式计算得到车桥模型中的单轴1/4车和双轴半车竖向振动频率ωv分别为1.22、2.08 Hz，双轴半车转动频率ωθ为2.17 Hz。双轴半车竖向振动频率和转动频率计算公式如式17所示。

(17)

3 不同不平整度等级下频率和振型的识别

桥面不平整度是桥梁间接识别方法在实际应用中无法避免的一个重要影响因素。Chang等[22]提出了使用2个单自由度车辆模型匀速通过粗糙桥面，然后对得到的2条加速度时程曲线分别进行快速傅里叶变换，将得到的2个频谱图进行相减，以达到消除桥面不平整度对间接测量法的影响。Elhattab等[23]提出采用2个单自由度车辆模型匀速通过粗糙的桥面，得到前后2辆车在过桥阶段的加速度时程曲线，然后选取它们在桥面同一位置时的加速度数值相减，使用加速度差值曲线进行模态分析，进而消除桥面不平整度对识别结果的影响。本文采用后者原理进行模拟分析。

参照《机械振动 道路路面谱测量数据报告》，路面(桥面)按照功率谱密度可以分为8级，前3个等级如表3所示。

表3 路面等级Table 3 Road Level

采用简谐波叠加法(三角级数法)，在车速10 m·s-1时，使用MATLAB程序生成101 m长路面(桥面)A、B、C级的不平整度系数，进而进行计算。C级不平整度MATLAB核心代码示例为

qkc(i,:)=Xkc(i)*sin(0.1*pi*fk(i)*

dL+faik(i))

101 m长桥面不平整度模拟如图4所示。

图4 桥面不平整度模拟Fig.4 Bridge Deck Roughness Simulation

3.1 频率识别

对桥面分别施加A、B、C级不平整度，通过前后测试车加速度做差得到差值加速度，对差值加速度进行快速傅里叶变换，其频谱图如图5所示。

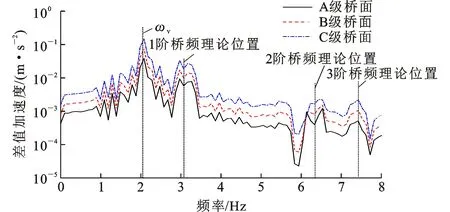
图5 铰接车辆识别频谱Fig.5 Articulated Vehicle Identification Spectrum

根据式(14)，其解析解中包含与粗糙度相关的频率、驱车频率、测试车自振频率、桥梁左移和右移频率，可以认为桥梁左移和右移频率的均值为桥频。对前后测试车加速度数据进行差值处理能够有效消除粗糙度相关频率信息，显著降低驱车频率振动峰值，因此从频谱图只能看出测试车自振频率及桥梁前3阶频率信息。随着不平整度等级的增加，2阶、3阶等较高阶桥频分辨率略有下降，但仍能够清晰辨别，说明采用铰接车辆模型进行差值处理能够较好克服粗糙度的影响。

表4为不同桥面不平整度等级下频率识别值，由表4可知，桥梁频率识别相对误差都能控制在1%以内，满足工程精度要求。

表4 不同桥面不平整度等级下频率识别值Table 4 Identification Frequency Values of Different Bridge Deck Roughness Levels

3.2 振型识别

通过带通滤波器与汉宁窗数据处理技术将不同桥频的响应从车辆振动响应中分离得到相应的桥频分量响应。A级不平整度下桥频分量响应如图6所示；B级不平整度下桥频分量响应如图7所示；C级不平整度下桥频分量响应如图8所示；对桥频分量响应的外包络线重构得到桥梁的识别振型。

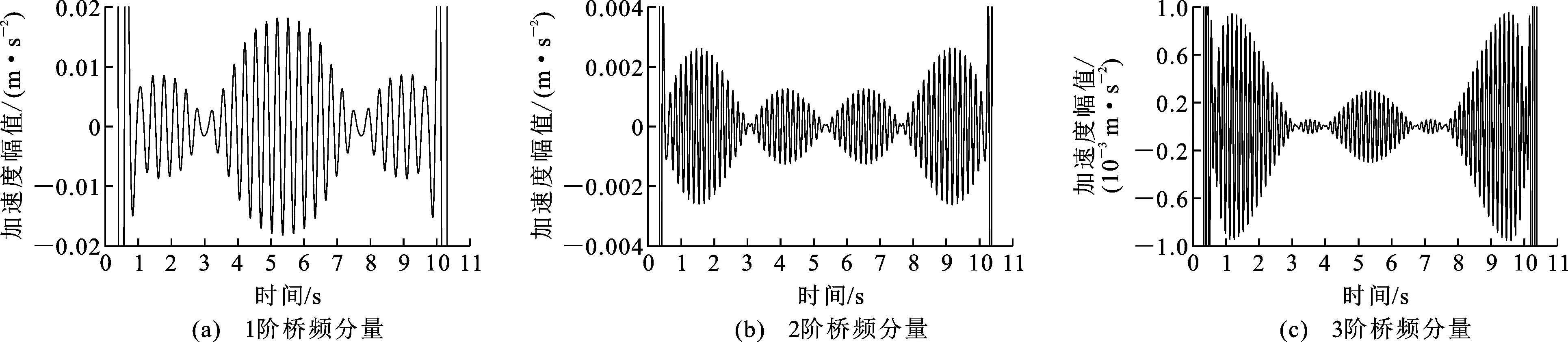
图6 A级不平整度下桥频分量响应Fig.6 Bridge Frequency Component Response Under Class A Roughness

图7 B级不平整度下桥频分量响应Fig.7 Bridge Frequency Component Response Under Class B Roughness

图8 C级不平整度下桥频分量响应Fig.8 Bridge Frequency Component Response Under Class C Roughness

桥频分量响应边界处有少量异常点是因为使用汉宁窗后旁瓣衰减所致，可以在数据处理时人为去除。另外边跨外包络线误差较大，这是由车辆上桥下桥时在两铰接小车长度范围内无有效的加速度差值数据导致，后期振型处理时应当做适当的数据修正。将识别振型与有限元模态分析得到的理论振型最大值归一化处理后进行对比分析，讨论其识别精度。桥梁前3阶振型如图9所示，其中相对位移为桥梁单元之间的相对位移。

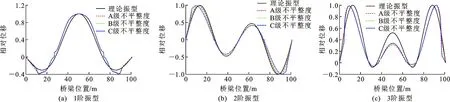
图9 桥梁振型Fig.9 Bridge Vibration Mode

利用此数值模拟方法得出的识别振型与桥梁有限元模型模态分析得出的理论振型进行对比，分析此数值模拟方法的准确性，衡量标准采用振型模态保证准则，模态保证准则(MAC)定义为

(18)

式中：M为MAC值；φa和φb分别为提取的模拟振型向量和理论振型向量。

粗糙度对振型识别影响较大，由于粗糙度与桥梁一起充当了激励源，因此车辆振动信息中包含了粗糙度与桥梁振动的信息，加速度差值可以减弱粗糙度的干扰但并不能完全去除其影响。当桥面粗糙度较大，而车辆对桥梁的激励不足时，粗糙度信号会掩盖桥梁信号导致桥梁振型难以识别。本节探讨了不同等级不平整度对桥梁振型识别的影响，采用质量较大的牵引车增加对桥梁的激励，通过前后测试车响应数据差值消除桥面粗糙度的不利影响，总体上取得了较好的桥梁振型识别效果。

振型曲线有突变是因为振型曲线的正负根据工程实际处理所致。从图9可以看出：振型识别误差主要来源于2个边跨区段，随着桥梁振型阶次的升高，边界异常效应愈加明显；第3阶振型的桥梁中跨跨中位置识别误差较大，其根本原因来源于2阶桥频信号的污染以及振型最大值归一化时边跨区段的影响。表5为不同桥面不平整度等级下振型识别MAC值，通过表5可以看出：桥梁振型前2阶MAC值基本都在0.97以上；1阶MAC值较2阶MAC值低，原因为桥梁振型1阶模态信息受车辆高能量信号的污染；3阶MAC值在0.94以上，能够满足工程精度要求。

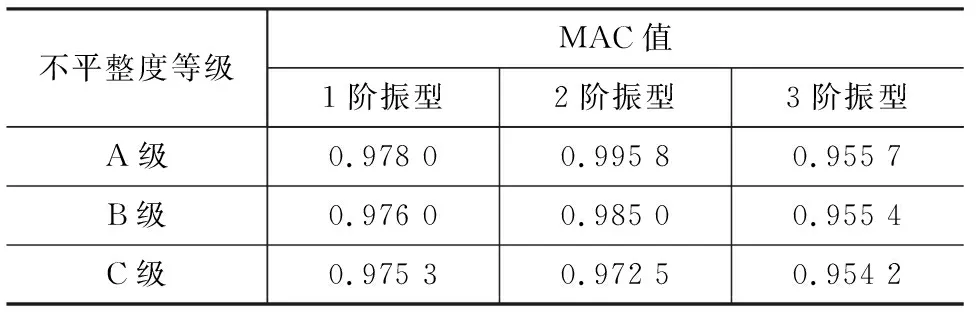
表5 不同桥面不平整度等级下振型识别MAC值Table 5 MAC Value of Vibration Mode Recognition Under Different Bridge Surface Roughness Levels

4 结语

(1)本文对车桥耦合振动计算得到的车辆响应采用带通滤波与汉宁窗相结合的处理方法，解决了间接测量法识别振型必须保持低速条件的限制，使得较高车速下能够较为准确识别到桥梁第3阶振型。

(2)桥面不平整度是车辆响应中重要的不利激励源，本文采用铰接车辆模型，利用质量较大的牵引车作为社会车辆对桥梁施加额外激励，通过对被拖引的前后测量车响应数据进行差值处理，克服了桥面粗糙对桥梁频率振型识别的不利影响，数值分析结果显示在A、B、C级桥面不平整度条件下，采用铰接车辆模型识别出的桥梁前3阶频率相对误差均在1%以内，对加速度时程响应数据加窗处理后识别出的桥梁前3阶振型MAC值均在0.95以上，满足工程精度需求。

(3)利用此铰接车辆模型的振动响应识别桥梁振型不需要在桥上设置传感器，只需要在铰接的测试车辆上各安装1个传感器即可测量识别得到桥梁频率和桥梁的连续分布振型，其振型曲线相当于在桥梁上直接安装无限个传感器得到的实测振型，因此具有经济且快速的优势，应用前景广阔，但是相关研究工作仍然不够完善，比如忽略了桥梁阻尼和车辆阻尼的影响，另外现场测量白噪声也是不可忽略的因素，因此对于在工程上的应用还需要进一步的理论和现场试验研究。