桶形基础稳定性与地基极限承载特性分析*

张 旭

(1.中葡新能源技术中心(上海)有限公司，上海 200335；2.上海勘测设计研究院有限公司，上海 200335)

0 引言

近年来我国海上风电进入快速发展期，我国沿海距岸边50km范围内可开发的海上风能资源为7.58亿kW，大约是陆上实际可开发风能资源储量的3倍。随着海上风电的大力发展，对风电基础的要求越来越高，目前常用基础形式有重力式、桩基础、导管架、浮式基础和吸力桶基础等形式，其中桩基础相对最为常见，海上风电桩基础和支撑结构占比约30%[1]。

吸力桶基础作为单桩基础的替代形式，是海上风电新型基础，能有效降低基础成本约30%[2]。吸力桶基础多为底端开口、顶端封闭的大直径圆桶，具有成本低、施工工艺简单、一体化施工、二次使用等优点，可实现快速安装，能较好地适用于我国沿海区域的海洋地基[3]。同时，吸力桶基础能较好地抵抗风电机组承受的较大水平荷载和弯矩，在最近几年得到较好发展。一些学者开展了桶形基础受力与承载的相关研究，如Barari等[4]与Sun等[5]基于莫尔-库仑弹塑性模型，分析了桶径与贯入比对桶体极限承载力的影响。刘振纹等[6]通过有限元计算，分析了桶形基础的竖向破坏模式，基础埋深范围内的土体强度，以及基础形状对地基竖向承载力的影响。刘梅梅等[7]通过有限元计算，得到竖向加载作用下不同长径比的桶形基础承载特性与失效形式，提出在计算极限承载力时，可考虑将桶与桶内土体作为一个整体进行简化分析。朱斌等[8]与Achmus等[9]通过模型试验和数值模拟方法研究了吸力桶基础的水平承载力。Zhang等[10]通过离心模型试验研究，指出桶形基础在长期荷载作用下会发生较大沉降和侧向位移。Hung等[11]借助有限元探讨了在不同不排水抗剪强度下，桶形基础的承载力随长径比的变化，并分析了桶体在水平和竖向荷载作用下的运动形式及基础周围土体的破坏机理。Wu等[12]在饱和软黏土中对桶基础进行分析，得到竖向荷载作用下的极限承载力，提出软黏土的不排水抗剪强度、土体各向异性及吸力桶基础的长径比都是影响吸力桶基础竖向承载力的主要因素。Bagheri等[13]分析了单调和循环荷载作用下桶形基础的变形行为，指出在桶盖附近会发生较大水平位移。

因此，海上风电长期服役进程中，在风暴潮等多模式、多工况荷载作用下，研究吸力桶及地基基础的极限承载性能具有重要工程意义。

1 本构模型与参数计算

土体本构模型为各向同性弹塑性模型，采用Mohr-Coulomb(M-C)准则，其力学模型为：

(1)

式中：σ1，σ3分别为最大、最小主应力；f为屈服函数，且f>0时，材料处于塑性流动状态，f<0时，材料处于弹性变形阶段，f=0时，材料处于弹塑性临界状态。

以上即为剪切破坏判据，拉伸破坏判据为：

ft=σt-σ3=0

(2)

式中：σt为岩体抗拉强度。

岩土的体积模量、剪切模量分别由下式计算：

(3)

(4)

式中：K，G分别为体积模量、剪切模量；E为弹性模量；ν为泊松比。

对于接触面参数，法向刚度kn，剪切刚度ks，取接触面相邻区域“最硬”土层等效刚度的10倍[5]，即

(5)

式中：Δzmin为接触面法向连接区域上最小尺寸。

根据现场地质勘察报告，结合室内试验，综合确定的地层力学参数如表1所示。由式(3)～式(5)计算的接触参数如表2所示。

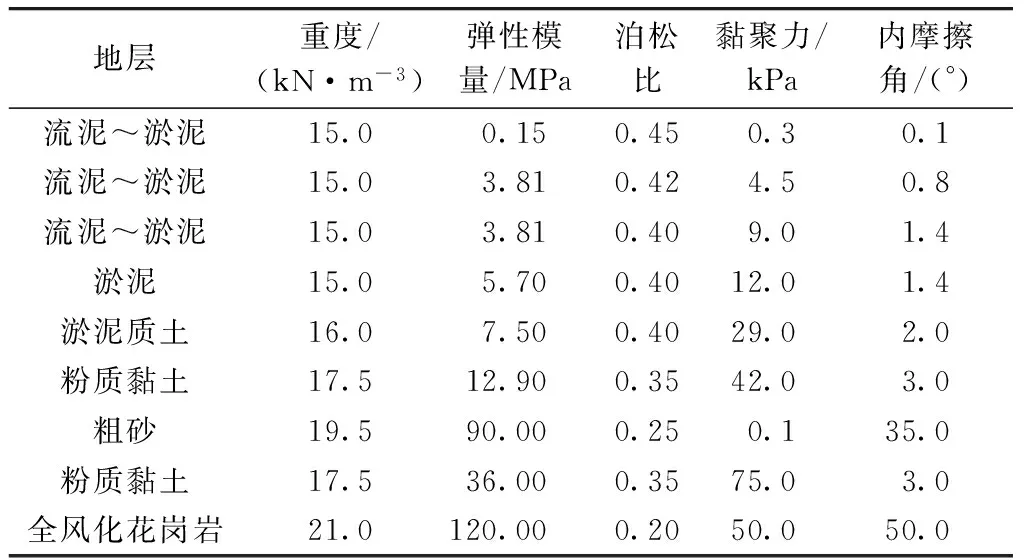
表1 物理力学参数

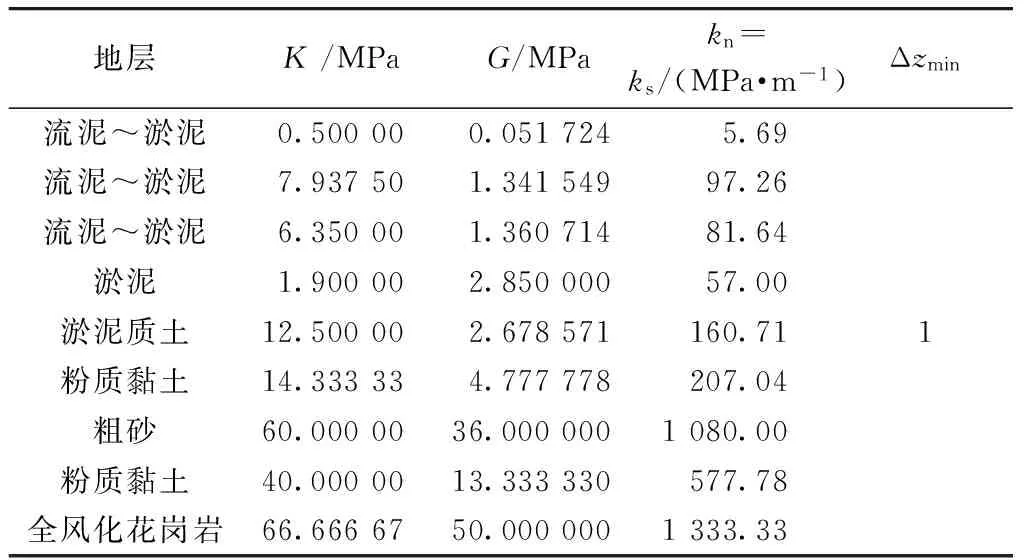
表2 接触参数

考虑吸力桶主要所受荷载，即上部风机重力、风机所受风荷载传递下来的水平力、弯矩、扭矩，以及水中等效波浪力的联合作用，风机荷载包括自重 9 056kN、水平力2 584.7kN、弯矩258 179kN·m、扭矩12 980kN·m，波浪荷载为18 526.83kN。其中，水平荷载即风机所受的风荷载传递下来的水平荷载；波浪荷载为水中塔筒所受的波浪力，通过水下塔筒表面上水的高度(作用水柱高度14.12m)计算出来的等效波浪荷载。联合荷载作用如图1所示。

图1 吸力桶受荷示意

由于单柱复合桶高度较高，且各部分构件结构特征不同，加工工艺不一，在陆上建造时，将基础分为上部桶体结构(基础顶法兰以下17m立柱)、中部过渡段及下部钢桶进行分别预制，然后进行组装合龙。单柱复合桶形基础安装施工，包括陆上建造及总拼合龙、运输及海上安装，总体工艺流程为陆上分段预制→基础合龙→绑扎出运→基础海上安装→基础防冲刷施工。

2 三维模型构建

根据广东地区某海上风电场工程地质条件，联合Rhino三维建模与有限元软件，建立吸力桶-地层的大尺度场三维数值模型，并通过编写结点、单元、坐标系统的Fish语言转换程序，导入有限差分岩土软件，如图2所示，吸力桶外桶直径36m、壁厚25mm，内桶直径10m、壁厚15mm，内设6块分舱板，泥面以上塔筒高45m，桶嵌入地层约13m。建立的地层模型长度为外桶径的10倍即360m，高54m。单桩复合桶的单柱部分分上、中、下3段，其中上段直径7m、壁厚70mm、高20m，下段直径10m、壁厚75mm、高11m，中段为连接上、下段的过渡段，壁厚70mm、高14m。泥面桶盖厚30mm。

图2 吸力桶-地层三维模型

地层上边界为自由无约束边界，底部采用固定位移约束，地层侧面采用x，y约束，吸力桶无固定约束，仅施加联合荷载。z向应力场将在计算中由自重自动计算产生。

将有限元模型划分网格，吸力桶-地层整体模型共划分90 252个单元、101 812个结点。吸力桶及靠近桶的土层采用加密处理，距吸力桶较远部位网格逐渐稀疏。其中，吸力桶(含肋板连接件、分舱板、圆板)的网格剖面如图3所示。

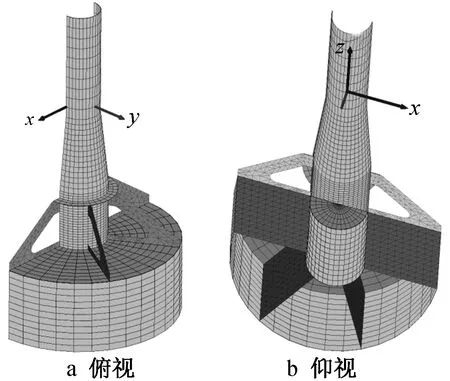
图3 吸力桶结构剖面

为了模拟吸力桶、土间的真实接触、滑移、分离状况，在吸力桶、地层间设置接触面：桶盖板-土接触、桶侧壁-地层接触、桶底端面-土接触，如图4所示。

图4 吸力桶、地层间接触面

3 变形分析

隐藏吸力桶的肋板、分舱板，为便于更好地观察桶身与土层变形，分析吸力桶、土间变形及其相互作用。

吸力桶-土整体的水平向(x)位移矢量云图如图5a所示，总体上可看出，位移基本都集中在桶上，最大水平位移为252mm，出现在桶上部，最小水平位移为0.276mm。土体变形主要集中在桶附近的较小区域，且基本出现在浅层，约为嵌入土中的桶高一半，在桶高一半位置以下的土层，其水平变形极小。

图5 吸力桶-土的水平向与竖向位移矢量云图(单位：m)

吸力桶-土整体的竖向(z)位移矢量云图如图5b所示，可看出右侧与桶相邻的小区域受桶的偏转作用，出现挤压隆起变形，“上翘”30.5mm；由于桶向右偏转而与土脱开，左侧土层临空，出现一定程度的“倾倒”下沉。

吸力桶、土间的接触状态如图6所示，通过剪切滑移接触可看出，桶侧壁与土层接触良好，桶盖与土层间基本无剪切滑移行为，桶盖与土为法向受压接触。

图6 接触面的接触状态

根据位移计算结果计算泥面转角，[(105.8mm+28.6mm)/(36 000mm)]×100%=0.373%<0.436%，满足安全要求。

4 受力与屈服分析

吸力桶身最大主应力云图如图7所示，由于桶身在组合外荷载工况下向右偏转，桶身所受最大拉应力出现在内桶与桶盖交界处的内桶壁，约30MPa。

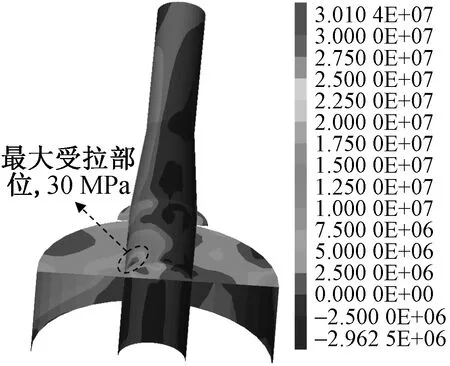
图7 桶身最大主应力云图(单位：Pa)

桶身最小主应力云图如图8所示，桶身最大受压部位为内桶的底端中间部位，约78MPa，比桶身所受的最大拉应力30MPa大很多。桶盖以上的桶身左侧部分基本处于受拉状态，为主要的受拉区，应力值为正。

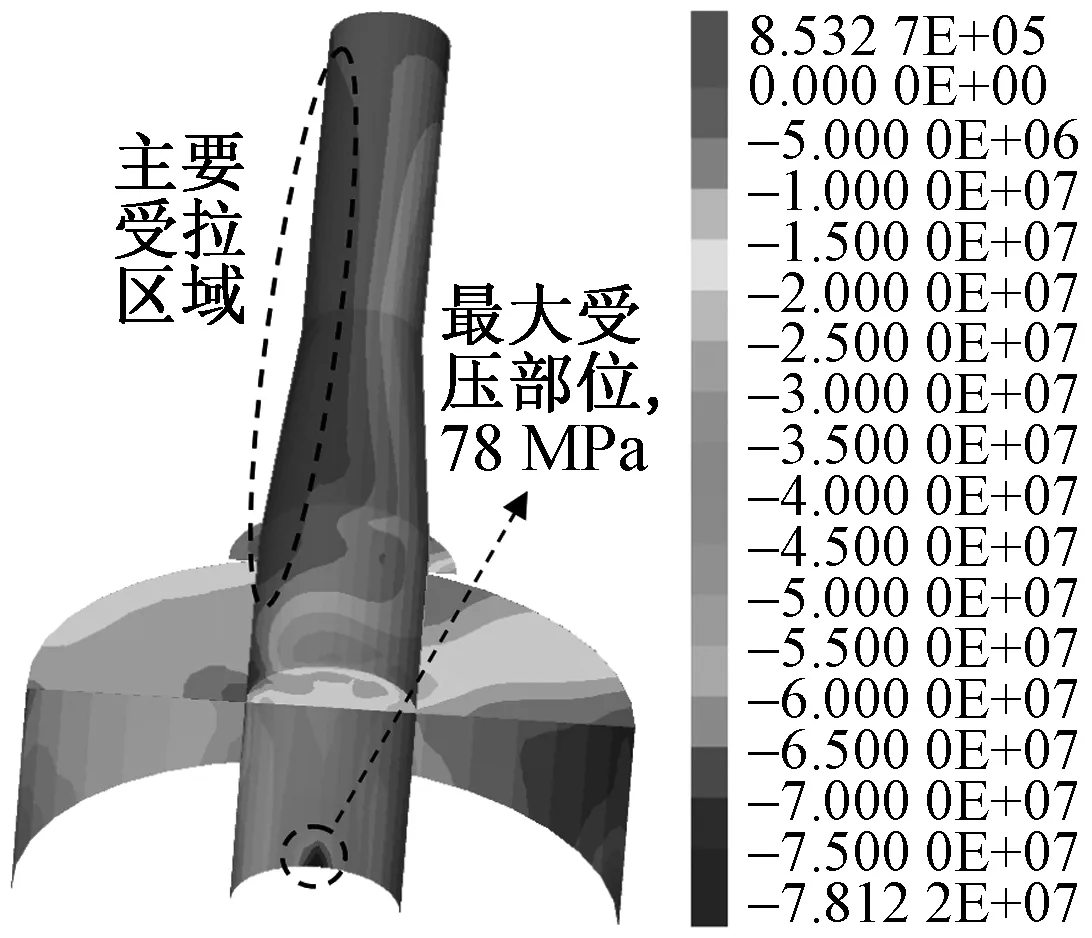
图8 桶身最小主应力云图(单位：Pa)

由于桶体在外荷载作用下向右偏转，桶体右侧受压，外桶上部的桶单元体应力演化曲线如图9所示，在多工况荷载作用下，该部位单元体与土体相互作用，受挤压，压应力逐渐增大，外桶体所受压应力>1MPa后基本趋于稳定，表明其附近的土体与桶体处于应力平衡状态。

图9 单元体(外桶上部)的应力演化特征

土体屈服区如图10所示，可明显看出，内、外桶的相邻土层破坏，且以外桶的外圈土破坏为主，其中受压侧(右侧)土体破坏程度明显高于非受压侧(左侧)。左侧上表层为浅层破坏，右侧为受压侧，土层破坏深度深于左侧。

图10 土层最大剪应变增量云图

无论内桶还是外桶，其桶外壁土的破坏程度高于桶内壁土，外桶的外圈土破坏程度高于内桶的外圈土。桶壁的内外土层未形成良好的塑性贯通区，故桶体稳定，不会无限倾覆、滑移。

5 地基极限承载力分析

在正常复合加载工况下，保持竖向荷载、弯矩不变，不断增大水平荷载直至极限，为减少计算时间，采取1/2模型，进行极限承载分析。

泥面转角与水平荷载增量及其百分数的变化关系如图11所示，当水平荷载增加1 300kN时，转角达到0.692%，曲线出现拐点(突变点)，此时可认为极限水平荷载增量为1 300kN，即在正常复合加载工况下，水平荷载可继续增大100.59%，有1 300kN 的裕量，极限值为1 292.35+1 300=2 592.35kN。

图11 泥面转角与水平荷载增量及其百分数的变化关系曲线

泥面与桶顶的水平位移随水平荷载增量变化曲线如图12所示，随着水平荷载逐渐增大，泥面水平位移曲线基本呈直线均匀变化，在水平荷载增加1 300kN 时，曲线出现拐点(突变点)。

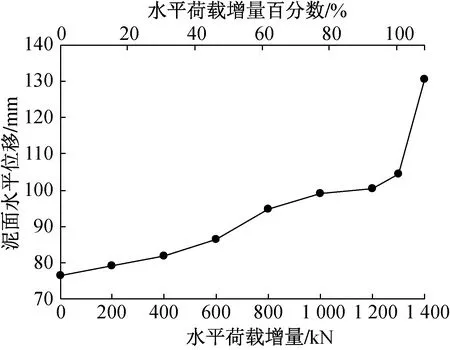
图12 泥面水平位移与水平荷载增量变化关系曲线

泥面转角与弯矩增量及其百分数的变化关系如图13所示，当弯矩增加60MN·m时，转角达到0.696%，曲线出现拐点(突变点)，此时可认为极限弯矩增量为60MN·m，即在正常复合加载工况下，弯矩还可继续增大46.48%，有60MN·m的裕量，极限值为129+60=189MN·m。

图13 泥面转角与弯矩增量及其百分数的变化关系曲线

吸力桶桶盖处的左、右侧泥面水平位移随弯矩增量的变化曲线如图14所示，随着弯矩逐渐增大，泥面水平位移曲线呈直线均匀变化，在弯矩增加60MN·m时，位移曲线出现拐点(突变点)。

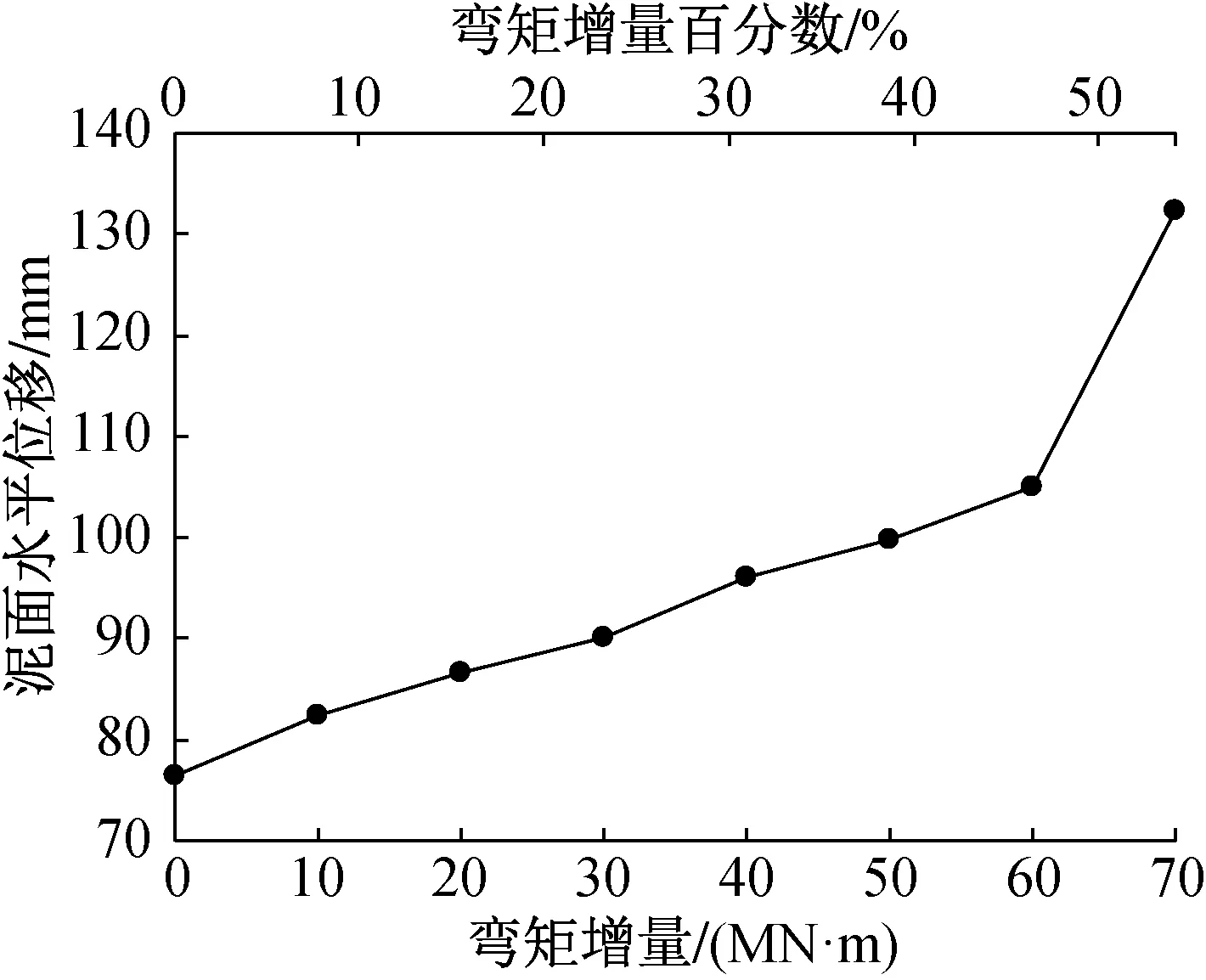
图14 泥面水平位移与弯矩增量变化关系曲线

泥面转角与竖向荷载增量及其百分数的变化关系如图15所示，当考虑上部的风机自重荷载时，泥面转角比不考虑风机自重荷载时更小，表明一定的自重荷载反而有利于提升风机的安全性。这是由于施加了竖向荷载后，桶内及底部土体受到挤压并受桶壁及分舱板的约束而变得密实，密实土体所具有的较大承载能力使得桶-土具备一体化承载模式对抵抗水平力有利。

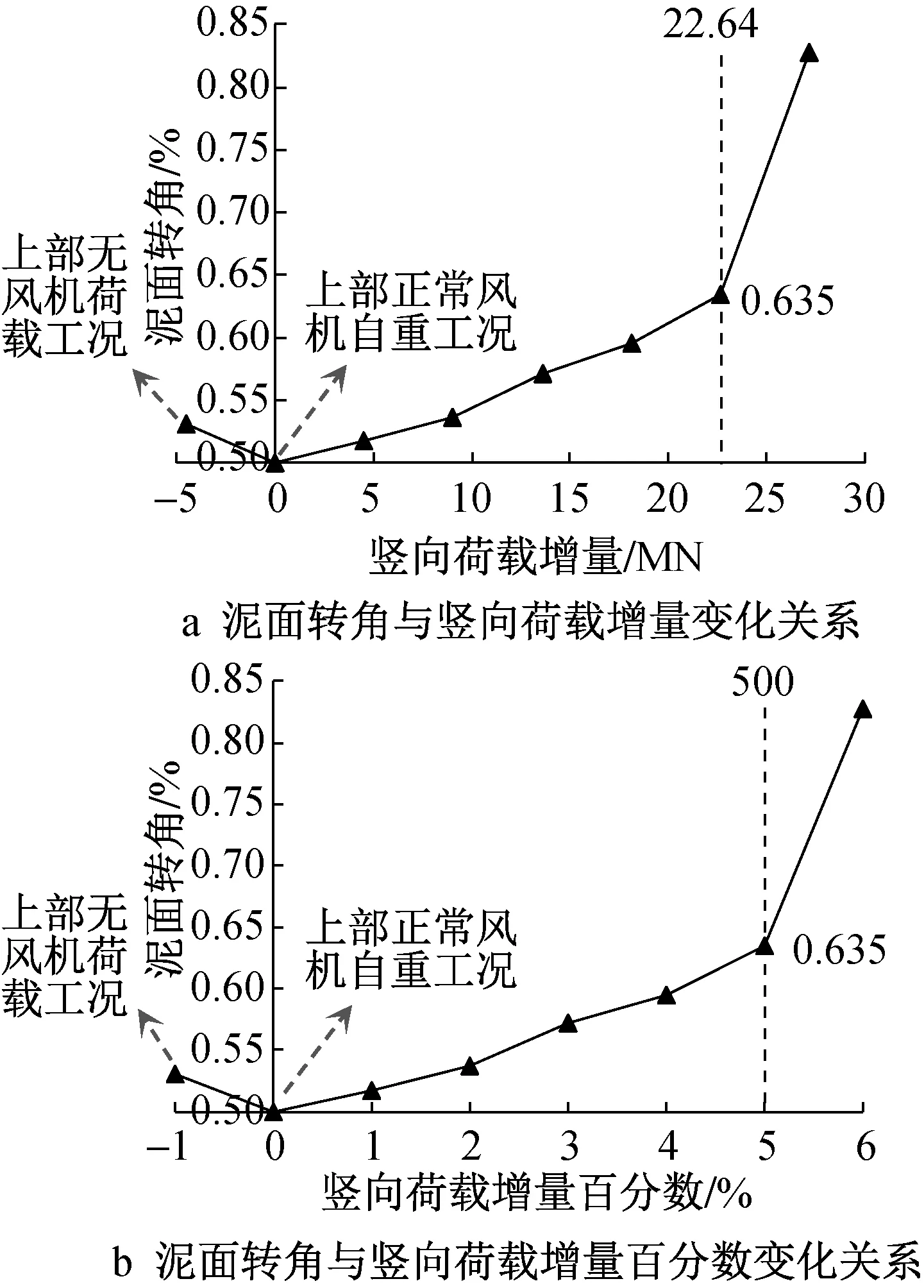
图15 泥面转角与竖向荷载增量及其百分数的变化关系曲线

在自重荷载基础上，继续逐渐增大竖向荷载，转角将逐渐增大、突变，复合桶形基础将失稳。

泥面水平位移随着竖向荷载的不断增大而增大，最终发生突变、失稳，如图16所示。

图16 泥面水平位移与竖向荷载增量变化关系曲线

6 结语

结合工程地质与荷载条件，考虑吸力桶-土相互接触，建立了实体、结构、地层的复杂三维数值模型，进行多工况、多荷载模式的变形规律与承载特性分析，得出以下结论。

1)吸力桶受力一般强度可控，均未超过材料极限，其稳定性主要受变形控制，桶体位移与泥面处转角均在安全允许范围内，整体安全。

2)根据地质条件与荷载工况，通过参数化语言建模与吸力桶全尺寸精细化设计，进行结构的变形与承载力计算，验算了桶形基础正常服役状态下的稳定性，在实际工程中可根据需要调整模型尺寸、参数，进行对比与整体稳定性验算，为基础设计提供指导。

3)经典的地基承载力计算公式无法精确计算复合加载模式下宽浅式桶形基础地基的极限承载力，通过FLAC3D有限差分法计算了桶形基础在正常运行状况下地基在不同荷载模式下的极限承载力，为失稳提供预判。