一种高低轨卫星联合到达时间被动定位技术

邢瑞阳，吴启星，翟 华

（北京跟踪与通信技术研究所，北京 100094）

0 引言

近年来，随着全球航天技术、空间互联网技术的发展，一方面空间定位技术因具有覆盖范围广、受气候影响小、目标监测直视条件良好等独特优势，受到各国的广泛关注与研究投入；另一方面，目标被动定位技术在雷达、声纳、目标跟踪、物联网等方面都起着至关重要的作用。随着空间卫星资源的逐渐丰富，如何充分发挥高低轨卫星联合定位构型的庞大定位基线优势，构建高低轨卫星一体化联合定位机制，以被动获取目标高精度位置信息，成为国内外学术研究关注热点。

分析目标被动定位的诸多方法，信号到达时间（Time-of-Arrival，TOA）方法因其精度高而被认为最常用定位方法之一。一方面，传统TOA 定位技术需要定位传感器和目标之间满足精确时间同步条件，但该条件在实际应用中很难保障；另一方面，在非合作定位场景下，因目标的不可控特性，定位传感器和目标之间时间同步不可能实现。高低轨卫星联合空间被动定位场景下，目标无法受定位系统控制而与定位传感器之间保持精确时间同步。因此，针对目标与定位传感器时钟异步的实际问题，本文研究基于高低轨卫星联合TOA 测量的被动定位算法。

在高低轨卫星联合定位系统内，若定位卫星和目标之间不满足时钟同步条件，将引入一个额外参数，称为目标信号起始传输时间。一种处理方法便是选择某卫星的TOA 测量值为参考量，在参考量和其他卫星的TOA 测量值之间做减法得到到达时间差（Time Difference of Arrival，TDOA）测量值，但该方法使得定位解析方程非线性关系更加复杂，且会受高低轨定位卫星构型严重影响，使得问题更加难以解决。另一种处理方法是对目标位置与未知起始传输时间进行联合估计。例如，XU 等提出了利用半正定松弛（Semi-Definite Relaxation，SDR）技术将定位问题松弛为一个凸半定规划（Semi-Definite Program，SDP）问题，通过对不同目标函数求最小值的方法，提出了2 步最小二乘算法和最小-最大算法，由于求解过程中的近似和松弛，这2 种算法都有一定性能损失。WANG 等通过最小化噪声项的ℓ范数和ℓ范数，提出了2 种二阶锥松弛（Second-Order Cone Relaxation，SOCR）方法，由于求解过程中进行了松弛操作，这些方法也无法达到克拉美罗下界（Cramer-Rao Lower Bound，CRLB）精度。GAO 等将SOCR 方法扩展到具有非视距误差的定位场景。VAGHEFI提出了一种不同的SDR 方法，将SDR 应用于最大似然（Maximum Likelihood，ML）问题，但该方法无法达到ML问题最优解和CRLB精度。ZOU等通过增 加二阶约束和惩罚项，对文献［10］中的松弛SDP 问题进行了约束，在提高算法的性能的同时也增加了计算复杂度。YAN等提出了一种使用量化TOA测量来减少通信开销的SDR 方法，该方法也使用了未知起始传输时间的类似模型。

此外，目标被动定位问题需要确切可知传感器确切位置坐标，且要求不同传感器之间保持高精度时钟同步，但在很多实际应用中，这两点要求往往很难满足。在高低轨联合定位系统中，低轨卫星高速运动特性使其在特定采样时刻的位置与速度信息存在一定误差，且高低轨不同卫星由于初始设计目的与方案存在差异性，使其之间不可避免地存在一定时统误差。在此，我们将卫星星历误差与时钟同步误差统一称为系统误差。国内外诸多文献已证明，较小的系统误差都会严重恶化目标定位精度，这种情况下，定位算法需将定位传感器系统误差统计知识考虑进来以提升定位精度。

针对上述问题，本文提出一种面向高低轨卫星联合目标被动定位的SDR 方法，以达到存在误差情况下提升系统性能的目的。本文在模型构建中针对时钟同步误差和卫星位置误差分别设置参数，在算法解算中首先优化求解误差参数，然后完成目标定位，并通过仿真证明了本文方法在误差条件下提高系统性能的有效性。与文献［7］和文献［10-11］中采用的SDR 方法不同的是，本文所提出松弛SDP 问题在理论上始终是紧的，从而保证了算法具有良好定位解析收敛性能。首先，所提新方法对被动定位测量模型进行变换，在变换后测量模型基础上提出加权最小二乘（Weighted Least Squares，WLS）问题；继而，将SDR 技术应用到WLS 问题中，得到一个松弛SDP 问题，从理论上讲，松弛SDP 问题总是紧的，因此它的最优解总是满足原始WLS 问题解；然后，在此基础上，将所提方法扩展到运动目标定位场景。具体而言，假设目标速度在足够小观测周期内为常数，以联合估计目标初始位置、运动速度和未知起始传输时间。从理论上讲，虽然该场景下松弛SDP 问题可能并不紧，但仿真结果表明，本文所采用的非凸问题简化方法可在很大程度上保证松弛中的秩1 条件，除非测量误差非常大或卫星数目非常少，否则松弛SDP 问题仍然是紧的，即本文方法针对运动目标在该场景下仍具有良好解析性能。

本文中，黑体小写字母为向量，黑体大写字母为矩阵。为矩阵的第行第列的元素，为矩阵中从 第行至第行、从第列至第列元素组成的子矩阵，tr()和rank()分别为矩阵的迹和矩阵的秩，≽0 为矩阵半正定。

1 高低轨卫星联合被动定位模型

1.1 静止目标情况

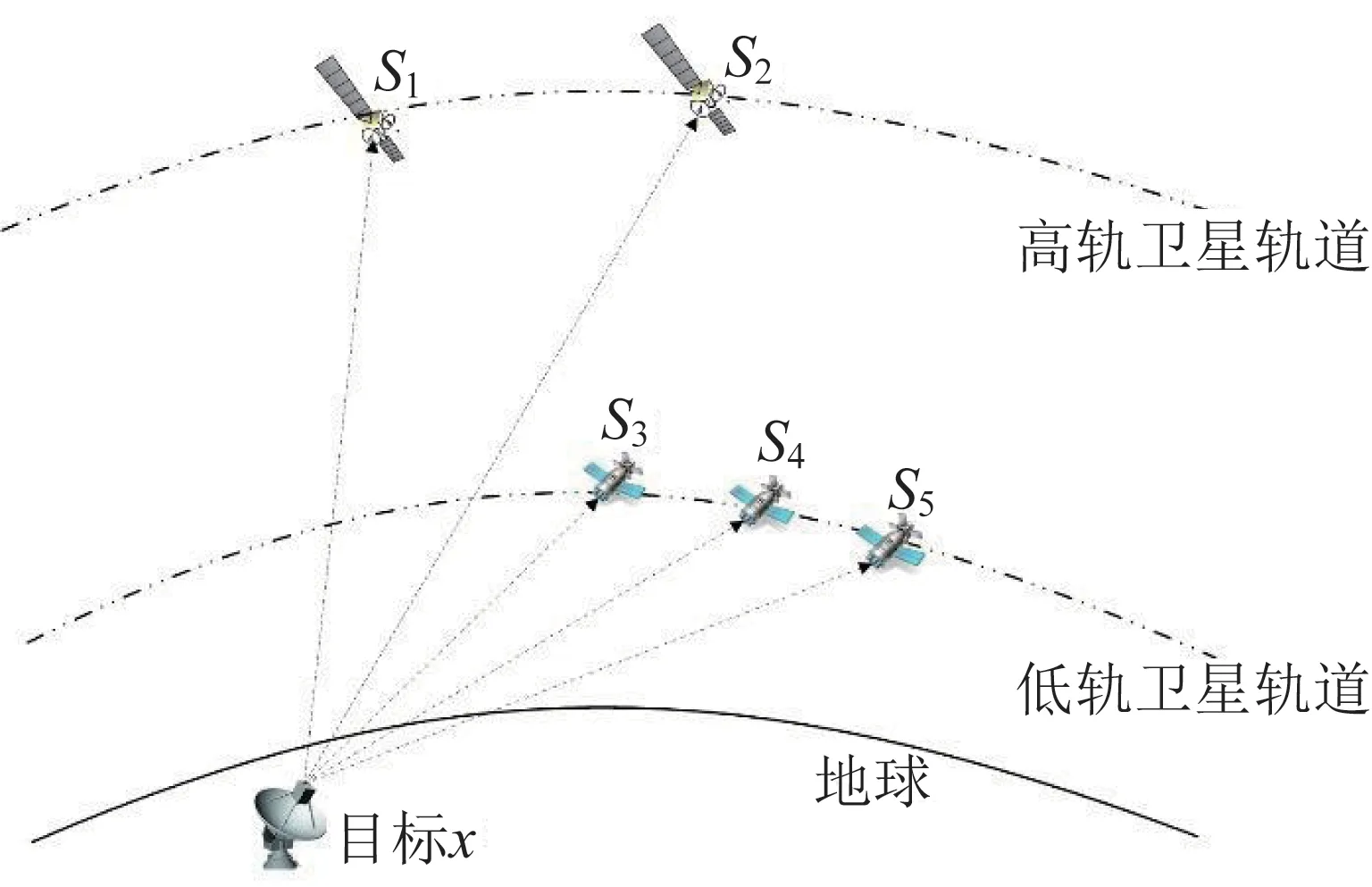
图1 基于高低轨卫星联合的TOA 被动定位模型Fig.1 Schematic diagram of the passive localization model by low and high orbit satellites based on TOA

式中：Δs为第个卫星位置误差。

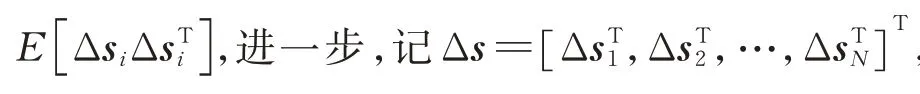
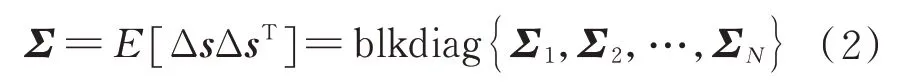
式中：blkdiag 为块对角矩阵。

不考虑卫星系统误差时，含有未知起始传输时间的TOA 测量模型可以表示为

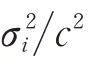
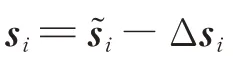
两边同乘以得到第个卫星与目标之间距离测量值为

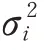
对式（5）作关于Δs的ℓ范数泰勒展开有

若令=[，，…，ε]，则误差 向量的协方差矩阵为

根据式（6），和的最大似然ML 估计可表示为

显然，该问题是非凸的，如果没有良好的初始解为保障，很难保证解析过程得到其全局最优解。

1.2 运动目标情况

将静止目标的高低轨卫星联合定位模型推广至运动目标情况，假设某目标在足够小观测时间内以恒定速度运动，其在时刻的位置用x表示，即

式中：为目标初始位置；为运动速度；为采样周期；为观测总次数。当目标移动缓慢或采样周期足够小时，假设速度恒定是成立的。

根据式（8），不考虑卫星系统误差时，定位卫星与目标之间距离测量模型可表示为

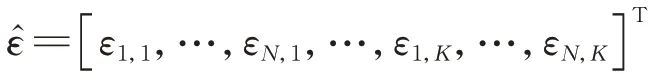
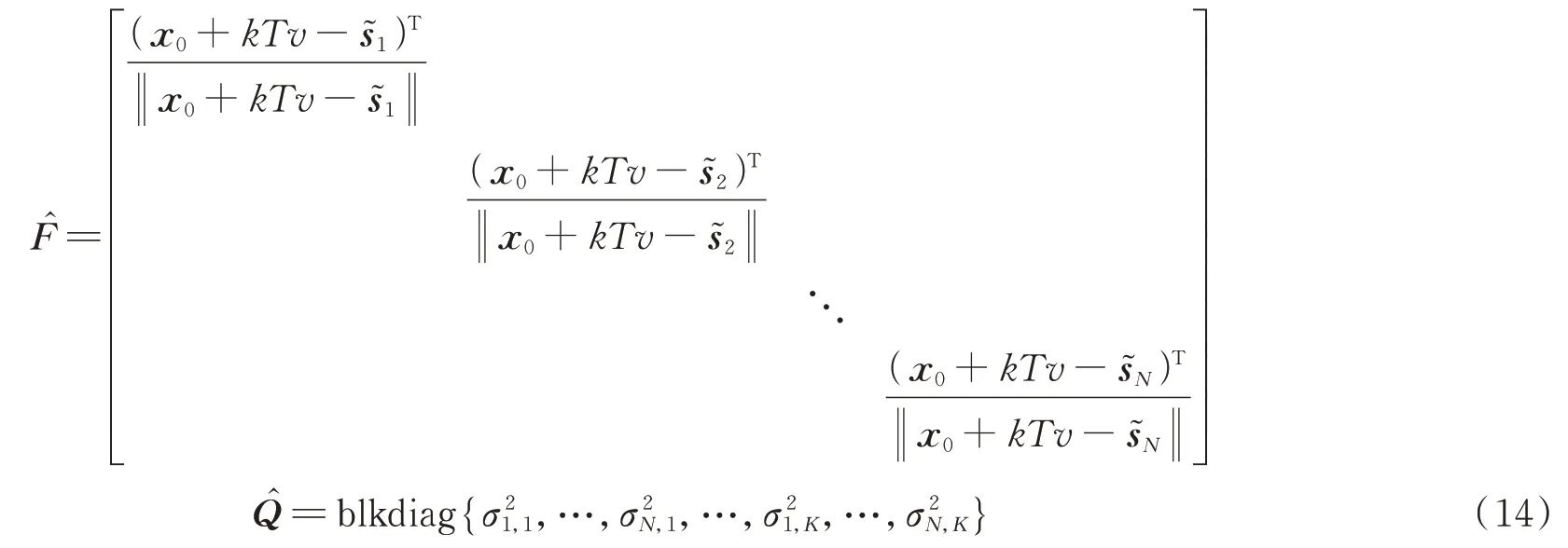
将式（10）等价转化为

与静止目标定位场景类似，运动目标定位的最大似然ML 估计可表示为

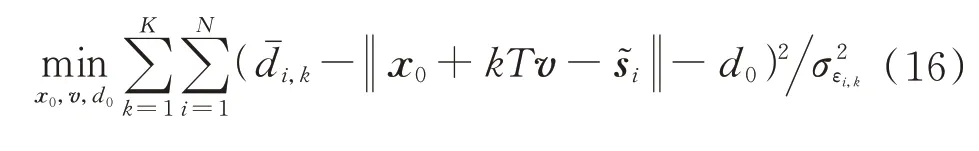
2 基于SDR 的被动目标定位算法

在本章中，首先提出用于静止目标被动定位的SDR 方法，然后将其扩展到运动目标被动定位场景。

2.1 静止目标定位场景

在到达距离测量模型（6）中，将+ε移到左边，然后两边平方，有

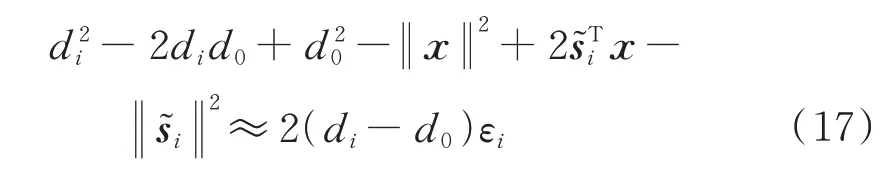
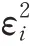
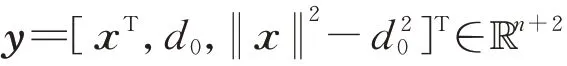
根据式（14），得到以下WLS 问题：

式中：=BQ B。

将式（15）写成以为变量的优化问题，即

在问题（16）中，目标函数关于是线性的，唯一的非凸约束是秩1 约束。去掉式（16）中的秩1 约束，得到凸SDP 问题：

权重包含未知参数=/。在实际应用中，我们首先将设为Q来求解问题（17），得到的初始解，然后将的初始解代入，再次求解问题（17），得到目标位置最终估计。需注意，算法性能通常对加权矩阵的近似不敏感。

将SDP 问题（17）的解表示为，的秩表示为ℓ。根据文献［26］，ℓ 取决于等式约束的个数，具体来说，它们的关系满足ℓ(ℓ+1)≤2。可见问题（17）有两个等式约束（即=2），这就意味着问题（17）的最优解总是秩为1 的。因此，松弛后的SDP 问题总是紧的，而WLS 问题（15）的最优解总是可以通过=(从SDP 解中得到。相应地，可以通过=得到目标位置估计。

2.2 运动目标定位场景

与静止目标定位场景类似，由式（11）得

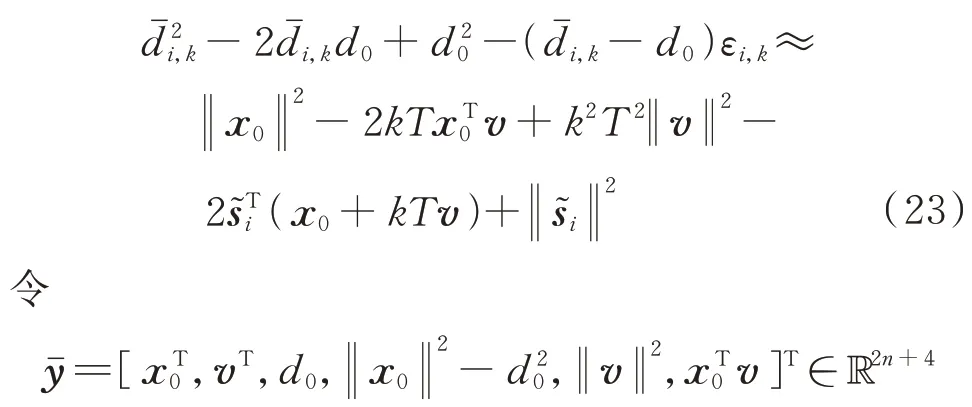
将式（18）写成如下矩阵形式：

类似地，去掉秩1 约束得到以下凸SDP：

由式（21）可得目标初始位置和速度分别为

与静止目标定位场景不同，运动目标定位的松驰SDP 问题可能无法保证秩1 解。然而，第4 章的仿真结果表明，在非极度恶劣噪声水平下，该SDP问题仍然可以得到秩1 解，这意味着所提的SDP 方法可推广应用于运动目标的场景。

3 计算机仿真结果与性能分析

本章将通过仿真来验证本文所提算法性能（用“SDP”表示），静止目标和运动目标均进行了测试分析。针对静止目标定位场景，还验证了二阶锥规划（Second-Order Cone Programming，SOCP）方法性能。在2 种情况下，分别跟MLE 性能和CRLB 性能进行了对比。SDP 和SOCP 由CVX 工具箱的SeDuMi进行求解；以起始传播时间真值与SDP算法解得目标位置结果为初始值，MLE 问题利用Matlab 中的snowline 函数求解，并选择代价函数值较小的解作为MLE 问题的最终解。

各种算法的性能采用均方根误差（Root Mean Squared Error，RMSE）为标准进行评价，其定义为

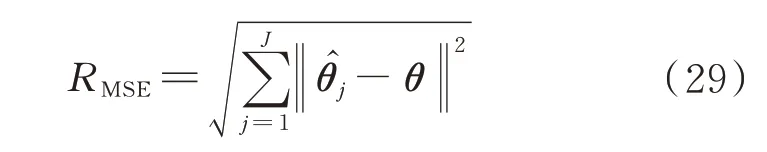
3.1 静止目标定位场景

为充分验证本文所提算法针对静止目标定位性能，所定义地心地固坐标系下定位场景见表1。

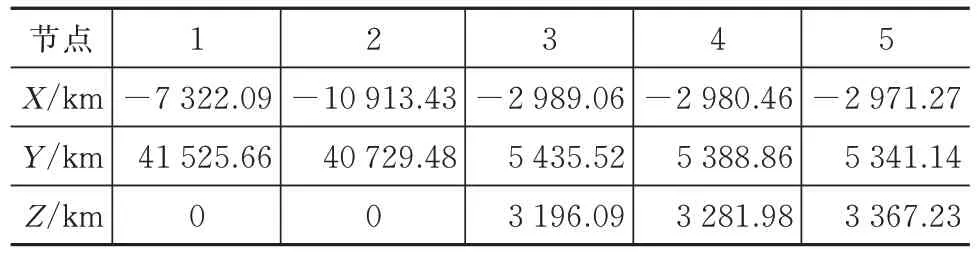
表1 地心地固坐标系下定位节点位置坐标Tab.1 Location coordinates of the localization nodes in the earth-centered solid coordinate system

首先仿真验证5颗高低轨卫星数目联合，=9 m，距离测量误差方差在10～10m变化时本文所提算法性能结果如图2 所示。可以看出，所提算法始终能够达到CRLB 精度和极大似然估计（Maximum Likelihood Estimate，MLE）算法精度，而SOCP 方法即使在噪声非常小的误差情况下也不能达到CRLB 精度，这主要归因于本文所提出SDP算法总是能够得到一个秩1 解。因此，本文所提算法通过首先优化求解时钟同步误差，并采用凸松弛方法解算定位方程，可实现误差条件下高低轨卫星联合TOA 高精度定位，有效提升了存在误差情况下系统的定位性能。

图2 各算法随测量噪声变化的RMSE 比较（静止目标定位场景）Fig.2 RMSE comparison of different algorithms with the measurement noise （stationary target localization scenario）

3.2 运动目标定位场景

与静止目标定位场景相似，本节对距离测量噪声变化情况进行仿真验证。同样选择上述5 颗高低轨卫星，=9 m，总观测次数=6，目标位置估计和速度估计结果均方根误差如图3 所示。从图中可以看出，本文所提出的SDP 方法在噪声较大的情况下仍能达到CRLB 性能和MLE 算法精度。

图3 各算法随测量噪声变化时的RMSE 比较（运动目标定位场景）Fig.3 RMSE comparison of different algorithms with the measurement noise （moving target localization scenario）

为了进一步研究估计性能，本文还仿真验证了当距离测量噪声方差为=10m时，SDP 和MLE 方法目标位置和速度估计误差的累积分布函数（Cumulative Distribution Function，CDF）的仿真验证，结果如图4 所示。

图4 当σ2=102.5 m2 时算法随信源位置和速度估计误差变化CDFs 对比（运动目标定位场景）Fig.4 CDF comparison of different algorithms with the source location and velocity estimation error when σ2=102.5 m2（moving target localization scenario）

可以看出，与MLE 方法相比，SDP 方法80%以上的目标位置估计误差在量级上与MLE 算法具有可比性，这也从侧面说明即使在噪声较大的情况下SDP 方法性能依然良好。此外，SDP 方法比MLE方法在目标速度估计方面的性能较优。

此外，验证了本文所采用的非凸问题简化方法能否满足秩1 条件的情况，当以5 为步长，从0 到40 变化，每次进行1 000 次运算，仿真结果显示每次仿真均能达到1 000 次秩1 条件。可见，在噪声较小情况下，由于本文所采用的非凸问题简化方法可在很大程度上保证松弛中的秩1 条件，尽管理论上不能保证得到秩1 解，所提方法可以得到秩1 解，这进一步验证了所提方法的可靠性。

4 结束语

本文以高低轨卫星联合定位为背景，针对未知初始传输时间的TOA 定位问题，考虑卫星位置误差与时统误差等系统误差的情况下，提出了一种基于SDR 的定位方法。通过建立非凸WLS 最小化问题，将未知初始传输时间引起的距离偏差与目标位置、速度未知量进行联合估计，然后应用SDR 算法求解。仿真结果表明，尽管在求解过程中进行了近似和松弛，在高低轨卫星联合定位场景下，该方法仍能达到CRLB 精度和MLE 算法精度。