基于序列凸优化的上面级远程交会轨迹优化

王访寒，周如好，余薛浩，黄 飞，陈海朋

（上海航天控制技术研究所，上海 201109）

0 引言

上面级是航天运输系统的重要组成部分之一。与基础级火箭相比，上面级具有多次启动、长期在轨、自主飞行、轨道机动能力强等特点，工作时通常已经进入地球轨道，具备较强的灵活性和通用性，可以适应多种不同的任务情况。近年来，随着在轨服务需求的不断增加，上面级将继续向着自主化、智能化等方向发展，其中自主交会和轨迹优化是其中的关键技术，也是研究的热点问题。

目前常见的轨道优化方法有采用庞特里亚金极小值原理的间接法、以高斯伪谱法为代表的直接法、以遗传算法为代表的智能算法等。间接法将轨迹优化问题转化为哈密顿边值问题，但是存在推导过程复杂、协态变量初始值难以估计等问题。在此基础上发展出的直接法将问题转化为非线性规划问题，对初始猜测不敏感，但是计算量较大，常用于离线轨迹规划。还有智能算法同样具有计算耗时较长、实时性差等问题。

在诸多轨道优化方法中，凸优化方法在实时性方面具有非常明显的优势。尤其是对偶内点法的发现，可以确保二阶锥规划问题在有限步迭代内收敛到最优解。ACIKMESE 等将凸优化技术成功运用于火星登陆器软着陆的最优控制问题。LIU 和LU 等采用无损凸化的方法将交会对接中的非凸问题转化为凸问题并求出优化轨迹。WANG 等采用角度而非时间作为自变量，求解了小推力航天器轨道转移问题。林晓辉等基于凸优化研究了月球精确定点软着陆问题。李鑫等基于序列凸优化求解了固定时间远程交会问题。池贤彬等运用凸优化制导技术研究了近程自主交会问题。

目前，相关文献中还有一些待解决的问题。首先，研究大多是基于固定时间假设求解燃料最优问题，并未说明如何确定轨道转移所用的时间，在没有时间限制的常规交会任务中，如果给定的时间过长或过短，则优化出的轨迹并不是真正意义的燃料最优；其次，在空间救援或目标监视等紧急的特殊任务中，会要求上面级在燃料约束下用最短时间与目标器完成交会，此时固定时间的轨迹优化方法不再适用；最后，现有文献对迭代初始值的猜测缺乏详细说明，一般是采用初位置与末位置的线性插值作为位置的初始猜测，虽然序列凸优化具有对初值不敏感的优点，但是在上面级大范围轨道转移的情况下，这种偏差较大的初值在某些情况下会对收敛性产生一定影响，所以需要一个较为接近实际情况的初值来保证收敛性，加快收敛速度。

针对以上问题，本文采用地心距代替时间作为自变量，建立了末端时间自由的上面级远程交会模型，并采用Lambert 双脉冲变轨的计算结果作为迭代初值，最后在时间最优和燃料最优两种任务情况下进行了仿真验证，求出了两种情况下的最优轨迹和推力控制序列。

1 基于凸优化的上面级远程交会模型

1.1 问题建模

本文针对末端时间自由的共面圆轨道远程交会问题进行研究，为便于问题描述，建立了极坐标系，如图1 所示。

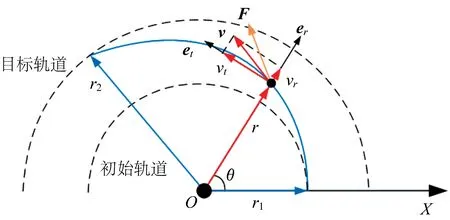
图1 轨道转移极坐标系示意图Fig.1 Polar coordinates for orbital transfer

图1 中：轴方向为地心指向上面级初始位置；为上面级绕地心飞过的角度；为上面级位置矢量；为上面级初始轨道半径；为目标器轨道半径；为推力矢量；为速度矢量；v和v分别为径向速度分量和切向速度分量。以时间为自变量的传统动力学方程为

式中：为上面级到地心的距离；为发动机总推力大小；F和F分别为发动机总推力在径向和切向的分量；为地球引力常数；为发动机喷气速度。

以时间作为自变量常用于固定时间下燃料最优问题，而对于末端时间自由的远程交会问题，一种做法是内层采用固定时间的传统优化方法，外层采用二分法或智能算法对最优时间进行搜索，这种方法没有真正意义上将时间作为优化变量加入到模型中，每一次外层搜索都进行了一次固定时间的轨迹优化，会大大增加总计算时间，无法应用于线上计算。

另一种做法是利用归一化将时间变换到区间[0，1]，再当成固定时间问题进行求解。然而这种方法会导致末端时间这一未知量始终存在，后续的问题凸化将变得十分困难。同理，转移角度在末端时间自由的交会问题中也不适合作为自变量。造成这一问题的根源为：当末端时间不固定时，时间和转移角度都没有一个确定的上界，模型离散化后待求向量的维数无法确定，导致无法求解。

为解决上述问题，本文采用上面级到地心的距离作为自变量，在径向速度不小于零的前提下，的取值范围为[，]且单调，把时间作为待优化变量加入到模型中，利用时间与地心距的关系改写动力学方程如下：

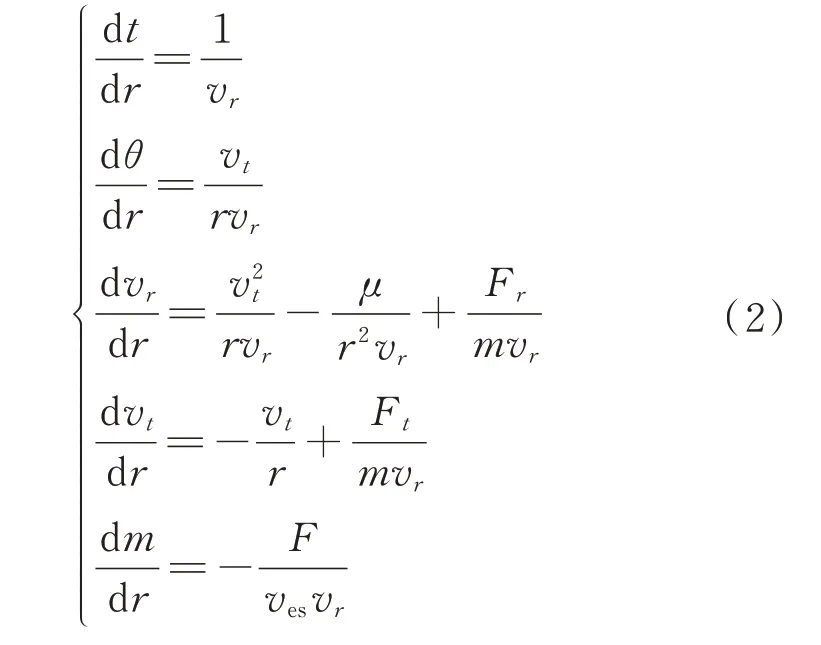
应满足的初始条件为

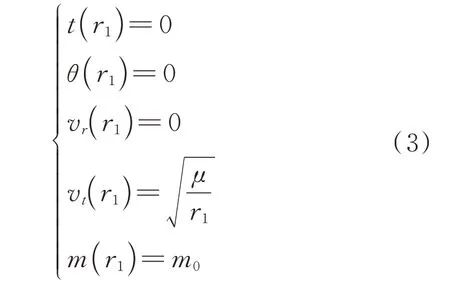
式中：为上面级初始质量。

应满足的末端条件为

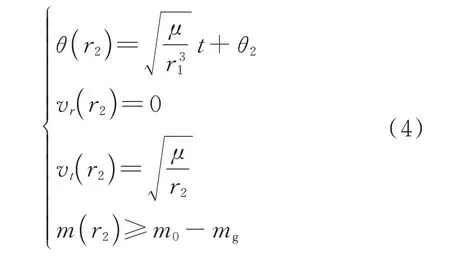
式中：为目标器初始相位角；为远程交会可用燃料质量。此外，还可以根据任务需求增加时间约束。

基于有限推力的控制约束为

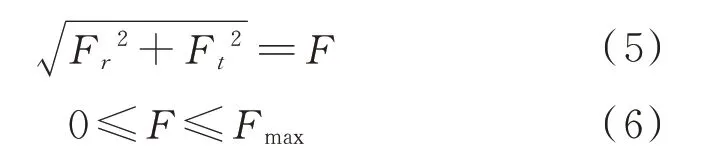
式中：为发动机最大推力。

优化指标可表示为

式中：和分别为交会时间和燃料消耗的加权因子；Δ和Δ分别为轨道转移所用时间和消耗燃料质量。当=0 且=1 时，燃料最优；当=1 且=0 时，时间最优。

此外，还应根据实际任务需要，将变量约束在一个大致合理的范围内，同时用小量代替约束条件中径向速度为0 的情况，以避免出现奇异问题。

1.2 模型转化

若想应用凸优化解决该问题，就需要将原始问题中的非凸部分进行凸化。上述模型中的非凸项主要存在于动力学中的速度位置、质量变化和推力约束。

首先，为消除质量变化产生的非凸部分，定义新变量如下：

对式（9）两边同时对半径求导得

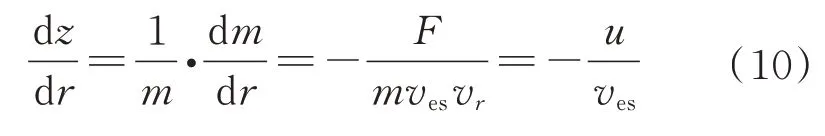
由式（10）可以看到，用变量代替质量，并用代替了/项，消除了原模型中质量变化造成的非线性部分。

其次，为消除推力约束产生的非凸部分，定义新变量：

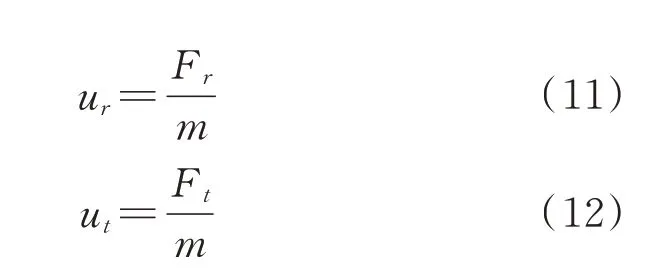
则式（5）和式（6）所表示有限推力约束可写为

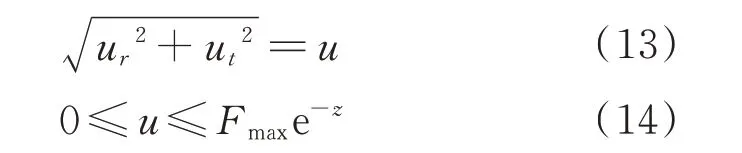
式（13）～式（14）中表示的推力约束在三维空间中是一个二阶锥的表面，是非凸的，通过无损松弛将其转化成凸约束，在三维空间中表示实心二阶锥，如图2 所示。

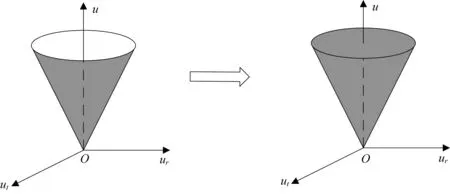
图2 控制约束无损凸化Fig.2 Lossless convexification of control constraint

无损松弛后式（13）改写为

将式（14）右侧在参考轨迹z处泰勒展开，取一阶近似得

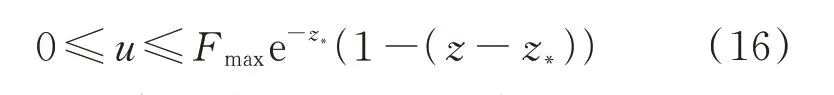
最后，通过序列线性化的方法来处理动力学中剩余的非凸部分，经过1.1 节中的变量替换后，动力学方程的形式为

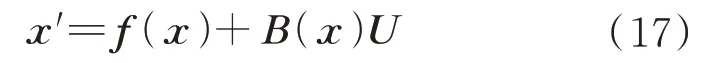
式 中：=[，，v，v，]为状态变量；=[u，u，]为控制变量。向量()和矩阵()的表达式为

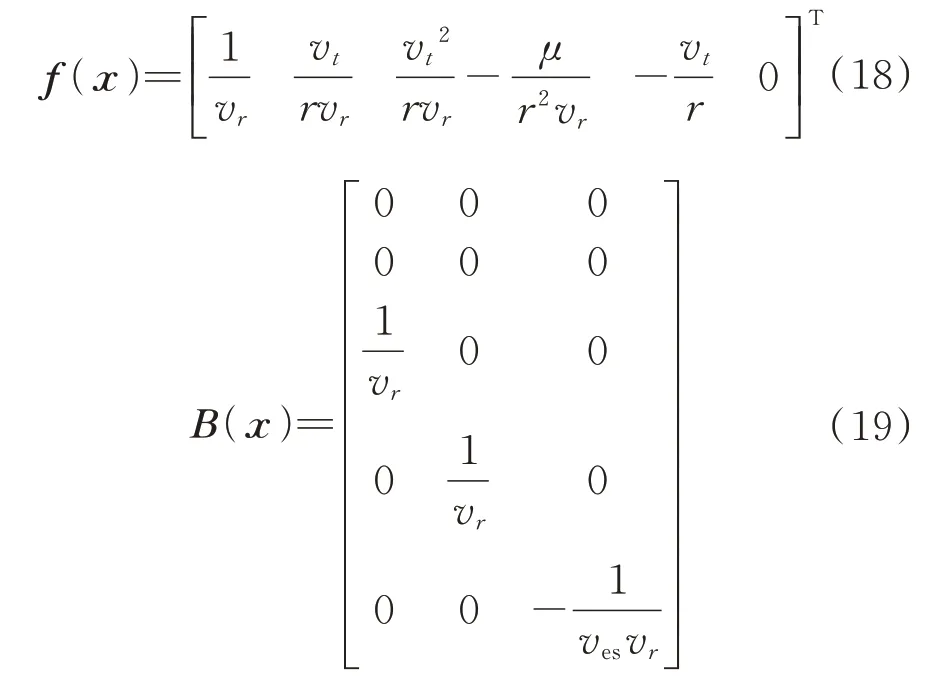
假设上一次迭代后产生轨迹的状态变量为，则动力学方程线性化后可近似为

至此已将原模型中所有非凸部分凸化，记第次迭代的状态向量为，使用一阶差分进行离散化处理，步长即采样距离设为R，该问题转化后的最终形式为

2 迭代算法设计

进行序列凸优化的迭代求解需要初始参考轨迹，一般是采用初末位置线性插值的方法给出初始轨迹。虽然序列凸优化具有对初值不敏感的优点，但是一个合理的初值可以保证收敛性，减少迭代次数，增加算法实时性。本文结合上面级发动机推力较大的特点，采用Lambert 双脉冲转移轨道作为初始参考。由于Lambert 法已有成熟的求解步骤，在固定时间条件下可快速求解出转移轨道，相关文献已有详细研究，此处不再赘述。

求解序列凸优化的算法步骤如下：

给定脉冲轨道转移时间，利用Lambert法计算出脉冲转移轨道作为初始猜测。

初始化：令=0，根据初始猜测的转移轨道，计算出，进而求出()、()、()的值。

当≥1 时，利用对偶内点法求解式（23）～式（24）表示的凸优化问题，得到优化后的轨迹和控制向量。

判断所求轨迹是否满足收敛条件，收敛条件如下：

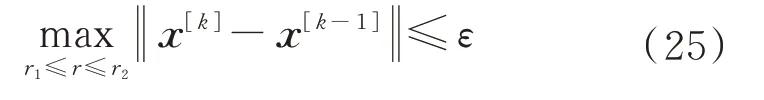
式中：为允许误差。若满足条件则执行步骤6，若不满足条件则执行步骤5。

利用求得的轨迹更新()、()、()的值，并执行步骤3。

所求的最优轨迹和控制向量为和。

算法流程如图3 所示。

图3 序列凸优化算法流程Fig.3 Flow chart of the sequential convex optimization algorithm

3 仿真试验及结果分析

本文针对末端时间自由的上面级远程交会问题进行仿真，以验证提出的序列凸优化算法的有效性。仿真使用的计算机配置为：CPU i5-7500@3.4 GHz，4 GB 内存，在Matlab 环境中使用CVX 工具箱求解迭代中的单次凸优化问题。

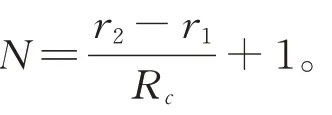
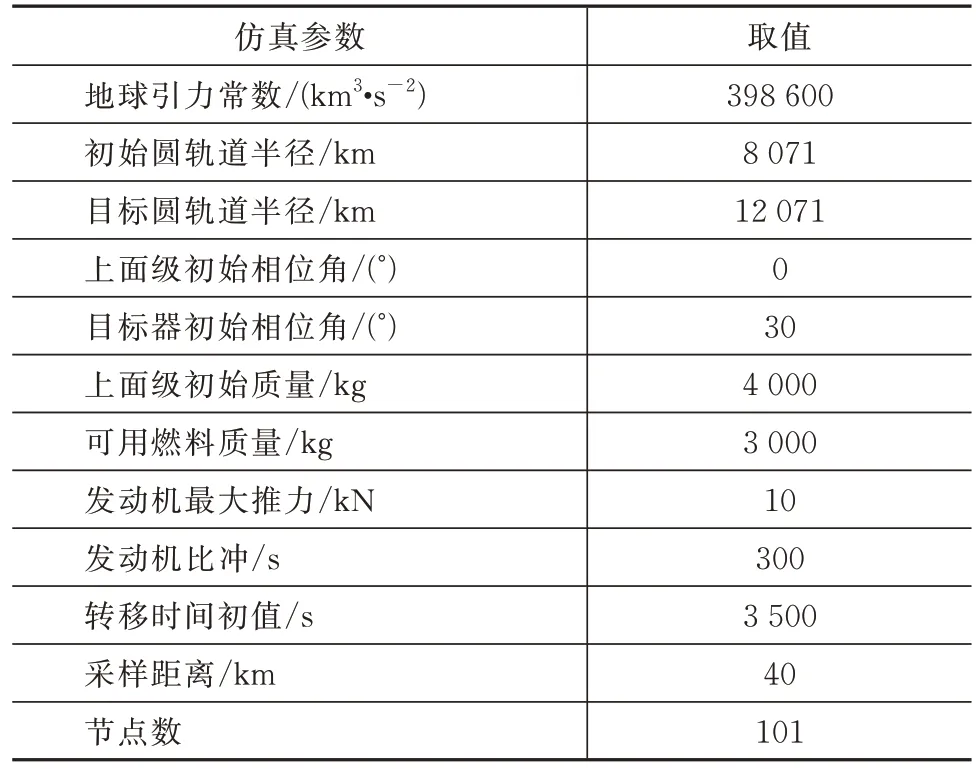
表1 仿真参数表Tab.1 Simulation parameters

优化目标参考式（23），针对燃料约束下时间最优和时间约束下燃料最优两种情况进行仿真。首先令=0，=1，即时间最优。仿真结果如下，最优轨迹如图4 所示。

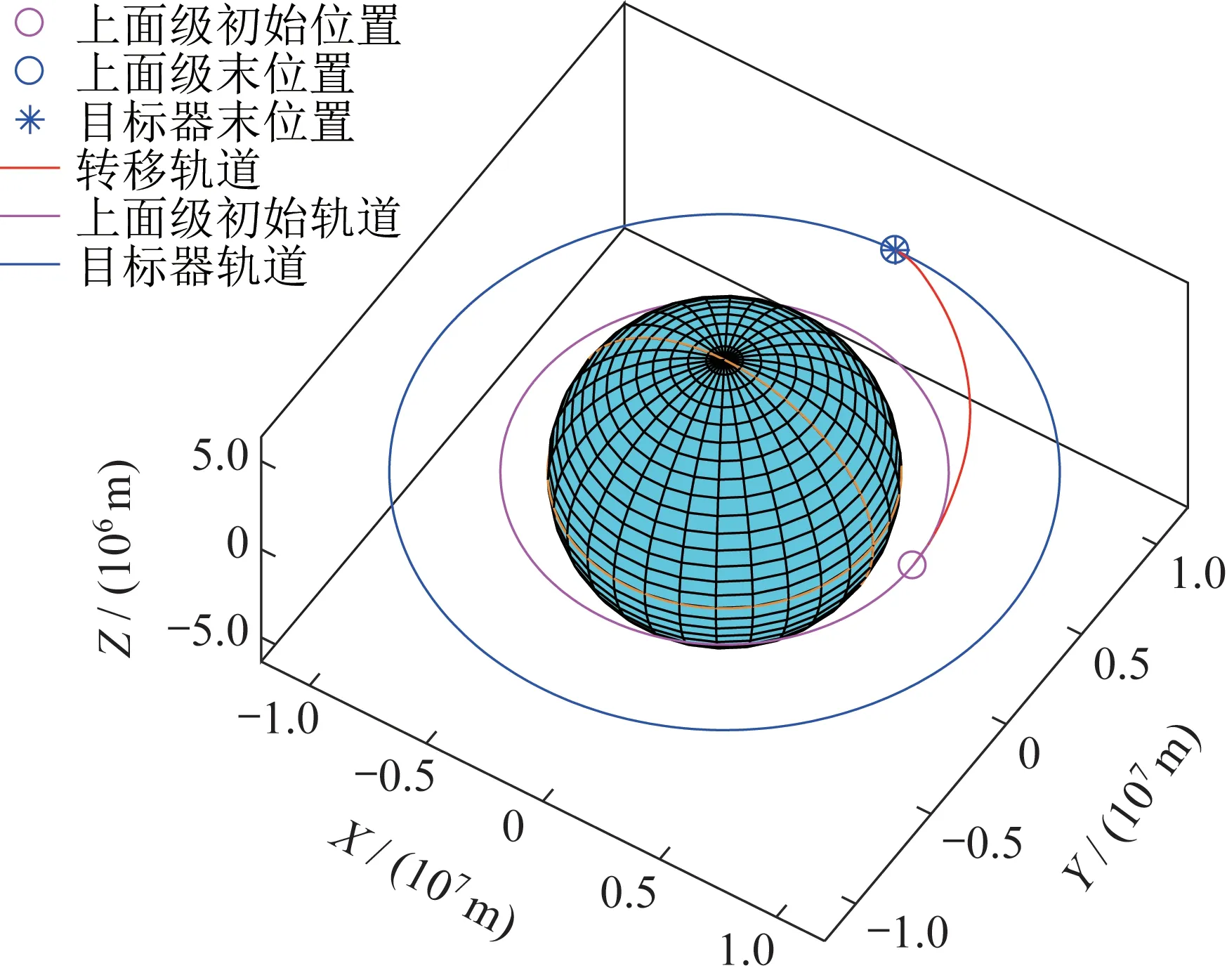
图4 时间最优交会轨迹（k1=0，k2=1）Fig.4 Minimum time rendezvous trajectory when k1=0 and k2=1

推力变化曲线如图5～图7 所示，可以看出总推力呈现典型的bang-bang 形态。目标函数的优化过程如图8 所示，算法经过12 次迭代后收敛，最终转移时间为2 426 s。质量变化曲线如图9 所示，可以看到在时间最优的情况下，上面级可用燃料被全部耗尽，剩余质量1 000 kg。由所求推力序列及上面级初始位置速度进行轨道外推，可得最终位置与目标器相差149 km，为最终轨道半径的1.23%，证明了该算法的有效性。

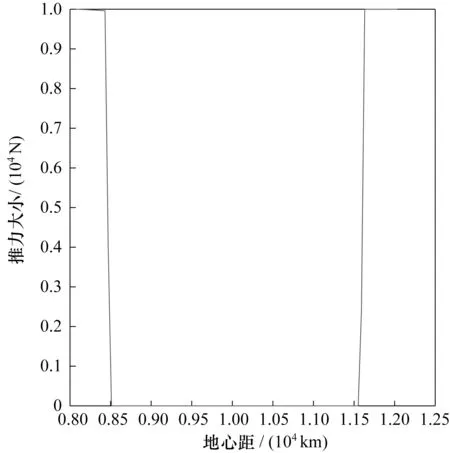
图5 总推力变化（k1=0，k2=1）Fig.5 Variation of the total thrust when k1=0 and k2=1

图6 切向推力变化（k1=0，k2=1）Fig.6 Variation of the tangential thrust when k1=0 and k2=1

图7 径向推力变化（k1=0，k2=1）Fig.7 Variation of the radial thrust when k1=0 and k2=1

图8 轨道转移时间优化过程（k1=0，k2=1）Fig.8 Optimization process of the orbital transfer time when k1=0 and k2=1

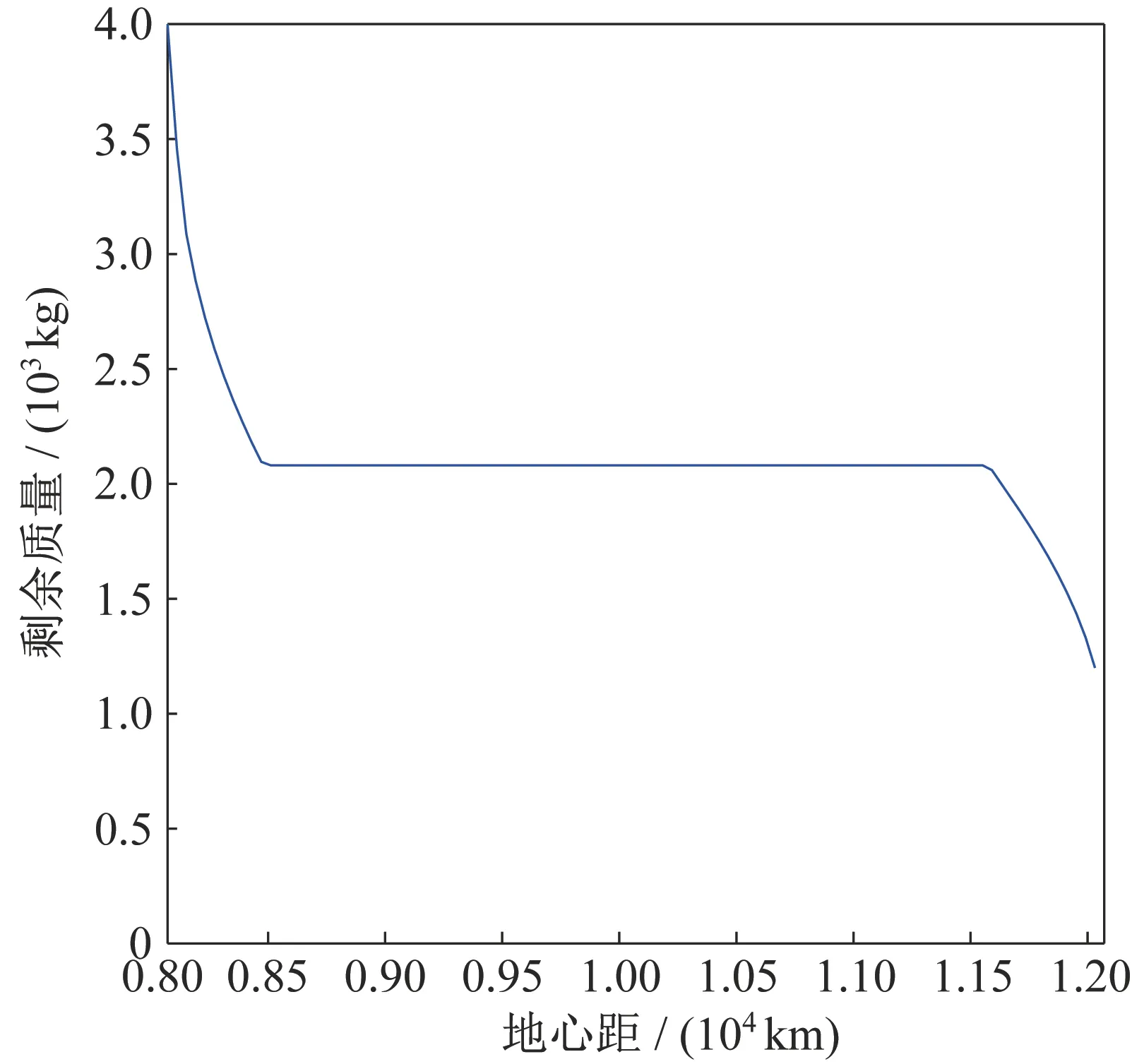
图9 质量变化（k1=0，k2=1）Fig.9 Variation of the mass when k1=0 and k2=1

下面进行燃料最优情况下的仿真，令=1，=0，仿真结果如下：燃料最优、时间最优和3 500 s双脉冲转移三条轨迹的对比图如图10 所示，可见燃料最优轨迹已经接近霍曼转移。推力变化曲线如图11 所示，总推力仍然为bang-bang 形态。上面级质量变化示意图如图12 所示，最终剩余质量为2 010 kg。燃料最优情况下最终转移时间为4 735 s。

图10 3 种优化轨迹示意图（k1=1，k2=0）Fig.10 Three optimized trajectories when k1=1 and k2=0

图11 总推力变化（k1=1，k2=0）Fig.11 Variation of the total thrust when k1=1 and k2=0

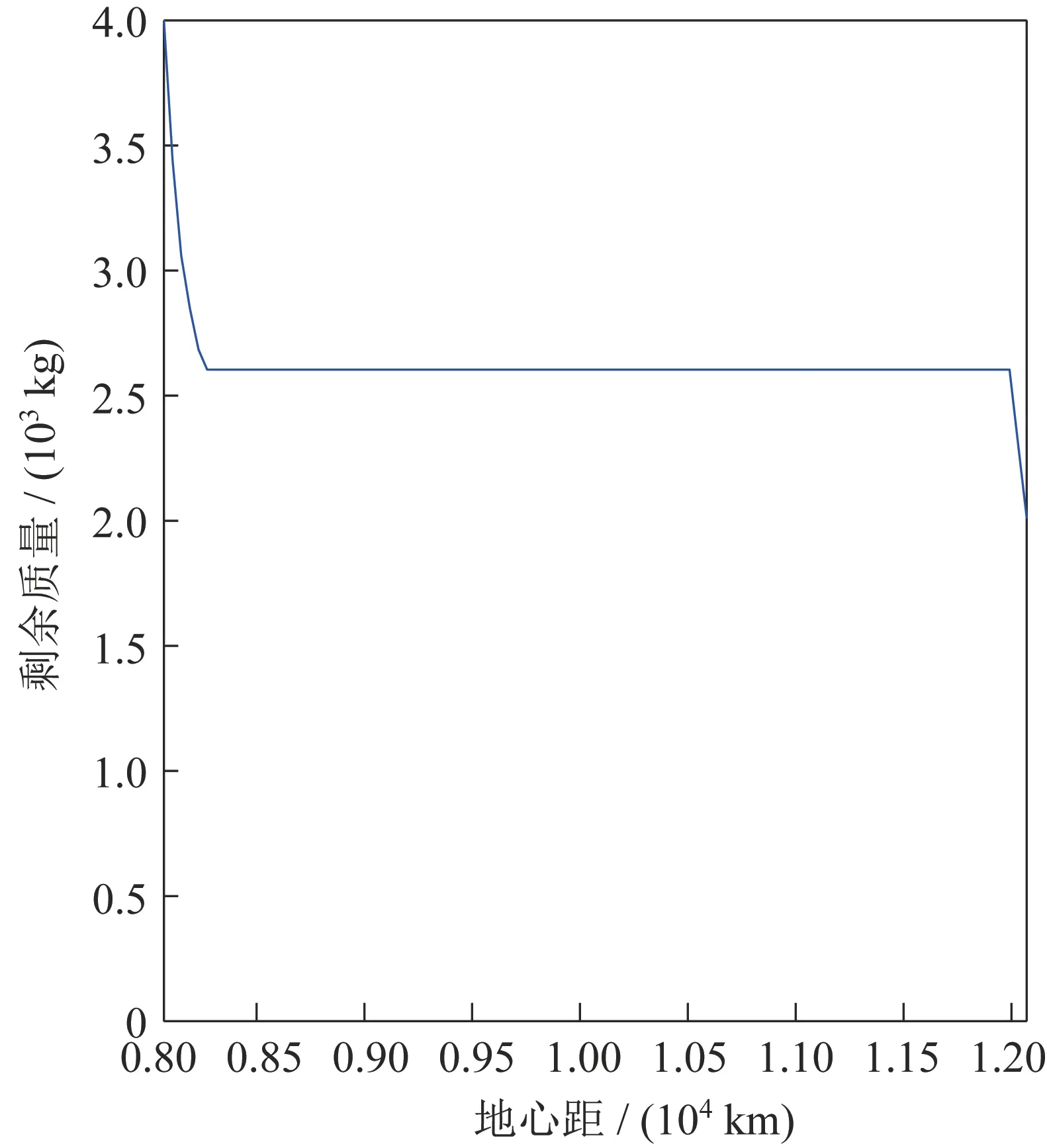
图12 质量变化（k1=1，k2=0）Fig.12 Variation of the mass when k1=1 and k2=0

通过2 种情况的对比可以看到，本文所建立模型不局限于时间或燃料的单一优化目标，可以应对多种任务情况。利用CVX 工具箱求解单次凸优化问题耗时约2 s，该计算时间与离散化的节点数量有关，算法需要进行10～20 次迭代求出最终的轨迹。

将本文提出的序列凸优化算法与遗传算法进行对比，见表2。序列凸优化算法的耗时为28 s，遗传算法的优化速度为305 s。文献［20-21］表明伪谱法在轨迹优化中的计算耗时一般为分钟级，本文提出的序列凸优化相比于伪谱法和遗传算法具有明显的速度优势，具备线上计算的潜力。

表2 仿真结果对比Tab.2 Comparison of the simulation results

4 结束语

本文研究了基于序列凸优化的上面级远程交会轨迹优化问题。针对末端时间自由的远程交会问题，采用地心距代替时间作为自变量，通过无损凸化将问题转化为凸问题，使用Lambert 脉冲转移轨道作为迭代初值，分别求出了时间最优和燃料最优任务情况下的转移轨迹和推力序列。如果针对轨道转移问题开发定制化的求解器，单次求解凸优化问题的时间还能进一步缩小，未来可应用于在线计算。但本文未考虑摄动因素，并且模型局限于圆轨道之间的交会任务，后续研究可考虑将模型扩展至异面椭圆轨道的交会任务中。