特高压直流互感器大挠度绝缘子弹性支撑设计及研究
2022-04-27达建朴刘民慧杨洪涛罗苏南
王 强, 达建朴, 刘民慧, 杨洪涛, 罗苏南, 李 钊
(1.常州博瑞电力自动化设备有限公司,江苏 常州 213025;2.南京南瑞继保电气有限公司,南京 211100)
0 引言
随着电网容量的增大、电流电压等级的提高,对相关电力设备的绝缘要求也相应提高。其中电子式电流互感器作为智能电网的监测设备,其测量的准确性与工作的可靠性对于整个电网的监测有着至关重要的影响[1-2]。悬式绝缘子作为电流互感器的绝缘部件,其长度也随着被测对象的电流等级提高而加长,目前对于高电压等级的绝缘子长度已增加到10 m以上。由于绝缘子的长度较长,内部的环氧芯棒截面积较小,抗弯能力较弱,在户外环境使用时,易受风载和温度影响,产生较大的轴向拉力。由于硅橡胶悬式绝缘子环氧芯棒与金属法兰之间的连接采用压接工艺,若轴向拉力过大,易造成环氧芯棒与金属法兰松脱;同时较大的轴力会对绝缘子两端的固定造成困难,使其容易松脱。因此笔者对如何降低绝缘子在风载作用下的轴力进行了研究。
当电压等级较高时,其硅橡胶悬式绝缘子长度会随之加长,由于长度较大,且抗弯刚度较小,在风载作用下绝缘子的弯曲属于大挠度弯曲,因弯曲较大,轴力不可忽略。因此大挠度绝缘子在风载作用下的弯曲问题属于非线性大挠度纵横弯曲问题。目前对于细长杆的大挠度问题研究多从小变形线性理论出发,再引入非线性因子进行数值计算,理论解难以得到。为了便于计算,通常采用假设合理的挠曲线方程进行计算,以满足一定范围内的工程需求[3-6]。
为了研究绝缘子在风载作用下的轴力,笔者采用瑞利-里兹法假设的挠曲线方程,研究了绝缘子在不同约束条件下,绝缘子在风载作用下产生的轴力值,发现两端不可移动支撑会产生较大的轴力,较大的轴力在风载波动的影响会致使绝缘子两端法兰松脱和固定松动。为了降低绝缘子轴力,提出了一种将绝缘子两端的不可移动约束转变为可移动的弹性约束支撑方式,以此降低绝缘子所受轴力,并通过仿真模拟验证了弹性支撑使用可以有效降低悬式绝缘子所受的轴力,大幅度提高了大挠度悬式绝缘子电流互感器在风载作用下的准确性稳定性和可靠性。
1 大挠度悬式绝缘子的风载计算
特高压直流电流互感器为了保证产品的绝缘性,一般采用悬式绝缘子进行绝缘,悬式绝缘子的长度会随着电压等级的升高而增长。当产品用于户外时,在风载和温度作用下悬式绝缘子会产生大变形,从而产生较大的支反力,因此研究大挠度绝缘子在风载作用下的受力特点,便于对特高压直流互感器悬式绝缘子的固定方式进行改进。
本次研究的大挠度绝缘子用于特高压直流电流互感器绝缘,其安装见图1,其主要包括传感头、绝缘子,花篮螺栓、挂箱以及均压环组成,其中绝缘子组件高压端吊耳法兰与传感头通过螺栓铰接,低压端光纤法兰与花篮通过螺栓铰接,其中大挠度悬式绝缘子的结构见图2,它由两端的固定法兰、环氧芯棒及硅橡胶伞裙组成。

图1 特高压直流电流互感器安装示意图Fig.1 UHV DC transformerinstallation diagram

1、4-金属法兰;2-环氧芯棒;3-硅橡胶伞裙
国内某工程的使用工况如下,环境温度:-34.8 ℃~36.7 ℃,最大日温差26 ℃,风速(离地面高10 m处,维持10 min的平均最大风速):29.7 m/s。因此风载的计算公式可以根据国标GB 50009-2012进行计算:
P=βzμsμzω0A
(1)
其中:βz为高度Z处的风振系数,取1.05(A类地区);μs为风荷载体型系数;μz为风压高度变化系数,取1.28(A类地区,离地面高度10 m);ω0为基本风压;A为绝缘子串的受风面积。
基本风压与风速的关系为
ω0=0.613v2
(2)
按10 min持续平均最大风速34 m/s核算:
ω0=0.709 kN/m2
悬式绝缘子可以视为圆筒状,外径为φ30,内径为φ18,则μzω0d1d2=0.000 8;取μs=1.2;其中涉及的受风面积可视为悬式绝缘子在风速方向上的投影,可以计算得出A=0.72 m2;由此计算出风载P:
P=1.05×1.2×1.28×709×0.72=823.3 N
2 大挠度悬式绝缘子在风载作用下的力学分析
根据特高压直流互感器的结构特点,绝缘子上下两端采用铰链连接,可以限制4个方向的自由度,根据悬式绝缘子两端的固定形式,可分为不可移动支撑和弹性支撑。当采用不可移动支撑时,绝缘子两个端点不会产生位移;当采用弹性支撑时,允许绝缘子两端可以在一定范围内进行移动,为了分析两种支撑特点,需要进行两种支撑条件下的力学分析。
2.1 不可移动支撑方式下大挠度悬式绝缘子在风载作用下的力学分析
当绝缘子采用不可以移动支撑时,两个端点不能产生3个轴向位移,绝缘子组件两端约束形式与风向有关,当风向与铰链的转动方向一致时,绝缘子两端约束视为平面铰链约束;当风向与铰链的转动方向垂直时,绝缘子两端约束视为固支约束。实际产品运行过程中在风向不确定的情况下,悬式绝缘子受力介于两端铰链约束和两端固支约束受力之间,因此研究绝缘子在这两种约束下的受力情况。
悬式绝缘子力学参数见表1,可以看出硅橡胶的弹性模量与抗拉强度远小于环氧芯棒,因此可以忽略硅胶强度对于后续分析的影响,可假定悬式绝缘子在风载作用下的主要承力部件为环氧芯棒,同时忽略重力对其影响,绝缘子在风载作用下的力学模型可简化为在特定边界条件下环氧芯棒在分布载荷作用下的力学问题。

表1 悬式绝缘子力学参数Table 1 Mechanical parameters of suspension insulator
假设在悬式绝缘子长度范围内风压变化较小,则悬式绝缘子所受到的风载可视为均布载荷,则两种约束下力学模型见图3。为了便于后续分析,将风载折算为线面度载荷进行计算,则:
(3)
由于绝缘子两端的固定点位置确定,在两种边界条件下,绝缘子两端均不产生位移,同时绝缘子属于细长杆结构,抗弯刚度较小,在风载作用下,弯曲变形较大,因此绝缘子会因为两端不可移动而产生轴力。轴力的产生使得绝缘子在风载作用下的弯曲转变为非线性的纵横弯曲。
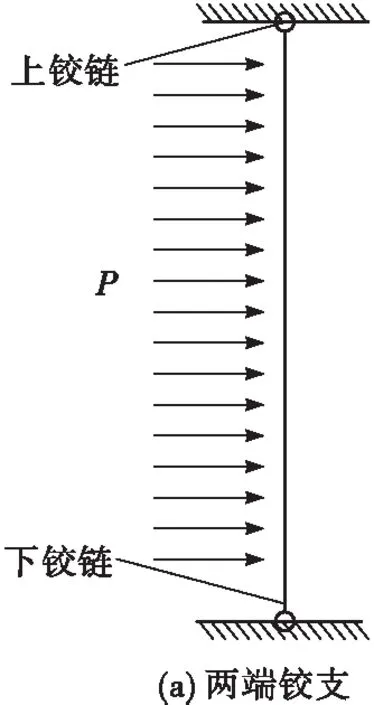
图3 风向与铰链转动方向相同与垂直时绝缘子力学模型示意图Fig.3 Schematic diagram of insulator mechanical model when the wind direction is the same as or perpendicular to the hinge rotation direction
为了便于计算,在风载作用下绝缘子挠曲线一般采用满足边界条件的曲线近似代替,对于两端铰支边界条件下的悬式绝缘子挠曲线函数这里取:
(4)
由于绝缘子长度较长,环氧芯棒抗弯刚度较小,在风载作用下弯曲程度较大,轴力不可忽略,轴力可由环氧芯棒沿轴线的伸长量进行计算,环氧芯棒沿轴线的伸长量ΔL可由下式计算[7-9]:

(5)
其中:
将被积函数根据泰勒展开,略去高阶无穷小,可得轴线伸长量:
(6)
联立(4)(6)得:
(7)
两端铰支时,绝缘子在风载作用下产生的轴力可由下式计算得出:
(8)
其中:S为环氧芯棒的截面积,s为绝缘子变形后挠曲线的弧长,f0为绝缘子中点处挠度,因此推导得出轴力为
(9)
由于绝缘子弯曲和轴向拉伸所具有的内力势能ΔU:

(10)
在环氧芯棒发生弯曲到稳定状态过程中,外力q产生的势能ΔV:
(11)
则总势能Π:
Π=ΔU+ΔV
(12)
由最小势能原理:
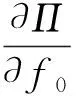
(13)
可知环氧芯棒在风载作用下的风摆量(中心弯曲挠度)为f0=0.15 m。
同理,假设两端固支约束悬式绝缘子的挠曲线方程为
(14)
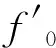
将风摆量f0带入式(5)可得绝缘子两端铰支时受到轴向力N0:
N0=7 900 N
N1=6 980 N
绝缘子两端固支时,在风载作用下绝缘子两端会产生弯矩,其值为
(15)
带入数据得:MA=MB=69.8 N·m
由上述分析结果可得,悬式绝缘子无论采用两端铰支,还是两端固支,由于绝缘子两端不能移动,会产生较大的轴力,而轴力过大会给绝缘子两端的固定带来困难。
2.2 不可移动支撑方式下悬式绝缘子在极限温度作用下受力分析
悬式绝缘子中的环氧芯棒主要以环氧树脂为基体材料,利用玻璃纤维增强树脂强度获得良好的使用性能。当温度变化时,环氧芯棒的长度会随之变化,使得环氧芯棒产生附加应力并影响绝缘子的形态,从而影响绝缘子力学性能。
考虑温度对环氧芯棒热胀冷缩的影响。玻璃纤维增强环氧树脂的线膨胀系数α=2.7×10-6/℃,在最大极限温差ΔT的条件下,环氧芯棒长度变化量l:
Δl=LαΔT=11.27×2.7×10-6×(36.7-(-34.8))
=0.002 175 m
由于环氧芯棒热变形量Δl产生的力FT:
当环氧芯棒长度变化量Δl是由于环氧芯棒冷缩引起时,环氧芯棒会由于两端约束限制其缩短而产生拉力,此时产生的FT为拉力。
当环氧芯棒长度变化量Δl是由于环氧芯棒热胀引起时,环氧芯棒会由于两端约束限制其膨胀而产生压力,此时产生的FT为压力。当压力FT超过其失稳时的临界压力时,绝缘子失稳,产生热屈曲[10-11],外在变现为绝缘子发生弯曲;当杆件发生失稳时,表现为弯曲变形量增大,压力恒定,为失稳时的临界压力。由于两端固支条件下临界压力大于两端铰支的临界压力,取两端铰支的临界压力做为绝缘子失稳的临界压力,其临界压力Fer为
因此环氧芯棒失稳,杆件弯曲,此时环氧芯棒所受的轴力为临界压力Fer=430 N。
采用非柔性的花篮螺栓,在风载作用下会产生7 910 N的拉力,在极限低温下因冷缩最大可产生3 494 N的拉力,同时由于绝缘子在风载作用下会产生振动,风载和温度产生的轴力在振动影响下会进一步放大,因此当风载和温度产生的轴力较大时,在拉力作用下容易造成悬式绝缘子中环氧芯棒与两端金属法兰分离及悬式绝缘子固定松动问题。为了解决此类问题,设计了柔性弹簧花篮螺栓,可以大幅度减少由于风载、温度及振动产生的拉力及波动幅值。
2.3 弹性支撑方式下大挠度悬式绝缘子在风载和温度作用下的力学分析
非柔性花篮螺栓的固定为不可移动的铰支固定,在风载和极限温度下会产生较大的轴力,因此其固定方式存在着一定的安全隐患。为了满足风载和温度工况,设计了可伸缩的弹性支撑方式,将固定支承转变成可移动支承,从而可以减小风载和极限温度引起的轴力,提高稳定性和可靠性。
弹性支撑解除了绝缘子下端的位移约束,允许悬式绝缘子下端具有一定的移动区间,因此可以消除在风载和热胀冷缩情况下绝缘子下端产生的轴力。
由上述计算结果可知,两端固定支撑,绝缘子在风载作用下轴向最大拉力N=7 900 N,对应的轴向移动量ΔLN为
在极限温度下悬式绝缘子因轴向收缩产生的拉力FT=3 494 N,对应轴向的缩短量LT为
通过弹簧实现弹性支撑,通过调节弹簧刚度和预紧力不同长度绝缘子的固定,施加给弹簧预紧力为F0=1 000 N,选用的弹簧长度为190 mm,弹性系数为33 N/mm,1 000 N预紧力对应的压缩量为30 mm,由于采用的弹簧刚度较小,当风载作用于绝缘子时,弹簧会被拉伸,当弹簧拉伸量为ΔLN时,绝缘子所受的轴力Fsq为
Fsq=kΔLN+F0=1 165 N
当芯棒产生低温收缩时,施加在绝缘子上的轴力FsT为
FsT=kΔLT+F0=1 072.6 N
同时由于预紧力的存在,弹簧花篮螺栓处于受拉状态,可以消除环氧芯棒的热屈曲效应,避免悬式绝缘子发生失稳,产生热弯曲。
3 悬式绝缘子两端不同支撑方式在风载作用下的有限元分析
在上述理论分析中,对风载作用下绝缘子挠曲线采用了满足边界条件的曲线近似代替,因此在计算过程会产生误差,为了核验计算误差,验证弹性支撑的实用性,对绝缘子在有无弹性支撑两种情况下对两种边界条件受力进行了有限元仿真。进而建立了不同刚度系数k、不同预紧力F0下的绝缘子仿真模型,探究了弹簧刚度和预紧力对悬式绝缘子的风摆量和力学参数的影响,为柔性弹簧花篮螺栓提供了设计依据。
3.1 两端铰支与两端固支不可移动支撑约束下绝缘子的有限元仿真模型
采用abaqus对悬式绝缘子进行有限元仿真。由于伞裙材料为硅橡胶,杨氏模量较小,在弯曲过程中可视为不抵抗弯曲变形,为了简化分析,仿真模型可作如下处理:忽略绝缘子重力和硅橡胶伞裙对抗弯的影响;假设风载为均布载荷;环氧芯棒作为唯一的抗弯部件。两种边界条件下的仿真结果见图4。

图4 两端铰支和两端固支有限元仿真结果Fig.4 The finite element simulation model result of flexible support and fixed support at both ends
对比理论分析结果和有限元仿真结果,悬式绝缘子在两端铰支和两端固支两种边界条件下由于风载产生的风摆量和支反力见表2。

表2 两端铰支、两端固支条件理论与有限元分析对比Table 2 Comparison betweenflexible support and fixed support at both ends
由表2可以看出:采用正弦和余弦曲线来假设绝缘子的挠曲线进行计算时,风摆量、轴力的理论计算结果与有限元仿真结果较为接近,最大误差分别为2.1%和1.5%;然而弯矩理论计算值与有限元仿真结果偏差很大。分析其原因为:为了简化计算,对两端固定约束下绝缘子的挠曲线采用前三阶余弦函数假设绝缘子两端固支挠曲线,此时整体位移误差很小,但是端部位移误差较大。由式(9) 和式(15)可知,轴力与整体的位移的平方成正比,因此可以准确描述;而弯矩与端部位移的二阶导数成正比,因此在端部会因为挠度误差较大产生较大的误差。
3.2 两端铰支与两端固支弹性支撑约束下绝缘子的有限元仿真模型
为了建立弹簧花篮螺栓在两种边界条件上有限元仿真模型,将弹簧等效为弹性杆,通过等效杨氏模量来进行分析。笔者设计的弹簧花篮螺栓长度为l=500 mm,刚度为k=33 N/mm,将弹簧等效为截面积与环氧芯棒相同的弹性杆,则弹性杆的等效杨氏模量ES:
(16)
因此通过等效的杨氏模量可以将弹簧等效为长度为l=500 mm,杨氏模量为ES=3.65×107Pa 的弹性杆,弹性杆与环氧芯棒的之间的约束关系,根据实际工况确定。弹簧花篮螺栓与风向的约束关系见图5,当风向与绝缘子转动轴垂直时,弹簧只能轴向拉伸,因此在有限元模型建立时,弹性杆的上端点只设置一个竖直方向的自由度;当风向与绝缘子转动轴平行时,弹性杆两端设置为铰链约束。初始预紧力可以通过设置弹簧下端的位移约束来实现,由于预紧力产生的弹簧位移为
(17)

图5 弹簧花篮螺栓与风向的约束关系示意图Fig.5 Schematic diagram of the constraint relationship between spring basket bolt and wind direction
为了探究弹簧刚度对于绝缘子风摆量,上端轴力与弯矩的影响,研究了5种工况,分别为刚度k=11 kN/mm,22 kN/mm,33 kN/mm,44 kN/mm,55 kN/mm,通过式(16)等效为Es=1.22×106Pa, 2.43×106Pa,3.65×106Pa,4.86×106Pa,6.1×106Pa。设置加载载荷q=73.1 N/m,预紧力F0=1 000 N。分别在两种边界条件下进行有限元仿真,风摆量,轴力和弯矩见表3。由表可以看出,随着弹簧刚度的增大,风摆量和上端弯矩不断减少,轴力不断增大。

表3 两端铰支、两端固支条件不同刚度对应的有限元分析结果Table 3 The finite element analysis result of flexible support and fixed support at both ends
为了探究预紧力F0对于风摆量,上端轴力与弯矩的影响,将弹簧刚度设置k=33 kN/mm。研究5种预紧力F0=500 N,750 N,1 000 N,1 250 N,1 500 N下力学参数的变化,预紧力F0通过式(17)等效为Δx0=15.2 mm,22.7 mm,30.3 mm,38.9 mm,45.45 mm的竖直向下的位移,并设置加载载荷q=73.1 N/m,分别在两种边界条件下进行有限元仿真,风摆量,轴力和弯矩见表4。由表可以看出,随着预紧力的增大,风摆量和上端弯矩不断减少,轴力不断增大。

表4 两端铰支、两端固支条件不同预紧力对应的有限元分析结果Table 4 The finite element analysis result of flexible support and fixed support at both ends
采用的弹性支撑弹簧的刚度系数为k=33 kN/mm,预紧力F0=1 000 N。根据仿真结果可知,绝缘子最大风摆量出现在两端铰支约束条件下,最大风摆量为458 mm,最大轴力为2 463 N。而采用两端固支和铰支时,风载作用下产生的轴向力为7 910 N。当考略风载和温度影响叠加时,未采用两端固支和铰支绝缘子因温度而产生的轴力增量为FT=3 494 N,因此总轴力为风载产生的轴力与热变形引起的轴力之和,数值为11 404 N,而采用弹性支撑时由于热变形弹簧产生的压力增量为kΔLT=72.6 N,总轴力为风载产生的轴力与弹簧产生的压力增量之和,数值为2 535.6 N,对比分析可以发现:采用弹簧支撑可以大大减小风载作用下产生的轴力。
同时由仿真结果可知:弹性支撑方式的使用在大幅度减小绝缘子受到轴力的同时,也会增大两端的弯矩和风摆量。由于绝缘子环氧芯棒与两端的金属法兰连接方式为压接,设计的最大抗拉载荷为Fd=10 kN。两端吊耳法兰承受的最大弯矩由抗弯试验可知M=1 157 N·m。对比仿真结果可以得出:在两端固支和铰支约束下,在温度和风载叠加情况下,绝缘子受到的轴力大于设计最大抗拉载荷。而采用弹簧支撑时在温度和风载叠加情况下,绝缘子受到的轴力远小于设计最大抗拉载荷,因此弹性支撑可以大幅度提高绝缘子的抗拉安全系数;虽然两端的弯矩稍有增加,最大弯矩为280 N·m,远小于实验给出的最大弯矩M=1 157 N·m,抗弯安全系数亦满足设计需求。因此本研究设计的弹性花篮螺栓,可以推广到户外绝缘子的安装工况中使用。
4 结论
根据上述分析可知,在风载作用下,悬式绝缘子会因轴向拉伸而产生轴向力,轴向力的大小直接影响悬式绝缘子的机械性能以及两端固支的可靠性,通过研究可知:
1)本研究提出的绝缘子弹性支撑,可以将悬式绝缘子的两端不可移动约束转换为可移动约束,通过计算分析可知:两端不可移动约束在风载作用下产生的轴力最大值为7 900 N,而采用弹性支撑绝缘子两端产生的轴力为2 463 N,极大的降低了在风载作用下轴力幅值。
2)采用弹性支撑可以有效的降低绝缘子由于冷缩产生的轴力以及热胀时由于热屈曲产生的弯曲失稳。
3)通过等效杨氏模量将弹簧等效为弹性杆,添加位移边界条件设置预紧力,建立的有限元模型,可以用于在弹性支撑约束下的绝缘子风载受力分析。
弹性支撑的使用,不仅可以有效的降低由于风载以及温度变化产生的轴向力幅值,而且可以有效地避免悬式绝缘子机械失效以及固定松脱的问题;同时也可以避免由于温升产生的热屈曲效应,因此本研究设计的弹性支撑方式具有工程使用价值。
