山区雷击高塔影响架空线感应过电压的模拟研究
2022-04-27张金波顾佳莹张其林
张金波, 顾佳莹, 张其林
(南京信息工程大学气象灾害教育部重点实验室/气候与环境变化国际合作联合实验室/气象灾害预报预警与评估协同创新中心/中国气象局气溶胶与云降水重点实验室, 南京 210044)
0 引 言
在电力系统中,雷电是引起架空配电线路电力故障的重要原因,尤其对110 kV以下的架空配电线路,因其架设高度低、分布范围广、绝缘相对薄弱等特点,雷电击中架空线路附近在线路上引起的感应过电压是威胁架空输配电线路安全稳定运行的主要原因[1]。因此,准确计算架空线上的雷电感应过电压,可为进一步研究架空线路的防雷工程设计与实施提供理论参考[2]。
针对架空线感应过电压的计算及其影响因素,国内外学者对此进行了大量研究,计算方法有解析法[3-4]与数值法[5-6],常用的传输线耦合模型主要有Agrawal模型[7]、Rachidi模型[8]和Taylor模型[9],线路感应过电压会受到土壤电导率及其分层结构[10-11]、土壤色散效应[12]、线路电晕效应[13]等因素的影响。实际情况中雷电更倾向于击中高塔等接地体,因此雷击高塔情况及其对架空线感应过电压的影响引起了学者的广泛关注,如Rachidi等[14],Rakov[15]提出雷击高塔模型,Baba和Rakov[16-17]利用FDTD算法计算发现雷击高塔时的感应过电压幅值明显高于雷击地面的情况,但以上研究仅考虑了平坦地面情况下的感应过电压特征。
近年来,不平坦地形对架空线感应过电压的影响受到重视,Soto等[18]利用2D-FDTD模型计算发现雷击山顶时山体坡度的增加也会使感应过电压幅值变大。张金波等[19]讨论了山体坡度及其电导率分层对感应过电压的影响,并在文献[20-21]中通过建立3D-FDTD算法模型,进一步讨论了雷击斜锥形复杂山体地形对架空线感应过电压的影响。考虑到在我国地势的多样性,部分地区的架空线通常架设于山区,山体地形在雷电感应过电压的准确计算中将是不可忽视的因素。
综上,为了综合讨论山区复杂地形条件下雷击高塔对架空线感应过电压的影响,笔者建立了3D-FDTD数值模型,利用共形网格技术模拟山体地形,考虑雷击高塔情况,并结合Agrawal耦合模型实现了对山区雷击高塔条件下雷电感应过电压的数值计算。此外,还以南京紫金山地形为例,给出了真实山体地形条件下雷击高塔影响感应过电压的一个算例。本研究内容有助于为山区架空输配电线路的防雷设计提供理论参考。
1 3D-FDTD模型介绍
本研究基于3D-FDTD算法建立模型,见图1,以典型的锥形山体地形为例,假设雷电击中山顶高塔,架空线路平行于山体坡面,其中,高塔的高度ht=100 m,山体坡度记为θ,山体底部宽度3 000 m,山体高度随坡度变化,例如,当θ=45°时,山体高度为1 500 m。其中架空线长L=1 000 m,离地高度h=10 m,线路半径a=5 mm,线路近端点距离回击通道d=100 m。三维模型的模拟空间长宽高分别为3 000 m、3 000 m、3 800 m,空间步长Δx=Δy=Δz=5 m,时间步长Δt=5 ns,满足Courant稳定性条件[22]。地面厚度为100 m,山体土壤的相对介电常数εr=10、电导率σg=0.001 S/m,空气的电参数为εr0=1、σ0=0 S/m,模型边界采用一阶Mur吸收边界[23]。
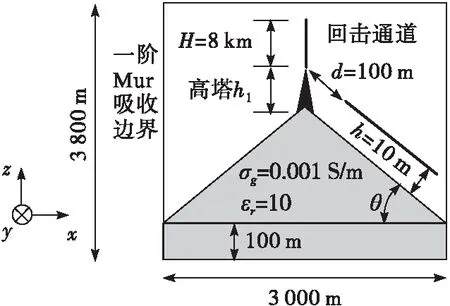
图1 三维FDTD计算模型示意图Fig.1 Configuration of 3-D FDTD simulation model
在本研究3D-FDTD模型中,对三维直角坐标系中的Ex、Ey、Ez和Hx、Hy、Hz这6个电磁场分量进行空间离散化,利用共形网格技术模拟复杂山区地形,在时域上迭代求解麦克斯韦方程组[22],然后,将计算得到的空间电磁场作为Agrawal场线耦合模型的激励源,进一步计算出架空线雷电感应过电压。
1.1 山区复杂地形的模拟
笔者在模拟复杂山体时,采用共形网格技术处理山体与空气两种介质分界面[24]。如图2(a)中同时包含2种介质的空间网格,对每一个离散的电场分量(Ex、Ey、Ez)定义各自的等效电参数[25]。图2(b)显示了山体介质中的各个电场分量在网格边长中所占长度分别是lx、ly、lz,则电场节点处的电参数的等效值可以由对应边上不同介质所占长度的加权平均求得。以等效电导率的计算为例:
(1)
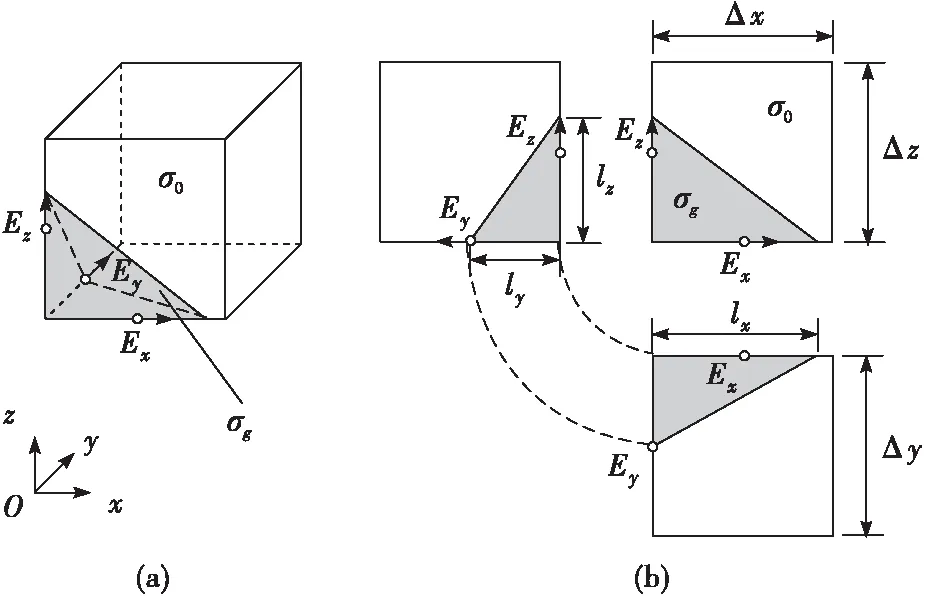
图2 3维FDTD共形网格技术Fig.2 Conformal 3D-FDTD techniques
1.2 雷电回击通道模型
假设雷电回击通道垂直击中山顶高塔,通道高度H=8 km,回击模型采用传输线(TL)模型[26],回击速度v取120 m/μs[18]。通道内的雷电流波形选择常用的双Heidler函数[27],即:
(2)
式中:i01和i02表示电流幅值;η1和η2分别是雷电流波形的上升沿和下降沿时间常数。选用继后回击电流参数[18]:i01=10.7 kA,τ11=0.95 μs,τ21=4.6 μs,i02=6.5 kA,τ12=4.7 μs,τ22=900 μs。
当雷电击中高塔时,见图3,由于雷电回击通道(Zch)、高塔(Zt)和大地(Zg)阻抗不匹配,导致雷电流在流经塔顶和塔底时将产生反射,塔顶(ρtop)和塔底(ρbot)的反射系数[16]分别为
(3)
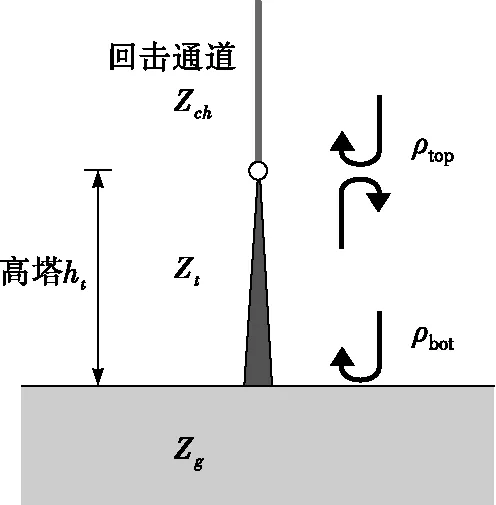
图3 雷击高塔模型Fig.3 Lightning strikes a tower model
采用Baba和Rakov[16]提出的雷击高塔模型,考虑雷电流在塔顶和塔底时产生的多次反射和叠加过程,雷电流在回击通道(ht (4) 式中:z表示离地高度,n=5表示电流反射次数,文中的反射系数[16]取典型值ρtop=-0.5,ρbot=1。 采用Agrawal耦合模型求解架空线上的雷电感应过电压[7]。根据Agrawal耦合模型,架空线的总感应过电压U(x)由入射电压Ui(x)和散射电压Us(x)组成,即U(x)=Us(x)+Ui(x)。其中Ui(x)是通过对垂直于架空线的电场分量Ep在高度h上的积分进行计算,而Us(x)是由时域的Agrawal耦合公式进行计算,表达式分别为 (5) (6) 式中:Ep和Et是沿架空线的垂直电场分量和切向电场分量;I是入射电流;L′和C′分别为理想传输线单位长度的分布电感和分布电容。线路两端保持阻抗匹配,接地阻抗RA和RB取值498 Ω。 采用FDTD方法对式(4)中感应电压和电流进行空间离散化,并进行迭代求解,空间步长和时间步长均与计算雷电电磁场的参数设置相同。值得注意的是,式(3)和(4)中沿架空线的Ep和Et与FDTD计算出的Ex和Ez位置和方向并不重合,需要进一步利用双线性插值法[21]计算Ep和Et,即根据线路节点附近的Ex和Ez分别在x方向和z方向进行线性插值,同时地形坡度,对架空线沿线分布的垂直电场分量Ep和切向电场分量Et进行计算。 与常用的2D-FDTD模型相比,3D-FDTD模型参数设置更灵活,便于模拟山区任意复杂地形,因此适用性更广,但算法更复杂,计算量也更大,本研究基于64位Windows系统Intel i7-6700 CPU计算平台,采用MATLAB软件进行编程和运算,完成一次运算超过36 h,占用内存约31 GB。为了验证3D-FDTD算法模型的有效性,首先将计算结果与文献[18]中的计算结果进行对比,此时锥形山体坡度分别为0°、26.6°、45°和63.4°,模型参数设置如上文所述,均与文献[18]保持一致。图4对比结果证实两者具有很好的一致性,这表明本研究在模拟山体地形条件下线路感应过电压的计算过程是准确的。 图4 本文结果与文献[18]结果的对比Fig.4 Comparison of our results with those from reference[18] 为了进一步验证本文雷击高塔算法模型的有效性,选取Baba和Rakov[17]文献中计算雷击100 m的高塔在架空线上产生的感应过电压作对比,如图5(a)给出的不同距离时架空线中点的感应过电压波形。模型参数与文献[17]一致,计算结果如图5(b)所示,对比结果表明两者基本一致,这证实了本研究雷击高塔模型的准确性。根据图4和图5的对比结果,可以证实3D-FDTD算法的有效性。 图5 本研究结果与文献[17]结果的对比Fig.5 Comparison of our results with those from reference [17] 首先考虑典型的锥形山体地形,并进一步考虑真实山区地形的模拟计算,综合考虑山区复杂地形和高塔的影响,模拟计算架空线上的感应过电压波形特征。 图6分别给出了锥形山体坡度θ=0°、26.6°、45°和63.4°时雷击高塔时的架空线两端的感应过电压,其中模型参数设置如上文所述,距离d=100 m,土壤电导率σg=0.001 S/m,当坡度θ=0°时,表示地形为理想平坦地面;当高塔高度ht=0 m时,表示不存在高塔。图6(a)表示线路近端点的感应过电压波形特征,可以发现,感应过电压明显随着地形坡度的增加而增大;当雷击山顶高塔时(即ht=100 m),感应过电压波形幅值进一步增大,波形产生了明显的波形震荡。图6(b)表示线路远端点的感应过电压波形特征,可以发现线路端点感应过电压极性与近端点感应过电压相反,这与文献[20-21]中的计算结果是一致的。其变化趋势与近端点过电压类似,随着地形坡度的增加,过电压幅值也随之增大,当存在高塔时,远端点感应过电压波形同样产生了明显震荡,产生幅值也显著增大。 图6 架空线路感应过电压波形Fig.6 Induced voltages of overhead lines 图7进一步统计了架空线端点感应过电压幅值的变化趋势,可以直观的看出,线路两端的感应过电压极性相反,但均随着地形坡度的增加而增大。对于近端点感应过电压,当不存在高塔时(即ht=0 m),其幅值随着地形坡度的增加而增大,例如,与平坦地形情况(即θ=0°)相比,坡度θ=26.6°、45°、63.4°时的近端点感应过电压幅值分别增大了40.3%、62.2%、283.0%;当考虑雷击高塔时(即ht=100 m),幅值进一步增大,以坡度θ=45°时地形为例,雷击山顶高塔时的近端点感应过电压幅值比雷电直击山顶时增大了16.5%。对于远端点感应过电压,当不存在高塔时(即ht=0 m),与平坦地形情况(即θ=0°)相比,坡度θ=26.6°、45°、63.4°时的远端点感应过电压幅值分别增大了71.4%、111.4%、367.8%;考虑雷击雷击高塔时(即ht=100 m),同样以坡度θ=45°时地形为例,雷击山顶高塔时的远端点感应过电压负峰值比雷电直击山顶时增大了73.5%,远端点感应过电压增幅大于近端点。 图7 不同坡度对应的架空线路感应过电压幅值Fig.7 Peak values of induced voltages of overhead lines for different slopes 除了山体地形坡度会对雷击山顶高塔时的架空线感应过电压产生影响,笔者进一步计算了距离、塔高、土壤电导率的影响。图8给出了线路近端点距离回击通道d=100 m、200 m和300 m时的架空线路感应过电压,此时山体坡度θ=45°、塔高ht=100 m、土壤电导率σg=0.001 S/m保持不变,对比结果显示,架空线两端的感应过电压幅值随着距离的增加而减小这主要是因为雷击电磁场会随着距离的增加而衰减。 图8 不同距离对应的架空线路感应过电压Fig.8 Induced voltages of overhead lines for different distances 图9给出了不同高度的高塔(ht=50 m、100 m、150 m)对线路感应过电压的影响,其中线路距离d=100 m、山体坡度θ=45°、土壤电导率σg=0.001 S/m保持不变,结果表明,随着塔高的增加,架空线两端的感应过电压幅值变大,波形震荡也更加明显。 图9 不同塔高对应的架空线路感应过电压Fig.9 Induced voltages of overhead lines for different tower heights 图10给出了不同土壤电导率(σg=0.1 S/m、0.01 S/m、0.001 S/m)对线路感应过电压的影响,其中线路距离d=100 m、山体坡度θ=45°、塔高ht=100 m保持不变,结果表明,架空线两端的感应过电压幅值随电导率的降低而变大。 图10 不同土壤电导率对应的架空线路感应过电压Fig.10 Induced voltages of overhead lines for different soil conductivities 上文讨论了典型的锥形山体地形情况,实际情况中的山区地形往往复杂多样,笔者以南京紫金山地形为例,进一步计算了真实地形条件下雷击山顶高塔时的线路雷电感应过电压。图11(a)是3D-FDTD模式中所导入的紫金山地区的数值高程模型(Digital Elevation Model,DEM)地形数据,N表示实际地理朝北方向。图11(b)是模型的剖面图,其中土壤电导率为0.001 S/m,雷电垂直击中山顶高塔,架空线沿山坡分布,线长1 000 m,离地高度10 m,近端点距离雷电通道100 m,其余参数的设置均与上文一致。 图11 真实山体地形(以南京紫金山为例)Fig.11 Real mountainous terrain (Purple Mountain in Nanjing) 图12分布给出了线路两端的感应过电压波形对比结果,可以发现,线路感应过电压幅值在雷击理想平坦地面时最小,雷击山顶时次之,雷击山顶高塔时最大。与理想平坦地面的情况相比,线路近端点感应过电压幅值在雷击山顶高塔、雷击山顶时分别增大了43.5%、50.2%,线路远端点感应过电压幅值在雷击山顶高塔、雷击山顶时分别增大了48.9%、124.3%。这意味着在山区架空输配电线路的防雷设计中,除了要考虑地形的影响,高塔也是不可忽略的影响因素。 图12 真实山体地形下架空线路感应过电压波形Fig.12 Induced voltages of overhead lines over real mountainous terrain 本研究建立了3D-FDTD数值模型,实现了复杂地形条件下雷击高塔对架空线感应过电压的计算,得到以下结论: 1)与雷击平坦地面相比,架空线两端的感应过电压幅值随锥形山体坡度的增加而增大,且坡度越大,增幅越大。 2)当雷击山顶高塔时,线路两端的感应过电压幅值随着距离的增加而减小、随塔高的增加而增大、随电导率的降低而增大。与雷击山顶相比,雷击山顶高塔时线路两端的感应过电压波形产生了明显震荡,波形幅值进一步增大。 3)文中给出了真实山区地形条件下(以南京紫金山为例)雷击高塔时的感应过电压。模拟结果发现与雷击平坦地面相比,雷击山顶时的线路两端过电压幅值分别提高了43.5%和48.9%,雷击山顶高塔时的线路两端过电压幅值分别提高了50.2%和124.3%。1.3 Agrawal场线耦合模型
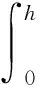
2 算法有效性验证
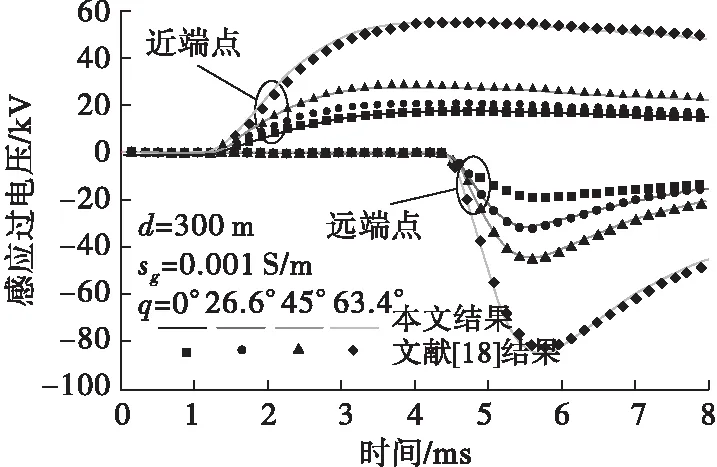
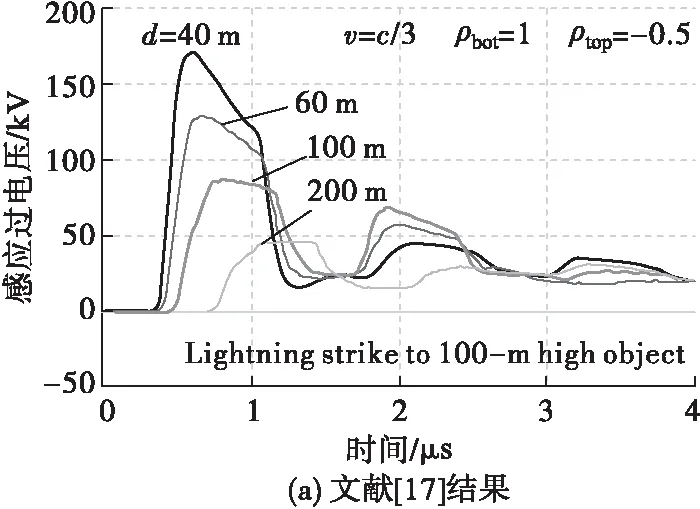
3 模拟结果分析
3.1 锥形山体地形情况
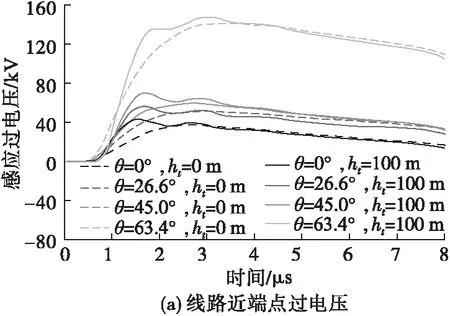

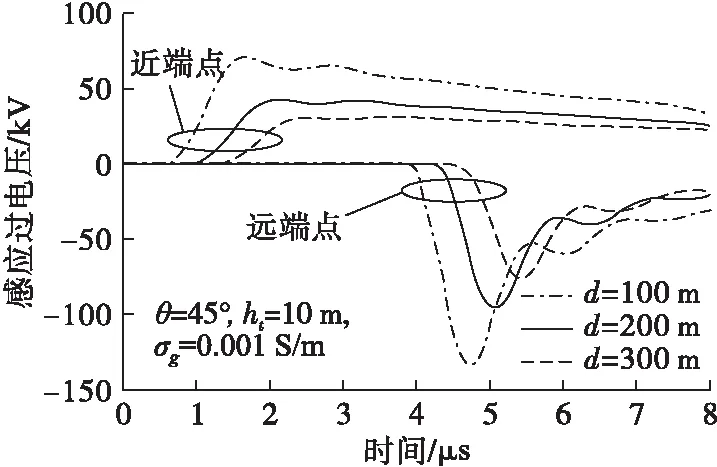

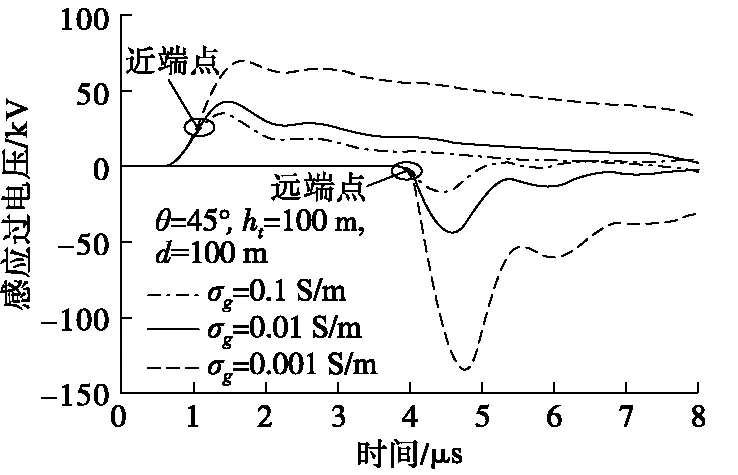
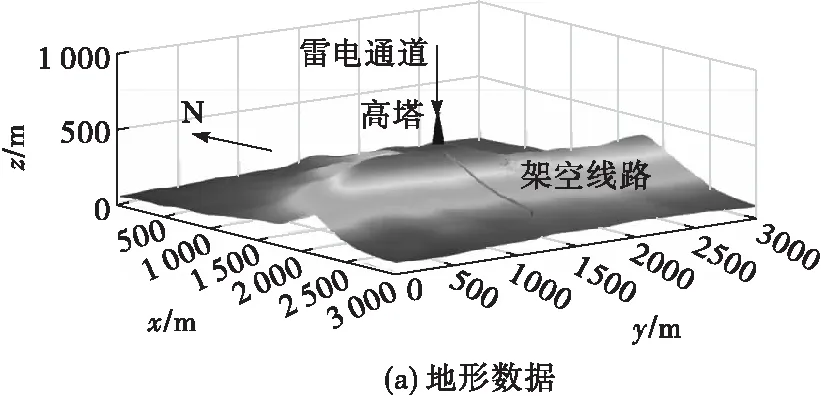
3.2 真实山体地形(以紫金山为例)情况
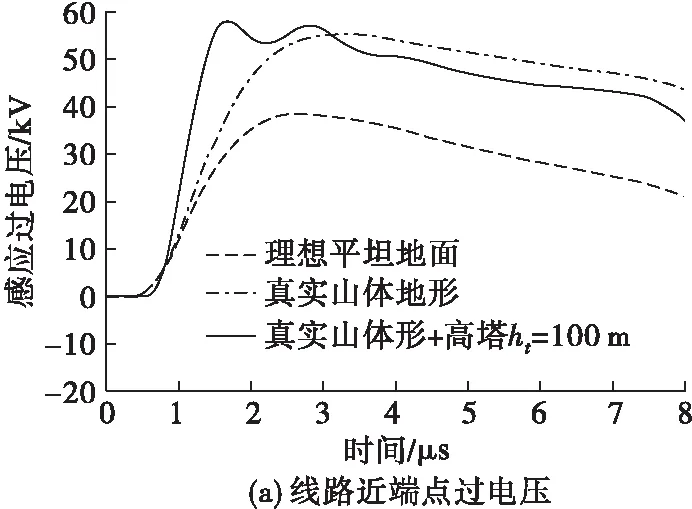
4 结 论
