某前悬架下摆臂疲劳失效分析与优化

2022-04-27梁国栋

机械设计与制造 2022年3期

梁国栋，程乐

（1.河源职业技术学院机电工程学院，广东河源 517000；2.淮安信息职业技术学院计算机与通信工程学院，江苏淮安 223003）

1 引言

悬架系统作为车辆的关键部件，其主要作用是传递载荷激励，并且减缓车辆在行驶过程中路面对车身的冲击和振动，以此能够提升车辆的稳定性和舒适性。下摆臂作为乘用车前悬架系统重要的导向和传力部件，其前端和后端均与前副车架相连，其外端与转向节相连，其强度特性与疲劳特性影响整车性能的稳定与安全。

某汽车前悬架下摆臂在进行整车道路耐久试验（目标要求试验里程60000km）时出现开裂失效问题，截止下摆臂开裂失效时共计试验里程数为32316km，其开裂起始位置位于上板与下板外侧边缘连接处，如图1所示。通过宏观判断可知，下摆臂开裂起始位置的裂纹较深，有明显裂纹扩展现象，因此其可能由疲劳引起的失效。

图1 下摆臂开裂位置Fig.1 Crack Position of Lower Arm

文献［1］为了解决某后悬架拖曳臂失效问题，建立悬挂系统有限元模型，对拖曳臂进行强度分析和试验对标分析，通过在其螺栓孔处焊接垫片，改进之后的疲劳和强度性能明显提升，并且通过了台架验证。文献［2］基于Hypermesh软件建立某控制臂有限元模型，并建立刚柔耦合悬架模型，提取其典型工况的载荷，基于惯性释放法对其进行强度校核分析，其应力均小于其许用应力，满足设计要求。文献［3］针对某前悬摆臂开裂问题，采用有限元法对其进行强度分析，其应力集中置与开裂位置相符，改进之后的摆臂通过了台架耐久试验验证。文献［4］为了解决某双叉臂悬架上摆臂开裂问题，对其进行有限元强度分析、疲劳分析和台架试验，基于集成平台对其进行优化设计，优化之后其通过台架试验和整车试验。

为解决该前悬架下摆臂疲劳失效问题，综合以上分析方法，首先采用有限元方法建立下摆臂模型，并建立前悬架动力学模型提前其极限工况的载荷，对其进行强度分析，然后进行台架试验对标分析，然后进行疲劳寿命预测分析和优化设计，最后进行台架和道路耐久验证。

2 下摆臂极限强度分析

2.1 建立下摆臂有限元模型

该前悬架下摆臂主要由上板、下板、轴管、衬管和球销等组成，上板厚度为3.0mm，下板厚度为3.0mm，下摆臂重量为3.1kg，上板和下板的材料为QSTE420TM，其屈服强度为420MPa，将下摆臂三维模型导入Hypermesh软件中。上板、下板、轴管和衬管属于薄钣金结构，对其进行抽中面处理，采用4mm的四节点单元对其中性面进行网格划分。球销属于铸件结构，对其进行表面几何清理，采用4mm的三节点单元对其表面进行网格划分，并且生成四面体单元。上板、下板、轴管和衬管之间的焊接采用垂直对齐的四节点单元模拟，球销与上、下板之间的螺栓采用刚性单元模拟，建立该前悬架下摆臂有限元模型，如图2所示。

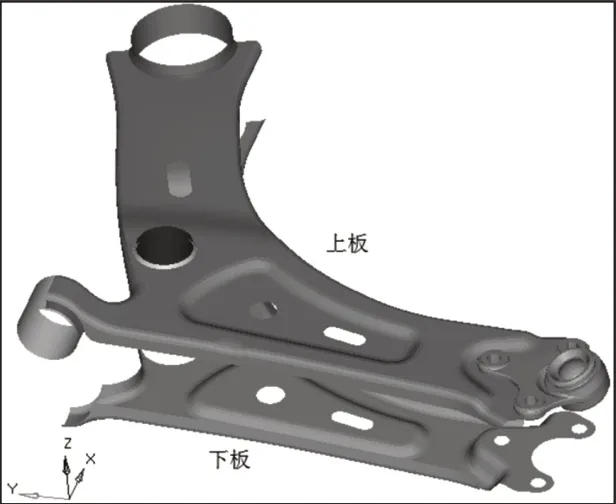
图2 下摆臂有限元模型Fig.2 Finite Element Model of Lower Arm

2.2 建立前悬架动力学模型

前悬架系统主要由前副车架、下摆臂和横向稳定杆组成，下摆臂在车辆行驶过程中，其最恶劣工况通常发生在车辆制动时，主要来自纵向载荷，因此基于整车参数并且采用Adams∕Car软件［5］建立前悬架动力学模型。基于制动工况时轮胎接地点的受力状态对其进行静态求解，得到下摆臂前端、后端和外端的载荷。

2.3 强度分析结果

根据下摆臂有限元模型和前悬架动力学模型提取的极限工况载荷并采用惯性释放方法对其进行极限强度分析，获取其极限强度性能。下摆臂应力云图，如图3所示。由图3可知，下摆臂在极限制动工况时的最大应力为412.2MPa，接近于其材料屈服极限，存在疲劳失效风险，并且其应力集中点位置与实际开裂位置一致。

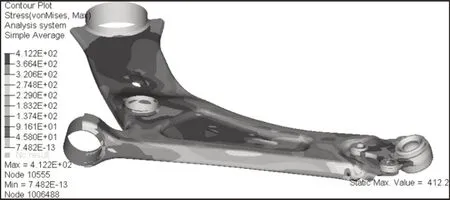
图3 下摆臂应力云图Fig.3 Stress Nephogram of Lower Arm

3 下摆臂台架试验对标

3.1 台架试验

为了校核下摆臂极限强度分析的准确度，在下摆臂开裂失效位置布置一个应变花传感器，并且定义其三个方向0°、45°和90°。为了准确获取下摆臂的应力，应该搭建前悬架系统台架，主要包括白车身、前副车架、减震器、转向节和轮毂等，采用固定装置约束白车身的所有自由度，采用吊钩使轮毂处于实际装车状态，采用液压缸在轮毂中心处以正弦方式施加纵向载荷6370N，模拟车辆极限制动工况，如图4所示。

图4 下摆臂台架试验Fig.4 Bench Test of Lower Arm

3.2 对标分析结果

如图5所示，为下摆臂应变花在0°、45°和90°的测试数据，采用nCode-DesignLife软件将其转换为相应的应力数据，下摆臂测试位置的最大应力水平为414.0MPa，其仿真值的误差率4.3%，具有比较高的准确性与可行性。

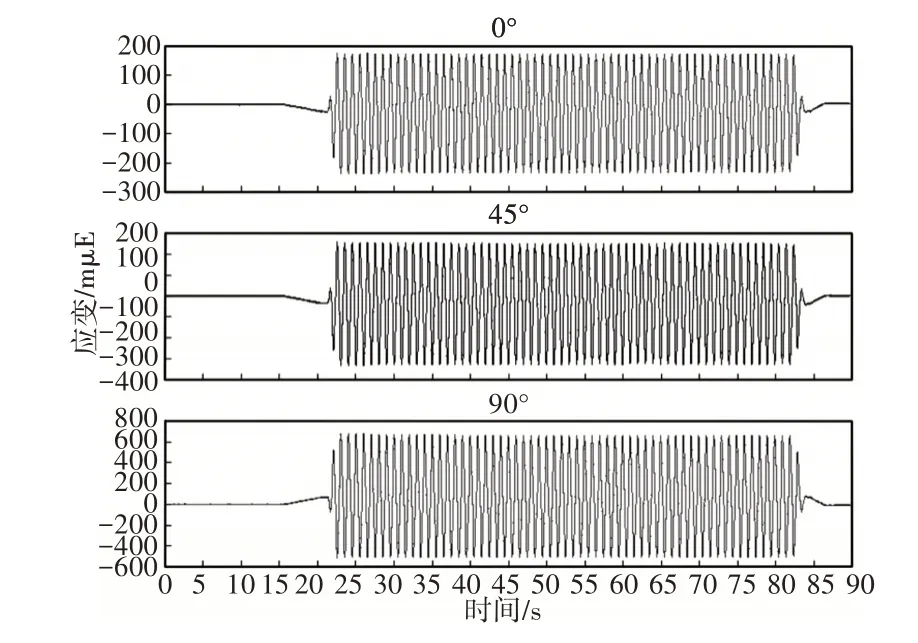
图5 下摆臂应变测试数据Fig.5 Strain Test Data of Lower Arm

4 下摆臂疲劳寿命分析

4.1 疲劳寿命分析基础

Miner疲劳线性损伤累积法则［6］是指结构在各级载荷下的损伤值是相互独立的，结构的总损伤值是线性累积的，若其损伤值累积至某一临界值时，结构将会发生破坏失效，即：

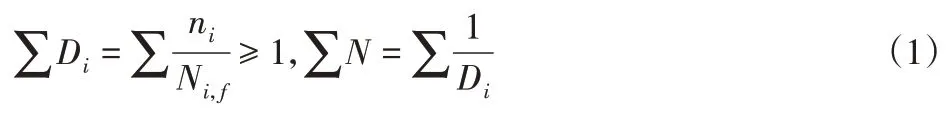
式中：D i—结构在各级载荷作用下对应的疲劳损伤值；

n i—结构在各级载荷作用下对应的疲劳循环次数；

N i，f—结构在各级载荷作用下的疲劳极限次数；

∑N—结构的总疲劳寿命。

4.2 疲劳分析结果

为了准确得到下摆臂的疲劳寿命，基于极限强度载荷并且采用nCode-DesignLife软件以正弦波加载，辅以自动合成的QSTE-420TM的S-N曲线对其进行疲劳寿命分析。下摆臂疲劳寿命云图，如图6所示。

图6 下摆臂疲劳寿命云图Fig.6 Fatigue Life Nephogram of Lower Arm

由图6可知，下摆臂的最低疲劳循环次数为4.54E+4次，小于实际工程目标要求值（1.0E+5），不满足疲劳设计要求，并且其薄弱位置也与失效位置相同，因此该疲劳分析方法具有较高的可靠度。

5 下摆臂优化设计

5.1 优化设计模型

为了提升下摆臂的疲劳强度性能，因尽量降低开裂失效位置的应力集中现象，增加其该处的刚度，因此将下摆臂的上板厚度和下板厚度作为设计变量，将下摆臂的最大应力水平最小化和疲劳寿命最大化作为目标函数，同时尽量减轻其重量，建立优化设计模型：

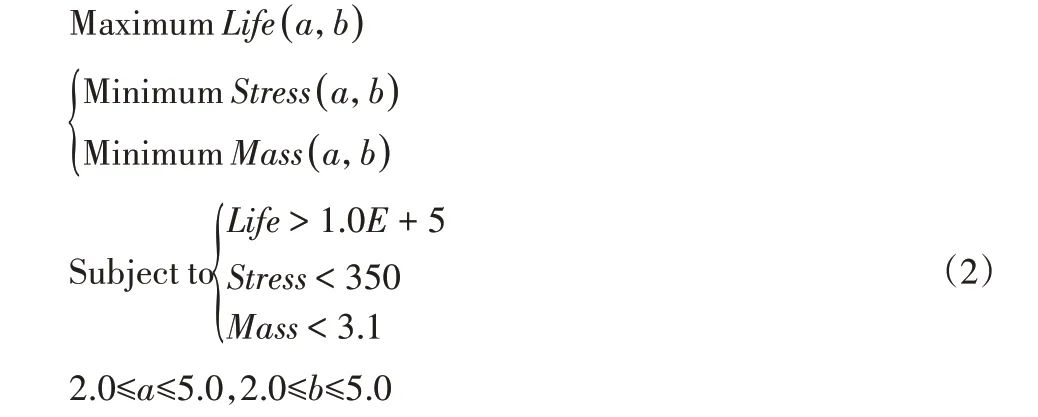
式中：Life—下摆臂的疲劳寿命；

Stress—下摆臂的最大应力水平；

Mass—下摆臂的重量；

a—下摆臂上板的厚度；

b—下摆臂下板的厚度。

5.2 优化设计结果

采用Isight平台［7］集成下摆臂有限元模型、极限强度分析和疲劳寿命分析，根据优化模型设置相应的目标函数、设计变量及其范围，基于多目标梯度探索算法对其进行优化分析。Isight集成平台经过86次迭代计算最终达到收敛，得到下摆臂厚度的最优解。优化前后的下摆臂厚度，如表1所示。由表1可知，优化之后下摆臂上板的最佳厚度为3.3mm，下板的最佳厚度为2.5mm。

表1 优化前后的下摆臂厚度Tab.1 Lower Arm Thickness Before and After Optimization

基于下摆臂厚度的最优值，采用相同的方法对其进行极限强度分析，得到优化之后下摆臂的最大应力为347.8MPa，与优化之前相比，其应力降低15.6%，其安全系数达到1.21，并且其应力集中点转移到下板内侧，不易发生失效风险，符合强度特性要求。

基于下摆臂厚度的最优值，采用相同的方法对其进行疲劳寿命预测分析，得到优化之后的下摆臂疲劳寿命云图，如图7所示。由图7可知，优化之后下摆臂的最低疲劳循环次数为1.25E+5，高于实际工程目标值，与优化之前相比，其疲劳性能提高了1.75倍，并且其薄弱点也转移到下板内侧，符合疲劳设计要求。

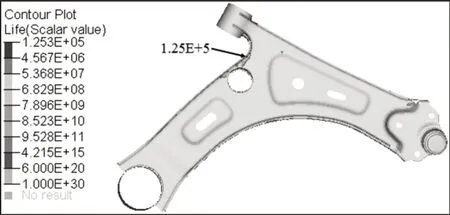
图7 优化之后的下摆臂疲劳寿命云图Fig.7 Fatigue Life Nephogram of Lower Arm after Optimization

基于下摆臂厚度的最优值重新计算，得到优化之后下摆臂的重量。如表2所示，为优化前后的目标函数，由表2可知，优化之后下摆臂的重量为2.9kg，与优化之前相比，其减轻了6.5%。优化之后的下摆臂强度性能和疲劳性能均可以满足设计要求，并且达到了轻量化的目的，优化效果比较理想。

表2 优化前后的目标函数Tab.2 Objective Function Before and After Optimization

6 优化方案验证

为了对该下摆臂优化方案的可靠度进行验证，根据最佳设计参数制作下摆臂优化方案样件，如图12所示。基于下摆臂台架试验平台采用液压缸在轮毂中心处以正弦方式施加纵向载荷6370N，对其进行台架验证。台架试验在进行1.5E+5次后发生开裂，其疲劳仿真值的精度达到了83.3%，并且其开裂位置与疲劳寿命分析的薄弱位置一致。

图8 下摆臂优化方案样件Fig.8 Prototype of Lower Arm Optimization scheme

与此同时，为了验证下摆臂优化方案载整车状态下的稳定性，将其装配在试验车上。基于整车道路耐久试验标准，分别在高速路、扭曲路、比利时路、凸块路、长波路、短波路和搓板路进行整车验证，道路试验总里程为60000km，整个试验过程下摆臂没有发生异响，试验完成后下摆臂也没有发生开裂失效问题，因此该下摆臂优化方案具有较高的可行性。