机械臂系统鲁棒控制轨迹跟踪

余 涛，甄圣超，陈小龙

（合肥工业大学机械工程学院，安徽 合肥 230009）

1 引言

近年来，机械臂在工业自动化生产中得到了广泛的应用，很多应用场合如打磨、焊接、装配等要求机械臂能够精确跟踪轨迹运动，具有不确定性的机械臂系统轨迹跟踪控制一直是控制领域的研究热点[1-2]。

目前，针对不确定性机械臂系统的控制方法主要有自适应控制和鲁棒控制，自适应控制可以不断学习、辨识不确定性参数调整自适应律，但是无法应用于具有结构不确定性的系统，且要求控制系统具备很高的实时计算能力；鲁棒控制具有固定的控制结构，它能够补偿系统中结构性不确定性和非结构性不确定性，如抑制外界干扰和补偿未建模动态不确定性，并且易于实现。目前，鲁棒控制器的设计方法主要是基于H∞、μ、Kharitonov、Lyapunov、QFT五种理论，前三种主要用于线性时不变系统，QFT虽然在实际应用中适用于非线性系统，但其理论基础尚需进一步论证，Lyapunov方法是迄今为止唯一建立了理论基础并适用于非自治非线性系统的方法[3-4]。

基于Udwadia-Kalaba方程的机械系统动力学控制方法在各个领域受到广泛的应用[5-7]，该方法特点是将机械系统的轨迹要求看作一种约束，再结合系统的无约束动力学模型，可以在不引入拉格朗日乘子的条件下对约束力进行求解。但是该方法在应用过程中必须初始条件相容且依赖于系统的精确动力学模型，而且机械臂系统是一个多输入、多输出、强耦合的复杂非线性系统，建模过程中存在参数测量误差、外界扰动、负载变化和未建模动态等不确定性因素影响，因此很难建立精确的机械臂系统的精确动力学模型[8-10]。

针对Udwadia-Kalaba方法难以解决机械臂系统不确定性问题和要求初始条件相容的问题，设计了一种新的鲁棒控制算法，并且基于Lyapunov理论证明了该控制算法具有一致有界性和一致最终有界性，仿真试验结果表明所提控制方法的有效性和鲁棒性，能够控制臂沿着期望的轨迹精确运动。

2 问题描述

机械臂系统的动力学模型一般方程如下：

由于测量误差、外界干扰以及负载不确定性的影响，（1）式中的矩阵可以被拆解为精确值标称部分和不确定性部分。

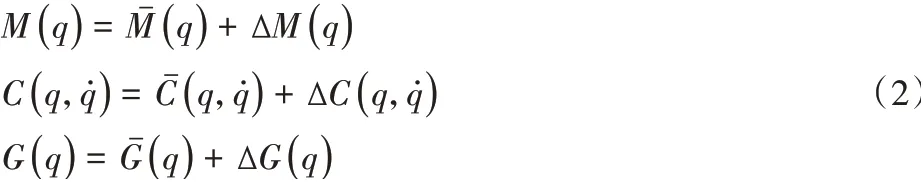
基于Udwadia-Kalaba方程的动力学控制过程如下：

（1）求得机械系统的无约束动力学方程；

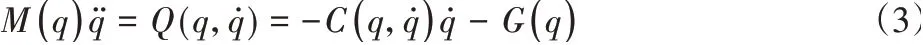
（2）将给定的轨迹约束写成二阶微分形式；

（3）得到机械系统在轨迹约束下的约束力；

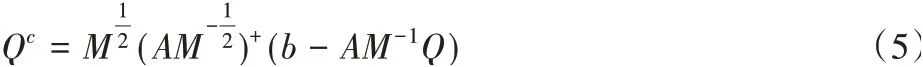
式中：Qc—系统约束力广义逆矩阵。

根据以上分析，基于Udwadia-Kalaba方程控制要求得到机械臂系统的精确动力学模型，这在实际情况下是不可能的。实际机械臂系统总是存在各种不确定性，如参数时变、负载变化、以及未建模动态等，这些不确定性因素导致Udwadia-Kalaba方程控制难以保证系统的控制精度和稳定性。为了抑制不确定因素的影响，在Udwadia-Kalaba方程控制基础上设计一个鲁棒控制器对于不确定性机械臂系统是很有必要的。

3 鲁棒控制器的设计

基于Udwadia-Kalaba方程，提出如下鲁棒控制器：

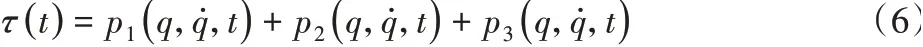
其中，

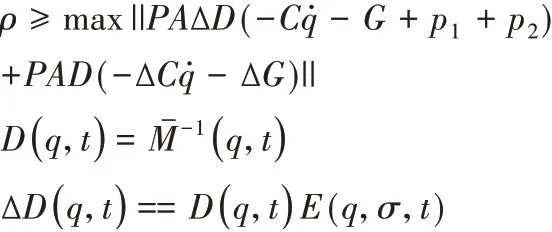
稳定性分析：

选取李雅普诺夫函数为：

对上式进行求导得：

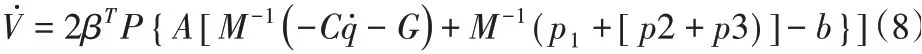
根据p1值得，

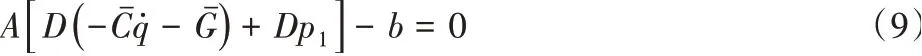
根据p2值得，

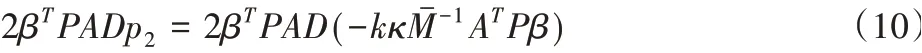
根据p3值得，

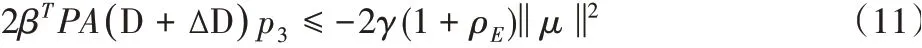
最终，我们可以得到，

基于上面的分析，证明控制器满足一致有界性和一致最终有界性［11］，表明系统是稳定的。

4 仿真结果与分析

平面二自由度机械臂示意图，如图1所示。假设连杆为均质杆，连杆1和连杆2长度为l1和l2，质量为m1和m2；关节1与关节2的相对转角为θ1和θ2，关节1与关节2的力矩分别为τ1和τ2。关节2处的电机质量为m3，夹取物件的质量为m4，重力加速度为g。

图1 二自由度机械臂模型Fig.1 Two-Degree-of-Freedom Manipulator Model

根据拉格朗日建模可以推导出该系统的动力学方程，

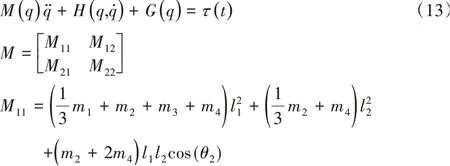
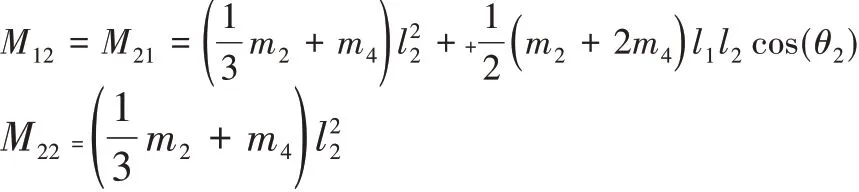
选取仿真时期望轨迹：

上式对时间求二阶导数，可得到二阶约束形式：

写成矩阵形式：

仿真结果图，如图2～图6所示，可以看出，在约束轨迹初始条件不相容时，在设计的鲁棒控制算法作用下，机械臂关节1和关节2的角度偏差能够快速趋近于零，说明机械臂系统能够快速跟踪期望约束轨迹。表明所提控制算法可以解决机械臂系统初始条件不相容问题和系统不确定性问题。

图2 关节1角度变化曲线Fig.2 Angle Curve of Joint One

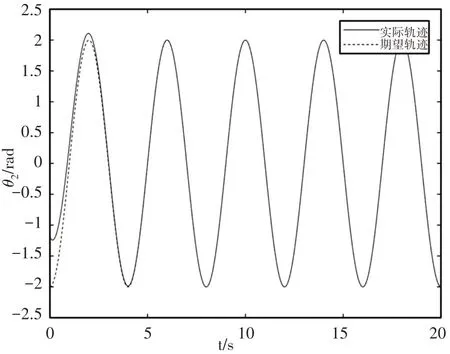
图3 关节2角度变化曲线Fig.3 Angle Curve of Joint Two

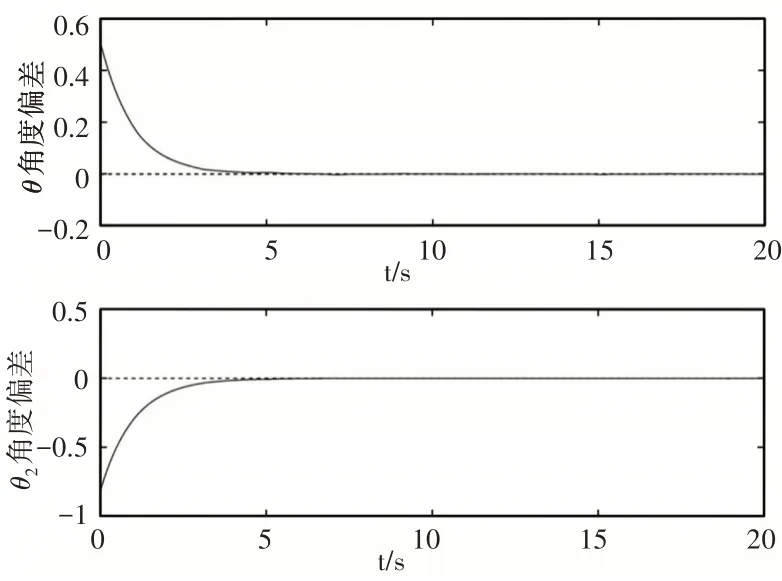
图4 关节1和关节2的角度偏差曲线Fig.4 Angle Curve of Joint One and Joint Two

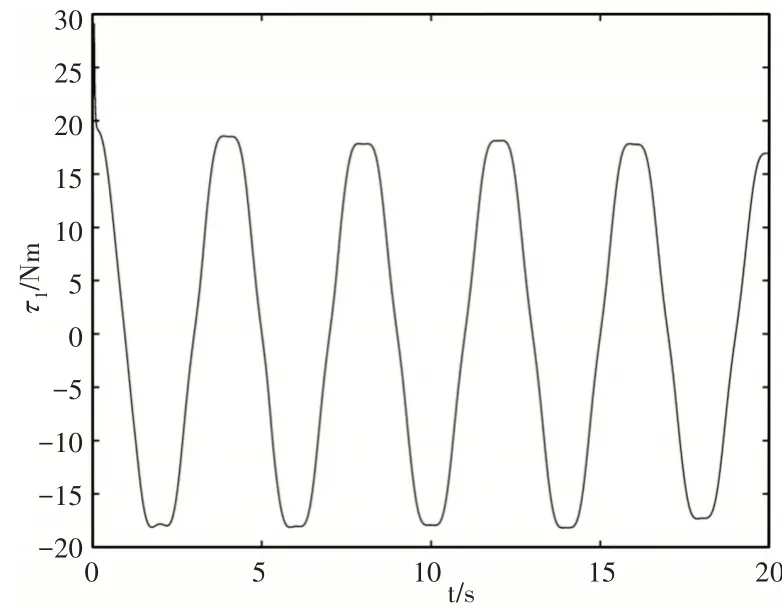
图5 关节1控制力矩Fig.5 Control Torque of Joint One

图6 关节2控制力矩Fig.6 Control Torque of Joint Two

5 结论

针对具有不确定性的机械臂系统轨迹跟踪控制问题，基于Udwadia-Kalaba方程设计了一种新的鲁棒控制算法。该控制算法能够有效解决机械臂系统不确定性问题和初始条件不相容的问题，为了验证控制方法的有效性和鲁棒性，针对平面二自由度机械臂系统进行了仿真试验。仿真结果表明：在轨迹初始条件不相容的情况下，该控制算法能够克服系统不确定性的影响，控制机械臂跟踪期望轨迹精确运动。