Stewart型六自由度并联运动平台运动分析及仿真

李海涛，马 军

（陕西科技大学机电工程学院，陕西 西安 710021）

1 引言

并联机器人，与串联机器人相比，具有闭链约束是并联机器人在结构方面最大特点，不仅抵消了误差累积效应，且运动惯量低、负载能力强、刚度大，使并联机器人成为潜在的高速度、高精度运动平台。六自由度平台实物[1]，如图1所示。其结构，如图2所示

图1 六自由度机械平台实物图Fig.1 Physical Drawing of 6-DOF Mechanical Platform

图2 机械平台结构图Fig.2 Structural Drawing of Mechanical Platform

六自由度并联运动平台的空间解析正解的求解一直是一大难点，至今仍不完善。当下，并联机器人正解常用解析法和数值法。文献[2]只是对正解方法和现状及原因做了简单的描述；文献[3-8]等提出的求解方法存在适用性差、计算复杂、效率低、仿真模型不完整等缺点。文献[9]采用双链交叉算子的遗传算法较精确地控制并联机器人，但其实时性不强，不能达到快速准确的效果；文献[10]采用粒子群算法求解正解，但较复杂，很难快速得到结果。

六自由度并联机器人运动仿真，很多研究人员用的是AD‐MAS、Solidworks、UG等[11]，但有建模复杂、运动参数调整不灵活等缺点。其次，MATALB自带的Stewart仿真模型内部系统设计复杂，运算有延迟。

鉴于此，采用隐函数图解法编写MATALB程序，进而快速解算平台的运动学正解，能在1s内解算出结果，并且对比计算误差仅在0.05%内。又通过建立MATLAB∕SimMechanics模型进行实例模拟，结果与预设轨迹基本吻合，进一步验证了方法的正确性与可靠性，同时有助于对运动平台实时控制。

2 运动学建模与求解

六自由度并联机器人的运动学分析包含坐标变换及位姿正反解。

2.1 移动坐标变换

高度不变时，上平台从初始位置沿直线向任意方向平行移动到某一个位置时六根支杆的长度随位移变化的情况。

设分别沿X、Y、Z轴平移r、q、s，则平移后

2.1.1 高度不变，已知移动的中心点求杆长—反解

（1）建系：以固定平台的中心为原点，所在面为X O Y面，由右手定则Z轴向上。设定两个距离近的万向节之间的夹角为θA，下固定平台的半径为R，上平台的半径为r。

（2）固定平台的6个坐标点空间坐标分别为：

（3）假定平台高度为h，为便于建系，设定上下平台连接的两个万向节夹角为30°，用AutoCAD画出上下平台俯视图，如图3所示。对于上面的平台的6个坐标点的空间坐标分别为：

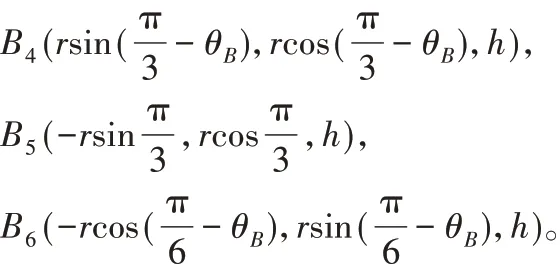
图3 上下平台俯视图Fig.3 Top View of Upper and Lower Platform

（4）当h不变及下平台固定（下平台固定中心坐标为O A(0，0，0)，上平台原中心坐标为O B(0，0，h)）时，上平台水平向任意方向移动，如图4所示。假设移至空间坐标点O1(x0，y0，h)，则方 向 向 量已 知，且 移 动 距 离 为已 知 ，则且平移方向的夹角为

图4 平台移动图Fig.4 Platform Mobility

对于B1点，设B'1(x1，y1，h)，则x1=0+Ssinϕ，y1=-r+Scosϕ，h不变。故，

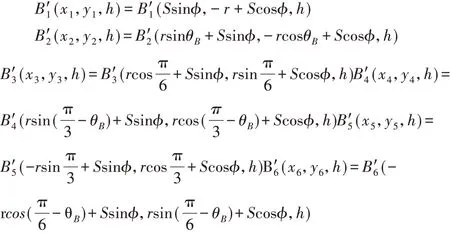
（6）为避免公式推算繁琐，利用MATLAB编程对实例进行数值求解。编写function函数，theta_A=pi∕7，theta_B=pi∕7，h=15，R=20，r=10，x0=1，y0=0时，L1=18.8921，L2=19.6445，L3=19.9897，L4=20.6488，L5=19.5517，L6=20.6766。

2.1.2 高度不变，已知杆长求移动的中心点—正解

利用MATLAB中的隐函数符号变量计算，但收敛速度慢，故修改solve的误差限，用2.1.1中的杆长，求得中心坐标，如图5所示。并对比正反解数据，如表1所示。

图5 位置逆解隐函数图Fig.5 Implicit Function Graph of Inverse Position Solution

表1 正解精确度Tab.1 Precision of Positive Solution

数据分析：在表1正反解结果对比中，由于计算数据保留精度的影响，保留4位小数得出的误差仅在0.05%内，说明方法可行，求解结果准确度高。

2.2 旋转坐标变换

上平台在初始状态下与下平台平行，描述在保持上平台初始中心位置不变的情况下，向任意方向倾斜某一角度，此时六根支杆的长度随倾角变化的情况。

画出同一坐标系中的原始坐标和旋转后的坐标，如图6所示。

图6 坐标旋转Fig.6 Coordinate Rotation

绕Z轴旋转：原始坐标为XOY，绕Z轴旋转γ度得到坐标系X'O Y'。Q'为坐标变换Q对应的点，即Q'=R Z,γQ，则

同时，坐标系绕X轴旋转角度α的变换矩阵为：

坐标系绕Y轴旋转角度β的变换矩阵为：

故总坐标系变换矩阵为：

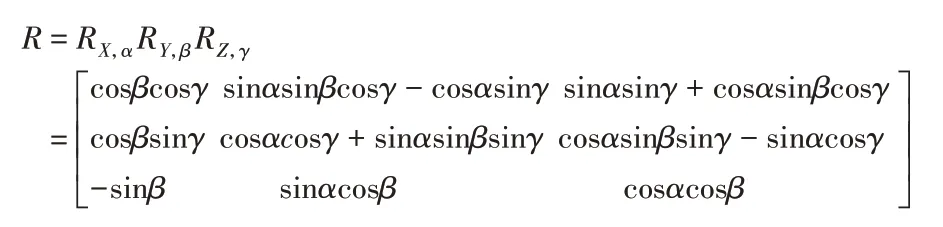
2.3 复合姿态

复合姿态包含坐标轴方向的运动、绕坐标轴旋转的运动及通过某一指定路径实现该姿态。

复合运动变换=旋转矩阵+平移矩阵=R[x0，y0，z0]T+T，式中：T=［XT，Y T，ZT］T，XT，YT，Z T分别是沿X、Y、Z轴移动距离。

3 运动控制与MATLAB∕SimMechanics仿真

SimMechanics拥有一系列的模块库，机械模型和仿真工具。故采用科学计算软件MATLAB中Simulink的SimMechanics对并联机器人进行动态仿真。机器人仿真系统原理图，如图7所示。

3.1 建立机械系统模型

3D模型最终可视化动画化效果图，如图8所示。可以从不同的角度控制鼠标进行查看平台的运动。杆伸缩量结算模块图，如图9所示。编写function函数leg_length.m计算。其中，轨迹规划部分，如图10所示，轨迹规划作为输入，输出为杆伸缩量。用Goto模块（图9）和From模块（图12）代替信号连接线。

图8 MATLAB仿真三维模型可视化Fig.8 Visualization of 3D in MATLAB Simulation

图9 杆伸缩量结算模块Fig.9 Rod Expansion Settlement Module

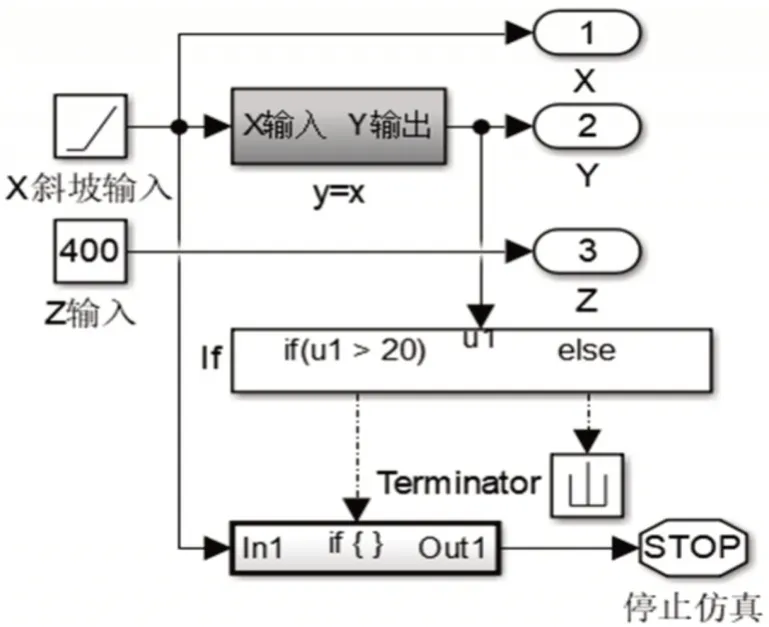
图10 轨迹规划器Fig.10 Trajectory Planner

3.2 执行机构模型

建立平台与支链之间的机械关系，如图11所示。上下平台的参数通过编制m文件设置计算得出，并在CS1至CS6设定参数。运动平台的坐标检测传感器用Body Sensor模块，将其连接到刚体的附加输出端，用以检测运动平台的位置、速度等信息，并且可后接示波器显示出来。Env模块定义环境参数。

图11 执行机构Simulink模块总图Fig.11 General Drawing of Simulink Module of Actuator

以杆4为例，杆件4支链模型，如图12所示。上下杆用Body模块表示为实体，Revolute模块为转动副，约束两个实体间只有转动。Cylindrical模块为柱面副，代表缸（介质为液或电或气）内既可以转动又可以移动。

图12 杆4支链模型连接图Fig.12 Connection Diagram of Rod 4 Branch Chain Model

其中，S输入模块，如图13所示。驱动器Joint Actuator驱动杆运动。

图13 S输入驱动模块图Fig.13 Input Driver Module Diagram

3.3 数据模拟实证

MATLAB仿真获得的Y坐标随时间的变化曲线，如图14所示。轨迹输入为斜坡函数，得到的轨迹与预设轨迹相符，说明仿真结果和解算方法较为理想，轨迹跟踪效果良好，满足预设系统要求。

图14 数据实例模拟Fig.14 Data Instance Simulation

4 结束语

主要对Stewart型六自由度并联运动平台进行了运动学正解研究，首先建立了运动平台空间运动数学模型，提出一种新的正解方法——隐函数图解法，通过MATALB程序求解可快速获得末端执行器的位姿序列。通过数值模拟验证，结果表明，该方法运算效率更高，且误差在0.05%内。之后，建立了MATLAB∕Sim‐Mechanics模型，设计了平台轨迹规划（即轨迹的设定与约束），其内部运动参数均可实现灵活调控，同时又可实现运动姿态可视化，具有Solidworks等软件不可比拟的优越性，经过数值模拟验证，其轨迹与预设轨迹的一致性非常好，与传统方法相比，其对平台的实时控制更加高效准确。该项研究对于并联机器人的正解求解提供了新的思路，有助于这一难点的进一步突破，对Stewart型平台运动分析与控制具有很大的指导意义。