石墨烯热声换能器的有源控制应用
2022-04-27邢倩荷
邢倩荷
(苏州建设交通高等职业技术学校,江苏 苏州 215104)
0 引言
石墨烯热声换能器由铺设在绝缘基底上的石墨烯组成,仅有几十纳米厚,具有透明度高、耐弯曲、无磁等诸多优势[1],可以任意裁剪、悬空或直接铺设在现有的物品上。TIAN 等人制备出纸质基底石墨烯薄膜扬声器,实验研究了石墨烯热声换能器输出声压与输入功率和频率之间的关系[2]。SUK等人通过改变基底表面孔隙度和薄膜弯曲曲率研究了不同基底石墨烯薄膜的发声性能[1]。TIAN 等人成功制备了石墨烯耳机,并利用石墨烯耳机成功实现对狗的训练[3]。相比于传统商用耳机,石墨烯耳机具备频率响应宽和声压波动小的优点[3]。FEI等人成功制备三维石墨烯海绵,实验表明三维石墨烯的发声性能明显优于二维石墨烯[4]。
有源噪声控制一直是噪声控制领域的研究热点。田静以声能量密度为目标函数,探究了单极子次级声源管道的降噪性能[5]。姚加飞、郭静以径向有功声强为控制目标,对单极子声源有源降噪效果的最短距离进行了深入研究[6]。程予露以声功率为目标函数,探究了碳纳米管薄膜声学作动器在噪声控制领域中的应用[7]。
本文基于石墨烯薄膜的声场理论模型,研究以石墨烯热声换能器为基础的有源噪声控制。利用相消干涉原理构建了有源消声模型,以总辐射径向声强为目标函数,通过仿真计算,分析了降噪效果与声源间距、声频率的关系,探究了石墨烯热声换能器在噪声控制领域的可行性。
1 石墨烯热声换能器
将石墨烯薄膜热容量以及基底热损耗纳入影响因素,考虑薄膜瑞利距离R(R=A/λ,A为薄膜面积,λ为声波波长),构建石墨烯热声效应模型,如图1 所示。
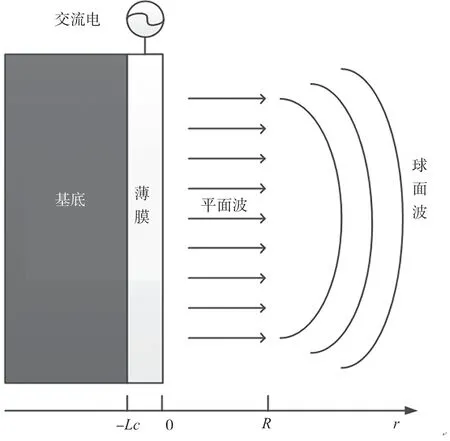
图1 石墨烯热声效应模型
气体为理想气体,不考虑自然对流,得到石墨烯热声换能器的近场声压公式[8]为:

远场声压公式为[8]


2 有源控制模型
在自由空间中有初级声源P和次级声源S,两声源间距为l,如图2 所示。假设这两个声源的声振幅相等,但相位相差180°。M点为空间中任意观察点,声源P和声源S到观察点的距离分别为rp、rs。

图2 石墨烯热声换能器有源控制模型
基于石墨烯热声效应理论模型,根据声波叠加原理,得到耦合声场的总辐射声压为:

若观察点到两声源的距离较远,此时初级声源P和次级声源S所辐射的声波到达观察点时振幅几乎一致,即rp≈rs≈r。但初、次级声源的相位差异不能忽略,即:

当低频段两声源间距l较小时,可认为kl<1,将式(5)代入式(4),可进一步简化为:

初级声源辐射的径向有功声强可表示为:
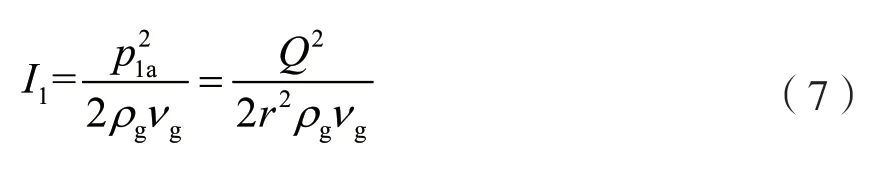
假设M位于次级声源中轴线上,则,那么此时初、次级声源辐射的总声强为:

3 有源控制计算
由式(6)可知,测量距离r和夹角θ都会影响耦合辐射声压,也就意味着在相同测量距离下,方向的改变也会影响测量声压。初次级声源耦合声场的辐射指向性如图3 所示。可以发现,当θ=±90°时,耦合声压为零,此时两声源幅值相等,相位相反;当θ=±180°时,耦合声压最大,此时两声源幅值相等,相位相近。

图3 初次级声源耦合的声场指向性
仿真模拟石墨烯换能器选用2×2 cm2PET 基底。测点设计在初级声源的中轴线上,测距r=40 cm。输入功率设置为10 W,声源间距l=20 cm。计算可得初级声场、耦合声场辐射的声压级,如图4 所示。

图4 声场辐射的声压级
由图4 可知,初级声场的声压级明显高于耦合声场,尤其是在低频段降噪效果显著。当f=200 Hz时,声压级降低了10 dB。但随着频率增加,降噪效果减弱。当f=900 Hz,此时降噪效果为零,这与单极子有源噪声控制理论相吻合[9]。当f>900 Hz,耦合声场的声压级高于初级声场,即石墨烯单极子的有源降噪模型仅适用于低频段。
保持其他条件不变,改变声频率f,频率f与径向声强降噪量ΔI之间的关系如图5 所示。在近间距低频前提下,径向声强降噪量可达到27 dB;但随着频率f的增加,ΔI逐渐减小。当频率达到一定数值后,降噪量几乎为零,这与单极子有源噪声控制理论相吻合[9]。
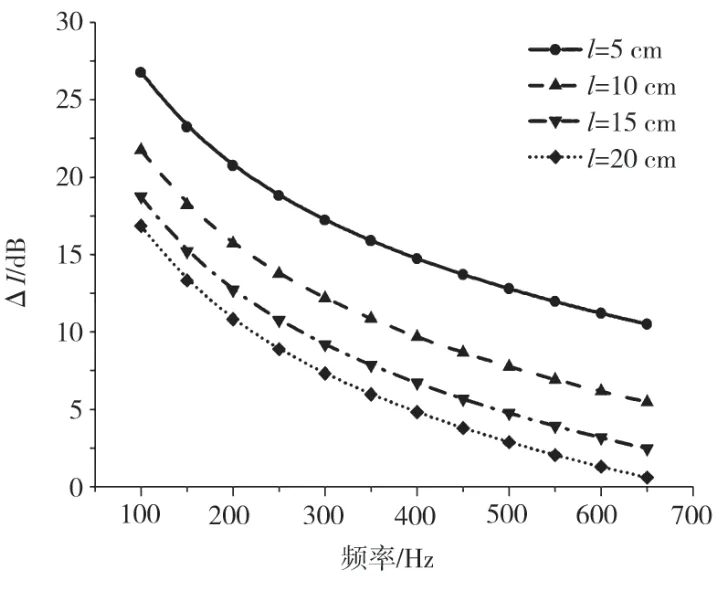
图5 频率与降噪量的关系
随着源间距l 的增加,径向声强降噪量ΔI逐渐减小,有源噪声控制的有效频率范围也就越窄。在相同频率下,l=5 cm 与l=20 cm 的径向声强降噪量ΔI相差10 dB。当声源间距达到一定数值后,降噪量几乎为零。此时应合理布置声源位置,以获取最优降噪效果。
4 结语
本文基于石墨烯薄膜的热声模型,将石墨烯热声换能器视为单极子,应用于有源噪声控制研究领域。利用相消干涉原理构建了有源消声模型,以径向声强为目标函数,分析降噪效果与声源间距、声频率的关系,探究石墨烯热声换能器在噪声控制领域的可行性。主要结论如下。
(1)对于耦合声场,在相同测量距离下,方向的改变也会影响测量声压。当θ=±90°时,耦合声压为零;当θ=±180°,耦合声压最大。
(2)石墨烯单极子的有源降噪模型仅适用于低频段,声压级降低量可达到10 dB;高频段降噪效果下降,甚至会出现耦合声压叠加加强的现象。
(3)径向有功声强降噪量ΔI与声源频率f、声源间距l呈负相关关系。当测量点确定后,声源频率f和间距l可以量化空间中径向有功声强降噪量ΔI。
