基于电流曲线的道岔卡阻识别算法及实现
2022-04-27陈蕊
陈 蕊
(国能包神铁路集团有限责任公司,包头 014000)
道岔卡阻在道岔故障类别中的危险等级是相对较高的,道岔的卡阻意味着道岔无法运动至有效位置,列车倾覆的发生概率将会大幅提高,由于目前大多数岔区未安装检测道岔锁闭是否结束的传感器,因此无法采用传感器检测的方式对道岔卡阻第一时间进行预警。
一个完整的转辙机动作的电流曲线是能够从某些视角反映道岔的移动过程的,由于道岔在各个时刻所承受的摩擦力、钢铁的回弹力是在变化的,因此其所需要的动力也是在不停变化的,这是引起电流曲线变化的主要原因。ZD6 转辙机正常工作下的一个周期完整电流曲线如图1所示。
从图1可以明显看出,在转子转速达到正常运行速度(300 ms 时刻附近)后,整个运动过程的电流维持在1100 mA 左右。当卡阻发生后,离合器内将发生摩擦,由于该摩擦力大于道岔搬动所需要的力,因此电动机需要消耗更多的电能来克服摩擦力,电流曲线将会上移,此时的电流曲线也被称为摩擦电流。在卡阻持续的情况下,该摩擦电流将会持续,直到超时检测发生或人为关断电源。典型的卡阻电流如图2所示。
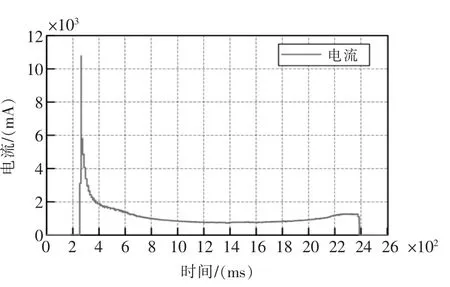
图1 正常的ZD6 转辙机周期动作电流曲线Fig.1 Normal ZD6 switch machine periodic action current curve
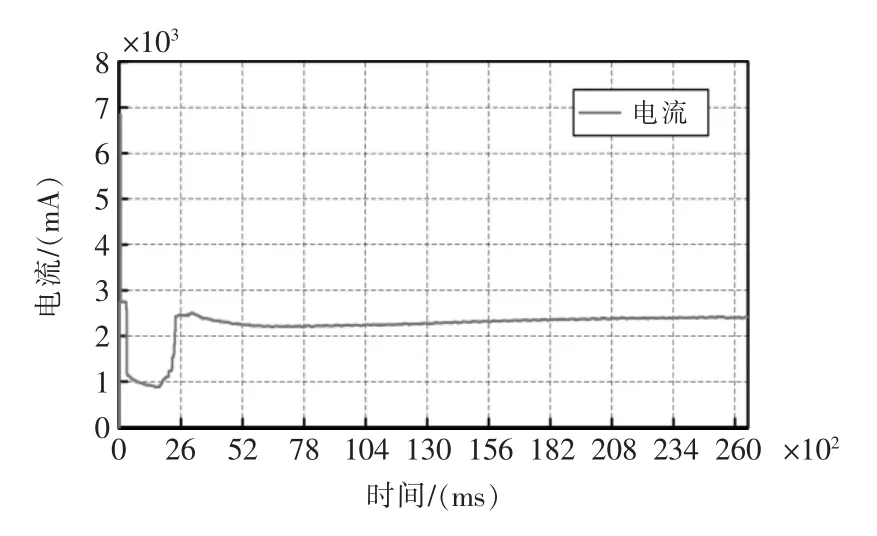
图2 卡阻发生时ZD6 转辙机的电流曲线Fig.2 Current curve of ZD6 switch machine when switch block
图2所示的情形,相对来说是一个较为理想的卡阻电流曲线,实际上由于现场环境复杂,强弱电交叉的场景较为普遍,电流曲线中出现噪点是不可避免的。如果仅采用阈值的方式进行卡阻识别,那么电机启动过程中的尖峰段的部分曲线也是符合条件的,也可能会被误判为卡阻。随着人工智能的发展,出现了大量的基于相似、故障树的识别技术[1-12]。本文通过分析数据特征,采用了一系列成熟的算法对这些特征进行提取,可以在有限的条件下,高质高效地完成电流曲线的特征识别,从而进行进一步的分析和诊断。
1 研究思路
在开始研究之前需要特别指出的是,通过对卡阻曲线和正常曲线对比,卡阻曲线的数据量往往是正常曲线数据量的几倍甚至十几倍,处理的时间也将会大大延长,因此先对数据进行小波分解和重构[13],采用小波降层采样的处理方法既能降低数据量,又能保证曲线形态,从而实现“降维打击”。但并非所有大数据量曲线均是卡阻曲线,因此需要在曲线形态吻合的情况下,才能进行故障定位。
对于常见的电流曲线,将其分为启动阶段、解锁阶段、移动阶段和锁闭阶段。而对于卡阻曲线,由于卡阻的发生与正常曲线之间具有明显的交接线,因此也是可以进行阶段分割。
2 算法设计与实现
本研究以ZD6 的实际电流曲线为例,采用算法设计与实现同步进行的方式对识别方法进行展开说明。
2.1 小波降层采样
小波分析的核心思想为:利用小波尺度函数对原始数据进行阶梯逼近,如式(1)所示,采用多层小波分解算法(如式(2)所示)对逼近数据进行分解,其层分解的逻辑图如图3所示。对数据分层后,以图3所示,从下往上根据所需要的数据量进行截断,最后对函数进行重构。在图3中,越是上层其数据量越大,代表采用的尺度函数的分辨率越高。重构采用的算式如式(3)所示:
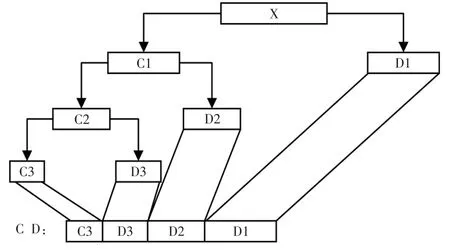
图3 小波多层分解示意图Fig.3 Schematic diagram of wavelet multilayer decomposition
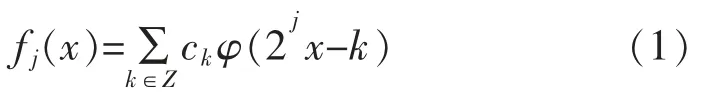
式中:φ 为尺度函数。
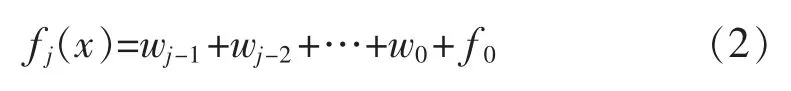
式中:
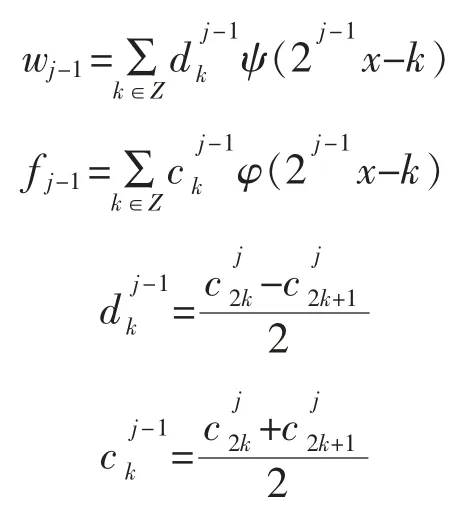
ψ 为小波函数。

式中:

本研究建议采用保留不少于3000 点的最少点数的方式进行小波降层采样,也就是以刚好大于3000 点的层数为截至,得到采样数据。采用本方法对图2数据进行采样,采样后的采样数据如图4所示。其中两侧存在极少点的零值,这是由于降层剔除了高频分量,而该位置的数据为断崖式阶跃变化,因此出现了超高频分量被剔除,导致该位置数据无法中和,各端的零值点数通常是不超过5 个的。在此要说明的是,降维采样数据的点的位置与原位置之间正比于二者数据的个数,因此可得到二者之间的点的对应关系,换算关系如式(4)所示:

图4 卡阻电流曲线的小波降层采样结果Fig.4 Wavelet laydown sampling results of the switch block current curve

式中:xold为原始位置点;xnew为降层采样后位置点;Nold为原始数据点总数;Nnew为降层采样后数据点总数。
2.2 降噪处理
由于采样点具有纹波的抖动特点,所以需要把这些抖动幅度进行降低。同时在多个位置电流曲线具有“阶跃”式变化,因此无法采用低通滤波方式进行滤波(阶跃信号含有所有频率分量,低通滤波依然产生伴生波形),为此本研究采用求累积求和量的方法对电流曲线进行处理,算式如式(5)所示:

2.3 高通滤波
可以看出,累积曲线发生转折的位置即为电流曲线发生大跳跃的位置,如果对数据进行去趋势处理后(去除直流量),则曲线发生转折的位置将会被放大。这里采用了Butterworth 高通滤波,其频幅相应曲线如图5所示,进行累积曲线与高通滤波后曲线如图6所示。

图5 Butterworth 滤波器频幅响应Fig.5 Frequency response of Butterworth filter
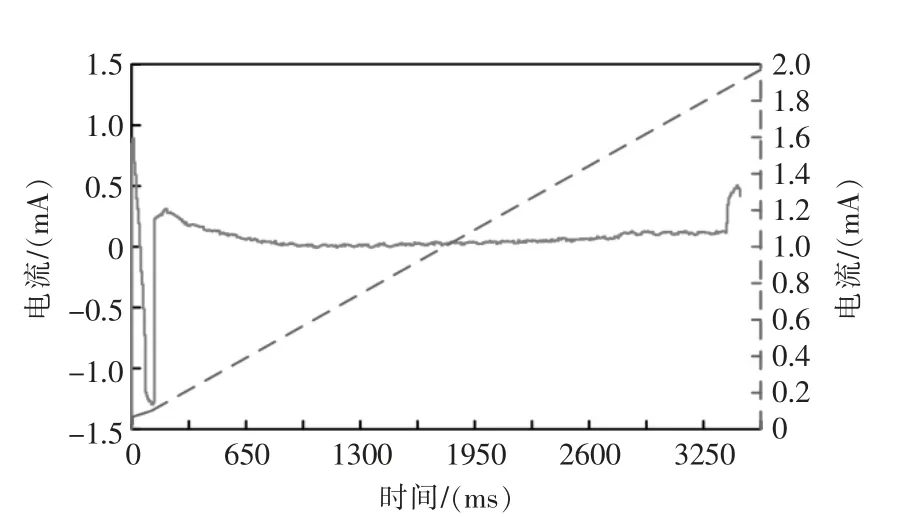
图6 滤除直流量的累积曲线Fig.6 Cumulative curve for filtering out direct flow
2.4 区域粗分割
高通滤波后的曲线的峰值(波峰或波谷)对应着累积曲线的拐点位置,这些拐点位置也对应着电流曲线的阶跃位置。可以看到由于滤波的缘故,在幅度较大的尖峰附近存在伴生的小波尖峰,在数据结尾处存在一个尖峰。
本研究采用五点极值法求取峰值位置,方法如下:
某点Pi,其值大于0,且其值与左侧2 个点呈递增趋势,与右侧2 个点成递减趋势,且连续5 个值不能全部相等,则称为正向极值,条件表达式为
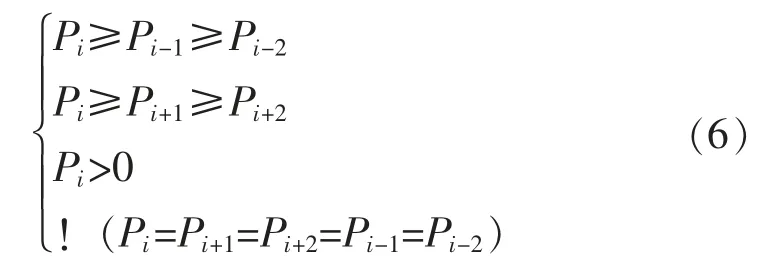
某点Pi,其值小于0,且其值与左侧2 个点呈递减趋势,与右侧2 个点成递增趋势,则称为负向极值,条件表达式为
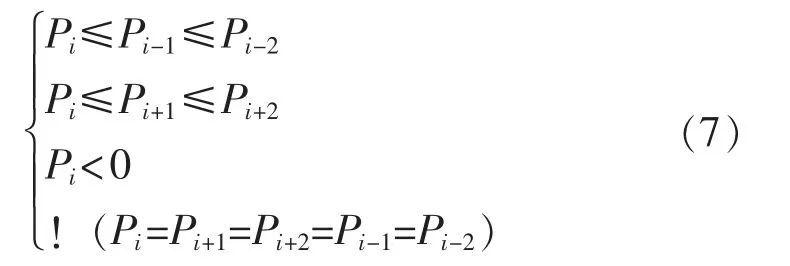
从图6中可见,对于为了降低中间段的纹波对驼峰提取的影响,采用KS 密度函数法对其进行分类,如图7所示。去除靠近x 轴范围内的数据,降低纹波对其驼峰求取的影响。去除0 位置的纹波的数据后,新的滤除直流量的数据如图8所示。
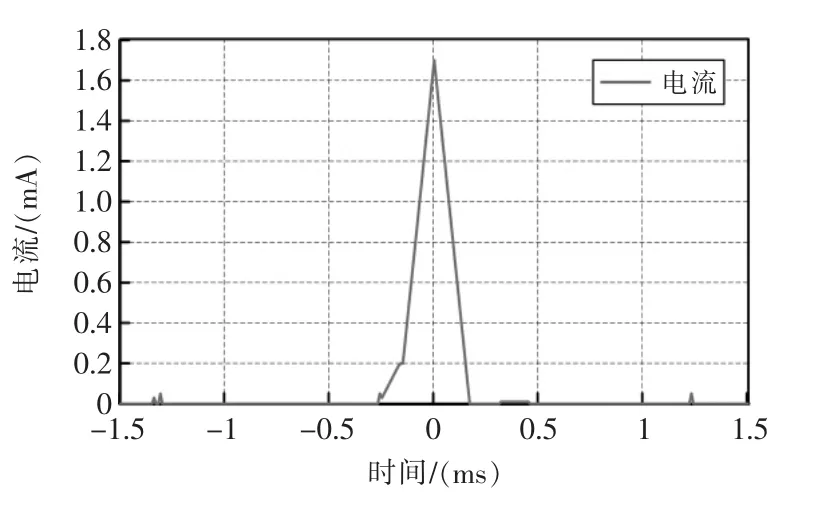
图7 KS 密度函数计算结果Fig.7 KS density function calculation results
求取图8中的峰值后,以各峰值作为界限,即实现了将电流曲线以跳跃点较大的位置分段的方法。加入分段结果后的电流曲线如图9所示。
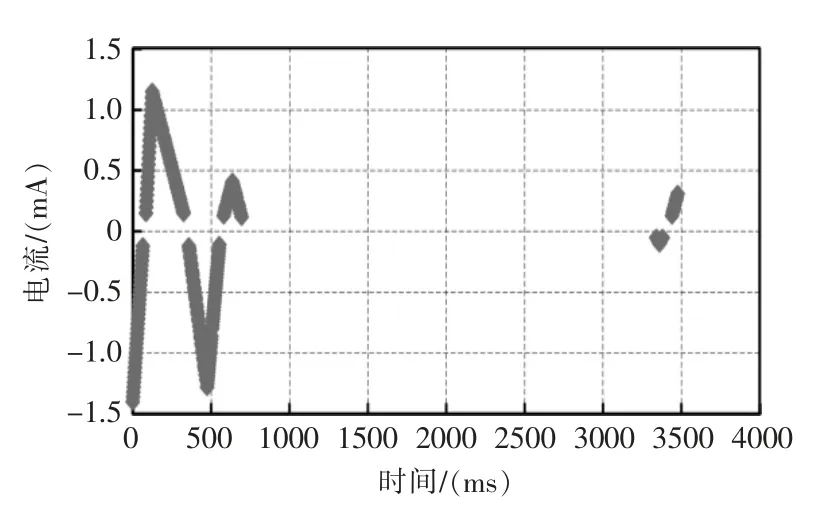
图8 去除纹波后的驼峰图Fig.8 Hump diagram after ripple removal
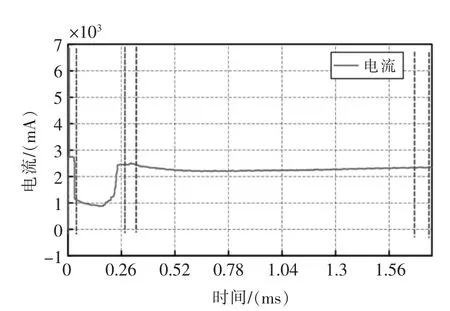
图9 加入分割线后的原始电流曲线Fig.9 Original current curve after adding the dividing line
在图9中可以看到,在第一区段内,右侧的数据是存在强烈波动的,但是其始终围绕着本区段内的“主值”,实际上仔细观察图6中的高通曲线,对应剧烈波动位置的尖峰是确实存在的,只是其尖峰被更明显的尖峰“掩盖”了。这种情况在下面步骤中是有处理的。
2.5 卡阻区段细分
为了消除初级分段造成的范围不准确,需要对初分后的区段进行二次细分。
对大量的摩擦电流分析后,得出常规情况下摩擦电流的曲线具有的4 个规律:
(1)连续的;
(2)持续范围较长的;
(3)纹波小;
(4)水平趋势稳定。
利用第(3)和第(4)条规律,本文再次采用KS密度函数对初级分割的范围内符合的电流值进行分类,以初级分段求得的第一区间的数据为例如图10所示,做KS 密度函数分布如图11所示。

图10 初分第一区间原始数据放大图Fig.10 Enlarged view of original data in the first interval of initial division
从图11可以看出,数据段形成了3 组围绕其某主值分布的集合,也就是整段的数据被分为了3 个范围。求得其中所有的尖峰,则可以得到每个分类区间的“主值”,找到该尖峰与其它峰之间的分界,即每个尖峰的两侧的“山谷(山坳)”位置,为了防止范围过宽而导致无效数据可能被误包含,因此建议从峰值对应x 轴位置向左右两侧最多延伸不大于±150 mA 的范围,这样就得到了每个尖峰及其能控制的范围,即得到了整个区段内数据被分类后能覆盖的多个(也可能是一个)数据范围。
图11 第一区间内的KS 密度函数分布图Fig.11 KS density function distribution in the first interval
将求得的分类范围与摩擦电流范围进行对比,将二者之间存在包含、交叉关系的分类范围作为重点研究对象,因为发生摩擦电流的区段内的数据一定位于这些分类范围内。
经过筛选后,通常只会有一个分类区间是符合上述条件的。为了防止发生误判,如果发生多个区间符合条件的情况,则加入阈值判断,即交叉范围的比例低于某一阈值的情况则认为该区间内并未发生摩擦电流。
获得有效范围后,剔除不在该范围内的数据,剩余数据如图12所示。其中“■”状数据为筛选后的数据,线型为原始电流数据。

图12 KS 密度函数筛选前后的电流曲线Fig.12 Current curve of KS density function before and after screening
从图12可以看到,虽然某些部分数据是属于摩擦电流的范围,但其并不是由摩擦导致的电流数据,因此不能构成有效卡阻区间。由于摩擦电流是稳定的,其总趋势应呈现出水平直线的形态,所以建议先采用线性回归法对值的变化趋势做出判断,如果拟合结果的斜率是相对较大的,那么就证明本段数据并不平稳,仅是一个穿过有效范围内的曲(直)线,违背了第(4)条规律:“水平趋势稳定”,其本质是一个过路者。本文根据大量的算例,认为斜率大于0.1 的情况,即便其平均值在有效范围内,也不属于摩擦电流范围。
由于摩擦电流是连续的,因此很容易通过判断图12中“■”点的序号是否连续,对其进行分组。本文认为某一分组中点数少于3 点,则该组是噪点。
对分组内的数据做线性拟合,拟合结果与原始数据对比如图13所示。

图13 拟合线和原始数据的比较Fig.13 Comparison of fitting line and original data
常用的线性回归通常采用最小二乘法计算,以方差作为最终目标,找到能够使得方差最小、最稳定的一元一次多项式,本研究也采用了该方法[14]。
2.6 摩擦电流发生的判别
出现摩擦电流并不就代表一定发生了卡阻,卡阻发生在出现持续一段时间的摩擦电流后。实际在正常的情况下,在锁闭阶段也可能由于密贴调整的不完美发生一小段的摩擦电流,这种情况可以认为是正常现象。因此对于摩擦电流发生的时长要进行确认,本研究针对ZD6 常用的场景,认为如果摩擦电流持续在2000 ms 以上即可认为发生了卡阻。
本研究的全局流程如图14所示。

图14 全局流程Fig.14 Global flow chart
对图1原始数据的卡阻段的识别结果如图15所示,图中的粗线就是识别结果。对图1原始数据最终的分析结果如表1所示。
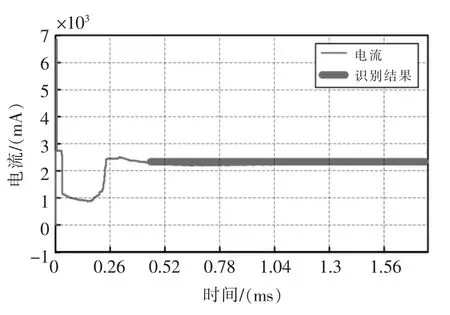
图15 卡阻的识别结果Fig.15 Identification results of switch block
由表1可见,在分区段时,由于高通滤波的扰动,曲线后半段被分割成了多端,可以看到这些段之间的起终点是相互衔接的,因此对图14的处理流程做以下修正:

表1 识别卡阻区段信息Tab.1 Identify the jammed segment information
(1)在判断是否该连续数据为卡阻时,不再判断“连续数据的长度>阈值”;
(2)对不考虑条件(1)的所有卡阻进行首尾衔接识别,如果首尾是衔接的,则拼成一个新的连续数据;
(3)对步骤(2)中形成的新数据判断“连续数据的长度>阈值”,最后得到卡阻的识别结果。
新的处理流程如图16所示,最终识别结果如表2所示。

表2 修正后识别卡阻区段信息Tab.2 Identify the jammed segment information of after correction

图16 修正后的流程Fig.16 Revised flow chart
可以看到组合后,只存在一个卡阻区段,该段总点数为22802 点,采样速率为800 Hz,时长为28.5 s,可根据阈值判断是否为卡阻,本研究推荐2 s以上的摩擦电流为卡阻导致,因此认为图1中数据发生了28.5 s 的卡阻。
3 实验验证
在包神铁路万水泉南站,对16/18# 道岔进行卡阻模拟实验,得到故障电流曲线如图17所示,经算法分析判断,诊断出道岔发生卡阻。
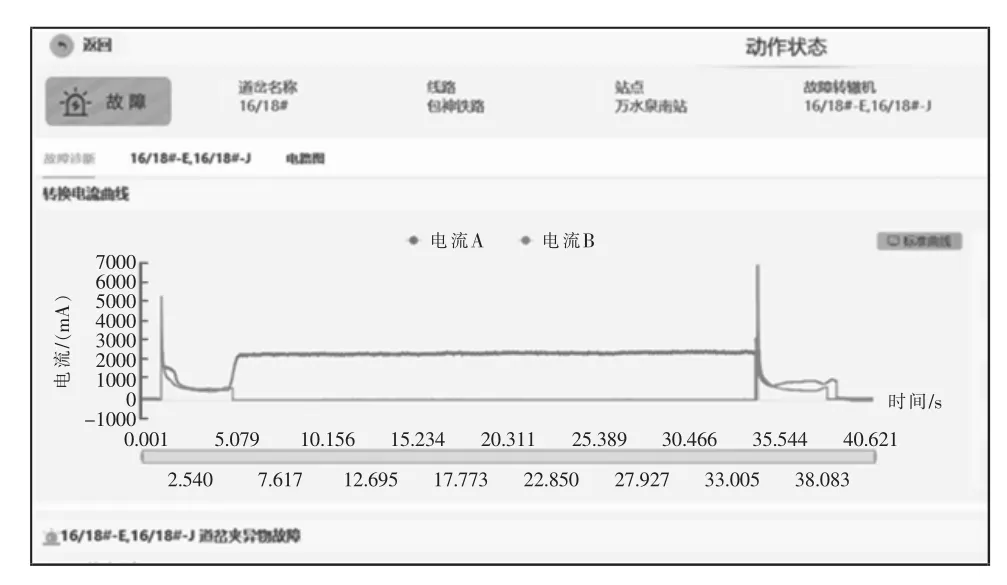
图17 道岔夹异物故障实验电流图Fig.17 Current diagram of turnout clip foreign body fault experiment
4 结语
本研究从实际出发,首先对道岔卡阻将会产生大数据量的情况,给出了小波降层采样的处理方法。通过两次使用KS 密度函数,对电流数据累积量的数据高通滤波后查找峰值、区段内数据值分组进行处理,有效地降低了由于数据波动及区段分割位置的数据阶跃特征带来的影响。
最后采用线性拟合方式,对“过路”摩擦电流进行了剔除,大大地提高了识别的准确率。同时本文提出的摩擦电流的4 个规律,对道岔卡阻的识别起到了决定性的指导作用。
