液体薄层中环链状空化泡云结构稳定性分析*
2022-04-27李凡张先梅田华胡静陈时王成会郭建中莫润阳
李凡 张先梅 田华 胡静 陈时 王成会 郭建中 莫润阳
(陕西师范大学,陕西省超声学重点实验室,西安 710062)
为分析超声空化的薄层液体中稳定的环状气泡链结构,本文考虑气泡间次级声辐射影响,得到了表征气泡间相互作用的气泡基本动力学方程以及次Bjerknes 力的表达式,数值分析了气泡平衡半径、声波频率和声压对纯液体区可能出现的单气泡所受的次Bjerknes 力,发现环形泡链能够吸引液体区内的新生的半径小于2 µm 的气泡,这可能是一定条件下环形气泡链能够稳定存在的原因.随着驱动声波压力增加,气泡数密度增加,气泡间的耦合作用增强,液体区内的环形泡链结构可能被液体区内出现的大气泡或者气泡团破坏,进而导致环形结构演变成柱状、雾状乃至整个液体区均充满空化泡的情况发生.通过高速摄影机观察了强声场作用下换能器辐射面外侧液体薄层内空化初生至形成空化云团簇的整个过程,在空化云团簇中发现了局部同步崩溃并形成类纯液体薄层的现象,该液体薄层边界随时间振荡持续约4 个声周期后被空化云团簇吞没,局部类纯液体区出现的位置具有随机性.实验观察结果和理论预测具有很好的一致性.
1 引言
液体中的微小气泡核在声波的作用下会表现出生长、振荡和内爆等一系列的动力学过程.气泡的瞬间塌缩使其内部出现高温高压[1],在其周围产生微射流与冲击波,这些效应可应用于化工[2]、医学[3]等领域.合理利用空化效应须先了解气泡在声场作用下的振动情况,从Rayleigh 开始,多位学者对单气泡的振动进行了研究[4].实际能利用的超声空化泡通常以分布不均匀的泡群形式存在[5],如链状结构[6].An[7]利用微分关系,导出了一维气泡链与球状气泡群中气泡的动力学方程,并且通过计算势能与等效弹性系数对一维气泡链的稳定性进行了分析[8];大功率工作状态下换能器辐射面附近可形成锥状泡群,且在辐射面表面处存在一柱状气泡云分布区,基于气泡的耦合振动特征可得到柱状薄层泡群的气泡动力学方程[9],分析气泡的声响应;从KZK 方程出发可得到换能器附近的声场分布[10],并基于声场分布和次级Bjerknes 力[11]解释锥状气泡群的现象.
柱状与锥状气泡群均为三维稳定结构,细节变化难以观察,不利于分析.而换能器与固体壁之间液体薄层中的准二维空化结构容易清晰观察到[12],有利于从宏观角度更好地认识空化现象.薄层结构可以增强空化效应[13],利用此效应可增强纺织品的清洗效果[14].气泡在薄层中崩溃会对材料边界产生冲击,因效果类似于喷丸[15],所以称其为空化喷丸,可用来提高材料表面的疲劳强度,相较于传统喷丸工艺还具有众多优点[16].Gao 等[17]研究了换能器振幅对材料表面参数的影响,发现超声空化喷丸可以显著提高工件表面硬度,而表面粗糙度增加不明显.空化效应与气泡的振动状态密切相关,因此对薄层中气泡群的动力学与稳定结构进行研究具有重要意义.Wu 等[12]利用高速摄影机观察了不同厚度的薄层气泡群的稳定结构,发现点状、圆盘状、杆状等不同形貌的泡群结构且具有宏观稳定性.Bai 等[18]对圆盘状结构进行了解释,他们认为主Bjerknes 力推动气泡向气泡云移动;次Bjerknes力为吸引力,且其合力的效应类似于表面张力,所以气泡云边界保持圆形.
气泡云结构受到彼此间耦合振动的影响,形成的次Bjerknes 力具有调控作用.为从理论角度解释Wu 等[12]的实验现象,本文构建描述环链状气泡群稳定结构的理论模型,从基本动力学方程出发分析空化场中气泡所受的次Bjerknes 力,探索空化场中声场条件变化引起泡群结构稳定或者演变的本质.同时,利用高速摄影机观察了薄层液体中强声场作用下的空化泡分布行为,以印证本文的理论分析.
2 理 论
液体中的气泡振动将会在介质中形成次级声辐射,其辐射压强可表示为[19]

式中ρ为介质的密度,dij为气泡i与气泡j之间的距离,Ri为气泡i的半径,上标点表示对时间微分.液体空化场中由于声场分布的影响可形成稳定的空化泡群结构,如薄层液体在一定的压力作用下可形成类圆环型气泡云[12],如图1 所示,圆环内为纯液体区域,环上气泡数密度较外侧带状气泡云区大,因此,为简化描述,将薄层液体空化云区表示成3 个区域,即数密度较大的环形气泡链为Ⅰ区,环形气泡链外侧的气泡云为Ⅱ区,纯液体区域为Ⅲ区近似为圆盘状.为分析形成图1 所示气泡云分布的机理,假定在纯液体区域存在1 个单气泡,分析单气泡与类圆环型气泡团内气泡间的相互作用,探索单气泡被圆盘状液体外侧区域气泡吸引并形成稳定结构的参数条件.
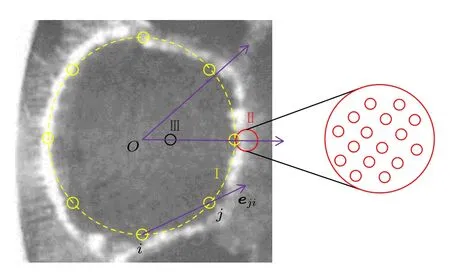
图1 薄层气泡群分区Fig.1.Regional division of thin-layer bubble groups.
气泡的次级声辐射会作用于介质中的其他气泡,形成彼此间的耦合振动,动力学行为可用修正的Keller-Miksis 方程[20]来描述,即

式中c为介质中的声速,Piint/ρ为耦合作用项.气泡壁外侧液体压力可表示为
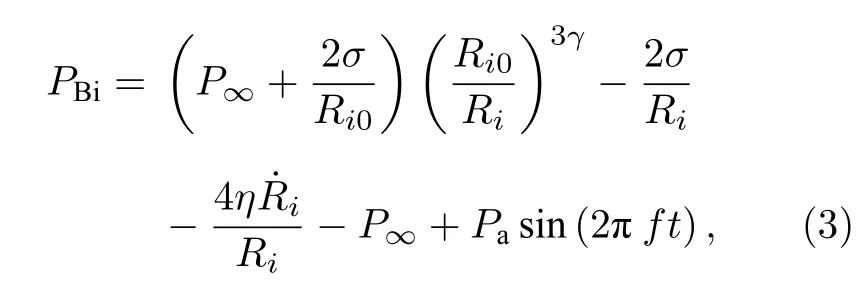
其中P∞为环境压力,γ为气体绝热指数,σ和η分别为液体表面张力系数和黏滞系数,Pa和f分别为驱动声波压力幅值和频率,i=1,2,3 分别代表区域Ⅰ,Ⅱ,Ⅲ内的气泡.
由于声屏障的影响,在气泡云团中,气泡仅与其周围有限范围内的气泡发生相互作用,因此在分析Ⅱ区气泡的振动时,假定作用半径为δr,并假定气泡云轴对称分布,则对Ⅰ区和Ⅱ区振动气泡而言,其动力学方程中耦合项
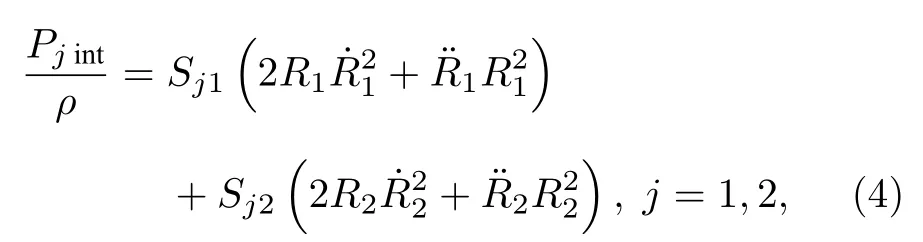
式中Sji(i=1,2) 为气泡i对气泡j的耦合作用因子[21],可分别表示为[22]
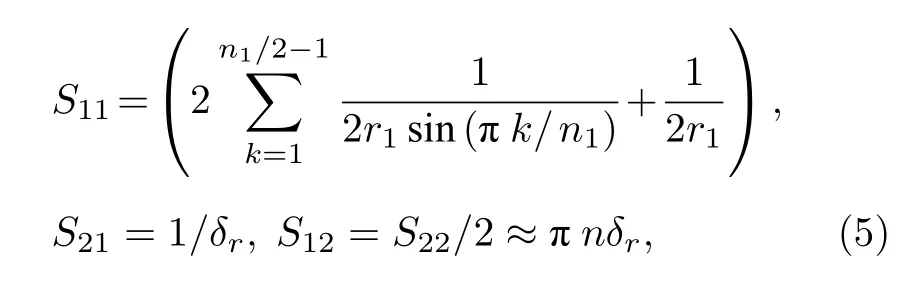
其中n1为内侧气泡链上的气泡个数,r1为气泡链的半径,n为Ⅱ区气泡数面密度.
对纯液体区域内的单气泡而言,仅考虑环形气泡链上的气泡对其的次级声辐射影响,则
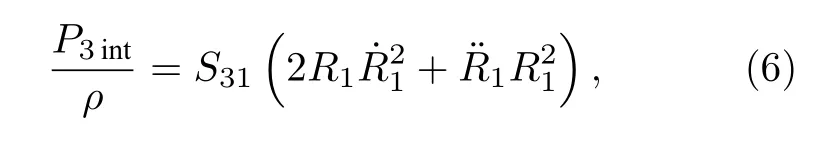
式中耦合系数S31可近似表示为
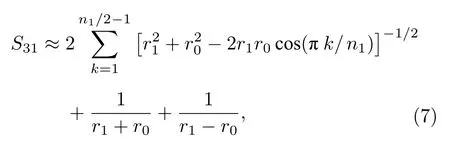
其中r0为Ⅲ区内气泡到其中心距离.
为简化分析,假设气泡云区内所有气泡具有相同的平衡半径,则有
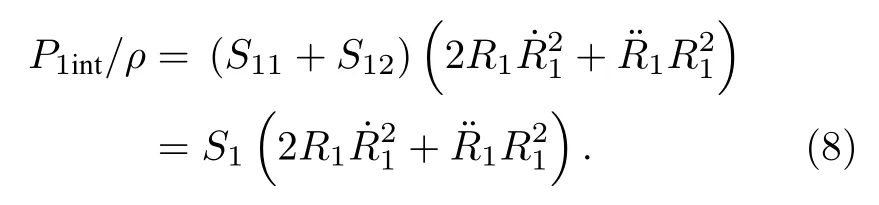
本文的理论分析将分为两步,一是分析纯液体区域内出现的单气泡被环状气泡云区气泡吸引后溢出液体区;二是分析环形气泡链稳定结构形成的原因,此时,不考虑纯液体区域可能出现的气泡的影响.由于气泡云生成于与换能器辐射面平行的薄层液体中,可近似认为气泡云区域内声压分布均匀,因此,气泡云结构的调控主要受气泡次级声辐射引起的次Bjerknes 力的影响,其表达式为
其中Vi(j)为图1 中三个区域内气泡的体积,er为两气泡中心连线方向的单位向量,气泡i对气泡j的作用力正方向如图1 中箭头所示.〈〉 表示时间平均.
3 气泡链形成的机制分析
基于动力学方程(2)可分析气泡的声响应,数值分析所用参数设定为ρ=998 kg/m3,c=1500 m/s,σ=0.0725 N/m,η=0.001 kg/(m·s),P∞=101 kPa,γ=1.4.
基于气泡云分布的对称性假设知,纯液体区出现的单气泡受到环状泡群对它的次Bjerknes 力将沿着以液体区域中心位置为极坐标原点的径向.气泡的耦合系数与气泡的分布有关,根据参考文献[12]实验观察到的气泡数密度分布情况,结合(5)式与(7)式,可取S1=8.5×104m–1,S31=4×104m–1.
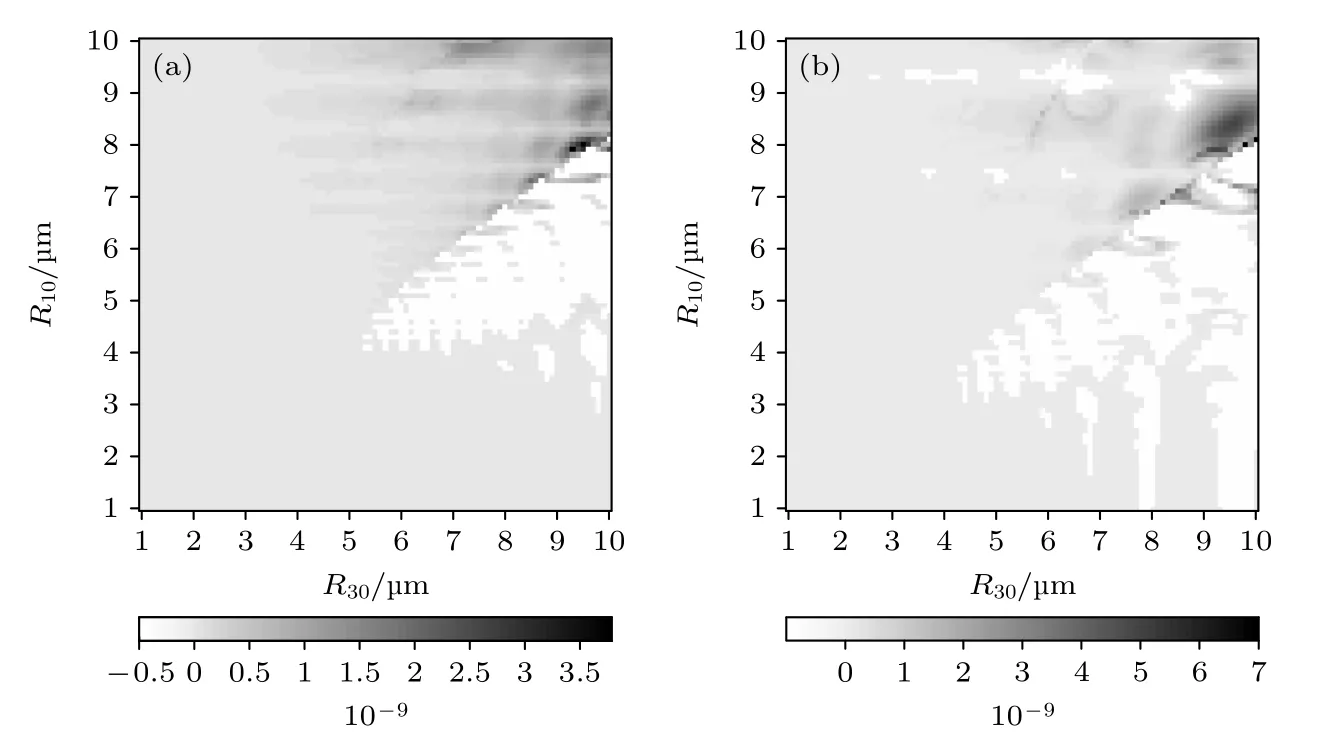
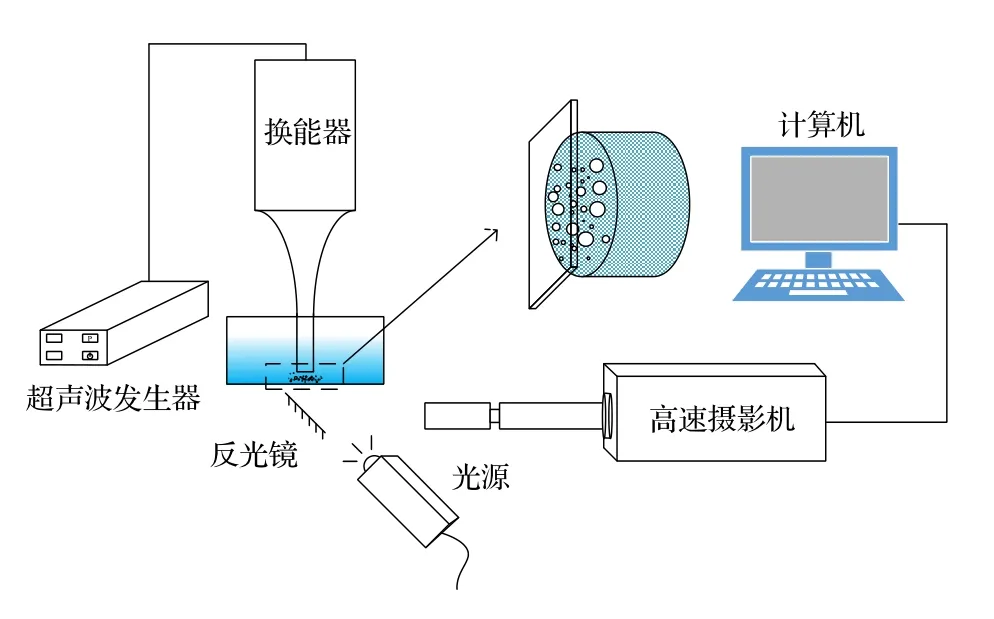
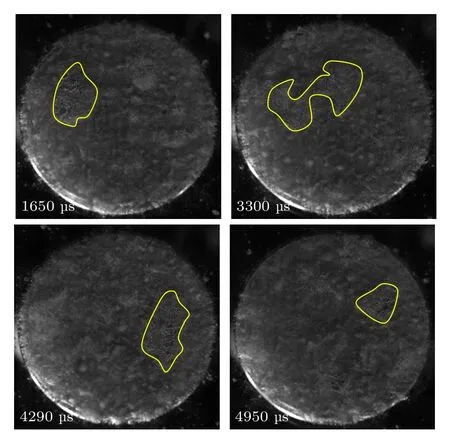
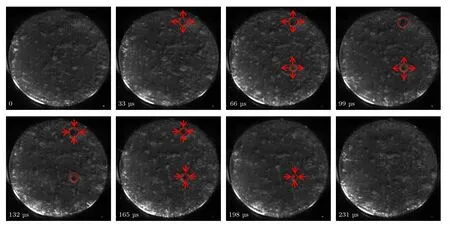
当驱动声波频率为20 kHz 时,液体区内的单气泡所受的次Bjerknes 力随气泡半径变化如图2所示,灰度图中白色区域表示FBr <0,黑色区域表示FBr >0 .从图2(a)可以看出,当驱动声波压力为100 kPa 时,尽管空化泡的非线性振动较弱,但液体中可能出现的单气泡主要表现为被环形泡链上的气泡吸引,仅有在大约 6µm 图2 声波频率 f=20 kHz,液体区域内单气泡所受的次Bjerknes 力随气泡半径的变化 (a) Pa=100 kPa;(b) Pa=120 kPa;(c) Pa=140 kPaFig.2.Secondary Bjerknes force of a single bubble in the liquid area varies with the bubble radius,f=20 kHz :(a) Pa=100 kPa;(b) Pa=120 kPa;(c) Pa=140 kPa. 随着驱动声波压力的增加,液体薄层内的主声场逐渐增大,空化泡生长速度加快,气泡振动增强,气泡间的相互作用也将变得更加剧烈.因此,在极短时间内,纯液体区域内可能会激发出大气泡,进而出现气泡链上的气泡被纯液体区域内的大气泡吸引,导致气泡链上的气泡溢出的现象发生.实际上,液体中的气泡可能与周围气泡聚合成更大的气泡,或大气泡碎裂成许多小气泡.若在较小的区域同时出现一定数量的小气泡,在未被吸引至气泡链处时,可能聚合成大气泡;这时如果气泡链气泡与大气泡半径组合处于主排斥区,可能会在液体区出现由这些大气泡组成的气泡团.文献[13,24]在实验中也可观察到此现象,但大气泡团也会碎裂为小气泡,再次被吸引出液体区. 随着驱动声波频率的增加,气泡之间的相互作用变得更加复杂.对比驱动声波频率分别为20 kHz(图2(a)),40 kHz (图3(a))和80 kHz (图3(b))可以看出,灰度图中白色区域逐渐由单一区域演变成散发的片状区域,且主排斥区对应的纯液体区域单气泡的最小半径有左移的趋势.灰度图随频率演变趋势表明,随着驱动声波频率的增加,稳定的片状纯液体区域的形成相对难[24],也更容易受到气泡聚并或分裂的影响,从而促进环状泡群分布结构向棒状或雾状结构的演化. 图3 驱动声压 Pa=100 kPa,驱动声波频率对单气泡所受的次Bjerknes 力的影响 (a) f=40 kHz ;(b)f=80 kHzFig.3.Driving amplitude Pa=100 kPa, influence of driving acoustic frequency on the secondary Bjerknes force applied to a single bubble:(a) f=40 kHz ;(b) f=80 kHz . 事实上,气泡链的稳定半径受多种因素影响,主要取决于液体性质、驱动声波声场参数以及薄层厚度等.空化场中空化泡的数量与驱动声波压力呈正相关关系[25].为探讨空化泡数密度对液体薄层内空化云分布的影响,取气泡数面密度[12]分别为5×105,1×106和 5×106m–2.分别对气泡分布区内初始半径为R10=R20=3µm 和R10=5µm,R20=3µm 的气泡组合形成的气泡云对应的环状链半径随声压变化趋势进行数值分析,结果表明:气泡数密度越大,环状气泡链半径越小,以至最终可能消失,如图4(a)和图4(b)所示.当气泡链和链外侧气泡半径存在差异时,气泡链半径对声场的响应也会发生变化,如果气泡链外聚集较大半径的空化泡,则在惯性空化阈值(约1.2 atm,1 atm=1.0×105Pa)附近气泡链半径变得极不稳定(图4(c)),气泡链可能无法形成.基于此,我们预测,在观察到稳定的环状泡链空化云结构时,气泡分布区内的气泡半径的可能情况为泡链上半径与泡链外侧半径相同或气泡链上气泡半径大于外侧云区内的泡半径.本文模型关于气泡数密度的增加破坏环链状气泡云结构的预测与实验观测结果一致[24]. 图4 不同气泡半径时,气泡数密度对气泡链半径随声压演变规律的影响,声波频率 f=20kHz (a) R10=R20=3µm,(b) R10=5µm,R20=3µm,(c) R10=3µm,R20=5µmFig.4.Effect of bubble number density on the evolution of bubble chain radius with acoustic pressure for different bubble radius,f=20 kHz:(a) R10=R20=3µm,(b) R10=5µm,R20=3µm,(c) R10=3µm,R20=5µm . 为观察薄液层内的空化结构及其演变,构建了如图5 所示的实验装置,装置主要由超声波发生器与换能器、光源、水槽、反光镜、高速摄像机等组成.液体薄层厚度约为1 mm.利用超声波发生器与换能器(宁波清大超声科技有限公司)产生超声波,辐射面直径20 mm,振动频率20 kHz,最大输入功率3000 W,由高速摄像机(FASTCAM NOVA S16type 200KS-M-64GB,Photron Ltd.,Japan)以30000 帧/s 的帧率,1024×512 的分辨率记录空化结构. 图5 实验装置示意图Fig.5.Schematic diagram of experimental setup. 打开换能器系统工作开关,高速摄像机同时开始记录换能器辐射面外薄层液体区域内的气泡生长情况.从高速摄影机传来的实时图像中可以观察到,由于换能器辐射面振动的影响,表面上粘附的气泡在声波的激励下振动,随即在其周围形成局部的空化泡团聚集;随着超声波发生器瞬时功率从0 逐渐增大,视场中的气泡逐渐增多;经过短暂的时间后,超声波发生器功率稳定在600 W 左右,此时,观察到液体薄层几乎被气泡充满.薄层内气泡云随着声波驱动周期性振荡,局部厚度随着气泡崩溃的不均匀分布而发生变化,因此,在气泡云演变的时序图中观察到气泡局部稀薄的现象,如图6 中亮色曲线所围区域所示.稀薄区出现的位置随机且形状并不固定,其演变行为受到主声场以及气泡间次级声辐射相关的Bjerknes 力的调控影响,导致局部气泡云剧烈崩溃的现象发生.因此,即使在小区域薄层空化云的演变也是非常复杂的,主要表现为气泡云内空化泡并不同时崩溃,每个气泡振动行为与其局部声场环境密切相关.在强声场作用下的液体薄层内也观察到了直径约为1 mm 的盘状气泡分布极为稀薄的液体区,液体区边界对应于环形泡链,其随时间振荡持续约4 个声周期后消失,如图7 中红色虚线围成的圆形边界所示,箭头表示边界移动方向.与低声压情况[24]比较可以发现,本文观察到的高声压、高气泡数密度情况下的环状链半径较小,这与图4 预测的理论结果一致. 图6 薄层液体中的空化结构Fig.6.Cavitation structure in a thin layer of liquid. 图7 薄层液体中的空化结构随时间的变化Fig.7.Variation of cavitation structure in thin layer liquid with time. 环形泡链的消失可能与液体区内出现的大气泡或气泡团有关.在观察气泡云演变的过程中发现了图8 所示的局部弧状泡链围成的纯液体区,以及薄层液体区外气泡团被吸引向气泡云分布区移动的现象.随着气泡团进入该纯液体区并接近弧状泡链,彼此间的相互作用增强,泡链上的气泡被气泡团吸引并溢出泡链,最终气泡团与泡链融合,泡链结构受到破坏,纯液体区域减小以至消失.空化场中气泡的振动行为是超声波众多应用的理论基础,本文实验观察到的现象表明,在一定的外场作用下气泡间的相互作用机制可基于次Bjerknes 力分析,尽管它不是唯一的影响参量,但在空化云分布的局部结构调控中有非常重要的作用. 图8 气泡云吸引周围气泡团Fig.8.Bubble cloud attracting the surrounding bubble cluster. 本文构建了分析超声空化场中环状泡链结构稳定性分析的理论模型,从次Bjerknes 力出发讨论薄层液体区空化场中出现纯液体区域的原因.基于本文理论分析知,环状泡链能够吸引纯液体区内新生气泡核,进而限制了纯液体区内气泡生长为大气泡并稳定存在的条件,然而,局部可能出现的大气泡或泡团也可能破坏气泡链的稳定结构,导致环形气泡链消失并演变成柱状或雾状结构.驱动压力的增加可引起液体薄层内空化泡数密度增加,最终破坏气泡云分布的局部微结构甚至空化泡充满整个薄层液体区.尽管如此,由于声场中气泡间相互作用的影响,次Bjerknes 力的调控作用导致在高密度的薄层液体气泡云中出现局部的类纯液体区,该区域内气泡数密度较低,我们认为是局部气泡同步崩溃的结果.本文的理论分析有助于更好地解释超声喷丸等应用中出现的声空化行为.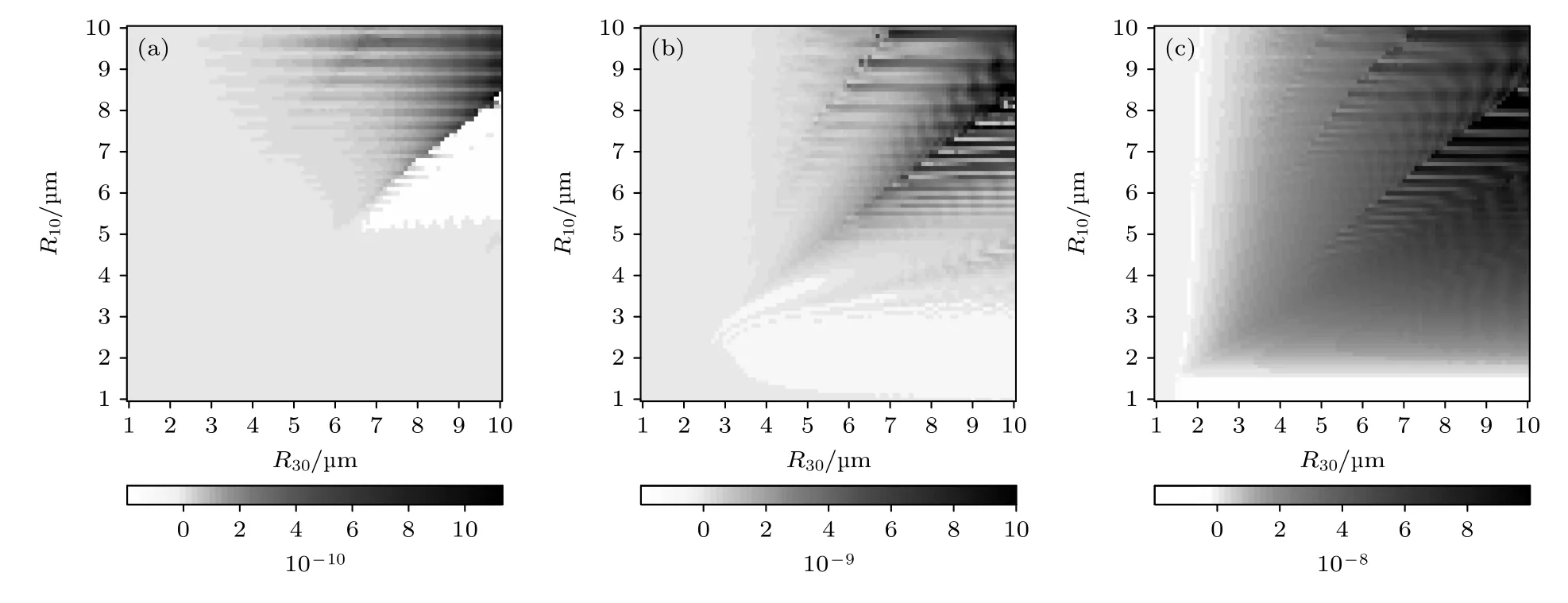

4 强声场中薄层液体内气泡云的实验观察

5 结论
