六自由度运动平台运动学建模与仿真分析
2022-04-27刘喜藏马铭泽
刘喜藏, 马铭泽, 林 皓
(航空工业第一飞机设计研究院,陕西 西安 710089)
飞行模拟器作为重要的地面仿真设备,是典型的人在回路实时仿真系统。六自由度运动平台作为飞行模拟器的重要组成部分,其根据飞机的飞行状态进行实时解算并控制平台进行俯仰、滚转、偏航、升降、纵向和侧向平移运动,从而为飞行员提供瞬态过载感受[1]。六自由运动平台的结构形式多种多样,其中并联结构形式因其具有精度高、刚度大、运动速度快等特点而被广泛应用。并联结构六自由度运动平台的控制目标与作动系统之间是较为复杂的非线性关系,建立运动平台的运动学关系是进行系统结构设计、运动误差分析和实现系统精确、快速控制的重要前提条件。
针对并联结构形式的运动学研究具有逆解容易、正解难的特点,目前已有大量学者开展了相关研究,综合近年研究成果,可划分以下3类:数值法、解析法和基于高级算法的求解法[2]。其中,最典型的数值法便是牛顿迭代法,其求解原理简单易懂,只要迭代次数足够,就能求得满足精度要求的方程解,但迭代初值的选择会影响该方法的迭代速度和寻优结果。陈晓江[3]通过将运动学正解方程表示为9个方程组,采用牛顿迭代法进行了求解。杨小龙[4]使用了一种牛顿迭代法的优化算法,通过构造迭代序列,完成了运动学正解求解,并将求解效率提高到0.3 ms。解析法通常采用消元方式消去约束方程中的未知数,从而获得方程解。通过解析解可以求得所有解,然而其推导过程十分复杂。Dietmaier[5]证明了一般 6-UPS 机器人有 40 个实数解。对于6-UPS机器人,Sreenivasan等[6]证明最多有 16 个解,当上、下平台是对称六边形时,Huang等[7]证明最多有 14 个解。为解决运动学正解解算问题,胡启国[8]、弓瑞[9]等采用遗传算法求得平台的位姿正解,该算法的解算精度较高,但其寻优解算用时较长。荆学东[10]、朱齐丹[11]等采用神经网络、牛顿迭代混合的算法完成了Stewart平台的正解,其迭代效率和解算误差均优于传统BP神经网络算法。
在进行六自由度运动平台设计时应避免奇异结构的出现,因此其包线内的运动学正解是唯一的。采用遗传算法、神经网络等先进算法进行运动学求解时需要进行大量的样本训练,很多时候也需要使用牛顿迭代法。六自由度运动平台的空间包线较小,非常适合采用牛顿迭代法进行运动学正解求解。改进的牛顿迭代法虽然效率较高,然而其构造过程复杂。本文将从简化运动学正解方程出发,结合六自由度运动平台的使用特点,通过选择合理的迭代初值完成位置正解的高效迭代寻优,同时利用解析法完成平台速度和加速度正解求解。
1 六自由度运动平台
一个典型的六自由度运动平台如图1所示,可以将其划分为上平台、下平台和支腿,其中下平台固定在地面上,支腿与上、下平台相交的位置为铰链点,同一平面上的铰链点位于同心圆上。
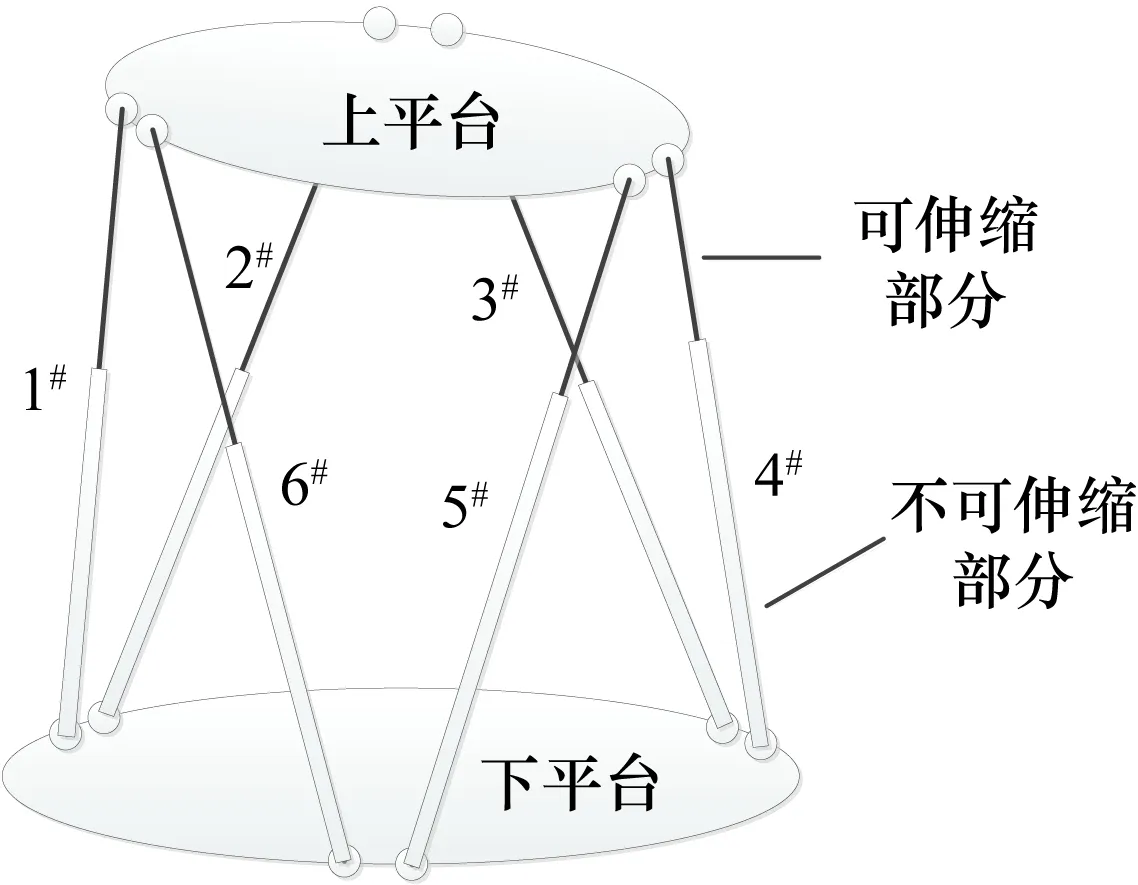
图1 六自由度运动平台结构图
支腿可以绕上、下铰链进行转动,并且支腿上部能进行伸缩运动。通过控制6条支腿的伸缩运动来实现对上平台的控制,从而为人在回路的仿真试验提供动感效应。
根据上、下平台圆半径、铰链间距和支腿长度即可确定平台的空间结构。平台铰链点的平面布局如图2所示,d1~d6为下铰链点,u1~u6为上铰链点,同一平面上的铰链点对称分布。
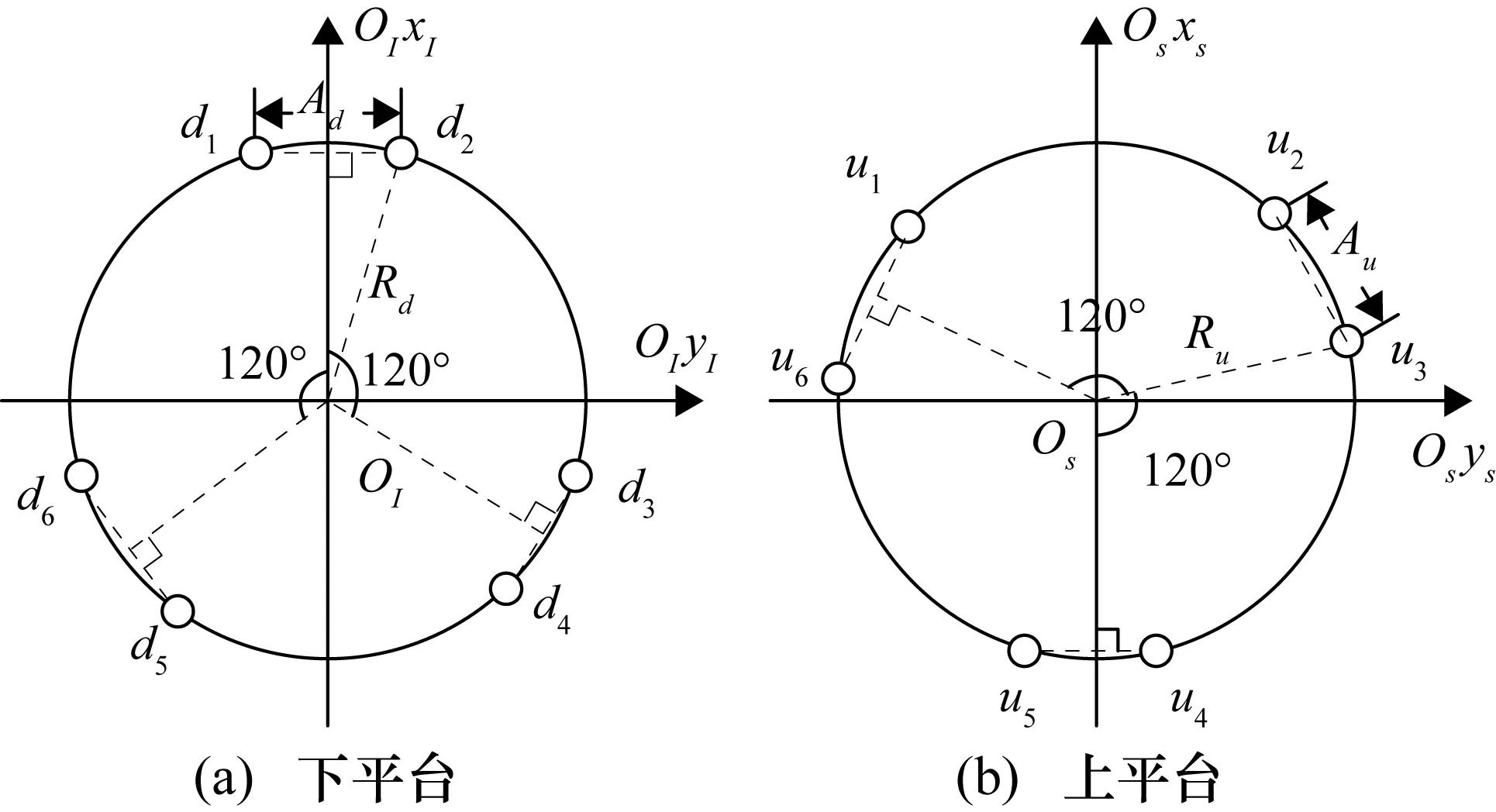
图2 运动平台铰链点平面分布图
2 坐标系定义
为了描述运动平台各节点组成部分在空间的运动学关系,需要建立统一的坐标系。
2.1 下平台坐标系
下平台坐标系(FI)坐标原点OI位于下铰链构成大圆的圆心,OIxI轴垂直于下平台d1、d2号铰链点的连线,OIyI垂直于OIxI指向右,并与OIxI在同一水平面内,如图2(a)所示。OIzI铅垂向下指向地心方向。
2.2 上平台坐标系
当支腿的长度相等且为某特定初始值Lt0时,即Lt1=Lt2=Lt3=Lt4=Lt5=Lt6=Lt0,上平台与下平台平行,并定义该位置为运动平台中立位。规定此时的上平台圆心Os为上平台坐标系(Fs)原点,纵轴Osxs垂直于上平台u4、u5号铰链点的连线,横轴垂直于Osxs指向右,如图2(b)所示。竖轴Oszs垂直于Osxsys平面,向下为正。上平台坐标系是一个可动坐标系,相对于下平台坐标系,除了坐标原点的平移运动外,还包括俯仰、滚转和偏航运动,其正方向定义与飞机欧拉角类似。
2.3 支腿坐标系
为了描述支腿向量与上平台、下平台之间的关系,需要建立支腿坐标系。下面以下平台d5铰链点所在的支腿坐标系为例进行说明:支腿惯性坐标系Fa的纵轴Oaxa轴平行于下平台相邻铰链点短边中垂线,正方向指向大圆圆心,横轴Oaya垂直于Oaxa轴,指向右侧,如图3所示。Oaza轴指向地心方向。

图3 支腿坐标系定义
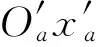
3 运动学关系
六自由度运动平台的上平台通过支腿与下平台相连,支腿坐标系相对于支腿惯性坐标系存在转动。建立支腿与上、下平台之间的运动学关系,需要利用点的复合运动理论进行分析。
3.1 点的复合运动
以任一支腿为例进行复合运动分析,已知该支腿伸缩速度和伸缩加速度分别为vr1和ar1,其方向沿支腿方向;支腿绕下铰链d1的角速度和角加速度分别为ωt1和αt1,其方向垂直于支腿矢量;支腿在惯性坐标系下的空间矢量为r1。

图4 支腿复合运动分析
根据速度合成定理,空间任一动点的绝对速度等于其牵连速度与相对速度的矢量和[12],则上铰链点u1相对于下铰链点d1的速度为
va1=ωt1×r1+vr1
(1)
式中:ωt1×r1垂直于支腿方向;vr1沿支腿方向。
支腿上铰链点相对于下铰链的牵连运动为定轴转动与平移运动之和,根据定轴转动加速度合成定理,则上铰链点u1相对于下铰链点d1的加速度为
aa1=αt1×r1+ωt1×ωt1×r1+ar1+2ωt1×vr1
(2)
式中:αt1×r1垂直于支腿方向;ωt1×ωt1×r1沿支腿方向,其大小为|ωt1|2·|r1|;ar1沿支腿方向;ωt1×vr1垂直于支腿方向。
3.2 运动学方程
根据平台结构参数,可以确定铰链点在相对应同心圆上的位置。假设6个下铰链点在FI坐标系下的位置为Pd,6个上铰链点在Fs坐标系下的位置为Pu,Pd和Pu均为3×6的矩阵。
上平台坐标系原点Os在下平台坐标系FI下的位置、速度和加速度分别为PI=[x;y;z],VI=[vxu;vyu;vzu]和AI=[axu;ayu;azu];上平台姿态角、角速度和角加速度分别为Euler=[θ;φ;ψ],ωs=[p;q;r]和αs=[dp;dq;dr]。
6个支腿在FI坐标系下的空间矢量为Pu2d,该矢量为3×6的矩阵。沿支腿方向的伸缩速度和伸缩加速度分别为vr和ar,均为6×1的矩阵。
根据上述定义,建立上平台位姿、速度和加速度与支腿位置、速度和加速度的运动学对应关系。
(1) 位置运动学关系。
根据上平台的姿态角,可以得到体轴系-地轴系转换矩阵Mbtg[13],该矩阵为3×3方阵。利用该转换矩阵可以将上平台上任一点转换到惯性坐标系。
根据空间矢量定义,可以建立运动平台位置对应关系:
Pu2d(:,i)=PI+Mbtg·Pu(:,i)-Pd(:,i),i=1,2,…,6
(3)
(2) 速度运动学关系。
假设上铰链点在FI坐标系下的速度为Vu,该矢量为3×6的矩阵,则
Vu(:,i)=VI+ωs×Pu(:,i),i=1,2,…,6
(4)
结合式(1)中点的复合速度分析,Vu沿支腿方向的映射速度即为支腿的伸缩速度:
|vri|=Vu(:,i)·Pu2d(:,i)/|Pu2d(:,i)|,i=1,2,…,6
(5)
(3) 加速度运动学关系。
假设上铰链点在FI坐标系下的加速度为Au,该矢量为3×6的矩阵,则
Au(:,i)=AI+ωs×ωs×Pu(:,i)+αs×Pu(:,i),i=1,2,…,6
(6)
上铰链点惯性系下的速度Vu沿垂直支腿方向的映射分量是由支腿的转动产生的。假设支腿的角速度为ωt,ωt为3×6矩阵,结合式(1)可求得:
ωt(:,i)=Vu(:,i)×Pu2d(:,i)/|Pu2d(:,i)|,i=1,2,…,6
(7)
再结合式(2),可求得支腿的伸缩加速度:
|ari|=Au(:,i)·Pu2d(:,i)/|Pu2d(:,i)|-|Pu2d(:,i)|·|ωt(:,i)|2,
i=1,2,…,6
(8)
至此,完成了上平台与支腿之间的运动学关系映射。
4 运动学正、逆解
六自由度运动平台的运动学正解是指根据支腿的位置、速度和加速度确定上平台的位姿、速度和加速度的过程;而运动学逆解则是由上平台的位姿、速度和加速度求解支腿的位置、速度和加速度的过程。可以将六自由度运动平台看作是并联结构机器人,其运动学方程具有逆解容易、正解难的特点。
4.1 运动学逆解
已知上平台的位置、姿态、速度、加速度、角速度和角加速度,基于式(3)、式(5)和式(8),可以直接求得支腿的位置、伸缩速度和伸缩加速度,即完成运动学逆解,这里不再赘述。
4.2 运动学正解
4.2.1 位置正解
位置正解需要解决的问题可以描述为:已知运动系统的结构参数,给定6个作动筒的长度Lt(i),i=1,2,…,6,求解上平台坐标系原点位置PI=[x;y;z]和姿态Euler=[θ;φ;ψ]。对运动系统进行位姿正解是一个求解高阶非线性方程组的过程[3]。
利用式(3),可得到以下方程组:
fi(x,y,z,θ,φ,ψ)=|PI+Mbtg·Pu(:,i)-Pd(:,i)|-Lt(i)=0,
i=1,2,…,6
(9)
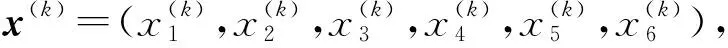
则有一阶泰勒展开式
可用矩阵表示为
0≈f(x(k))+J(x(k))(a-x(k))
解得:
a≈x(k)-J(x(k))-1f(x(k))
于是,就得到了牛顿迭代格式:
x(k+1)≈x(k)-J(x(k))-1f(x(k))
式中:J为雅可比矩阵。
当f(x(k+1))满足设定的误差要求时,则认为此时的x(k+1)为位置正解,即平台的位置和姿态。
4.2.2 速度正解
速度正解需要解决的问题可以描述为:已知运动系统的结构参数,给定6个作动筒的长度Lt(i)、伸缩速度|vri|,i=1,2,…,6,求解上平台速度VI=[vxu;vyu;vzu]。
利用式(4)和式(5),得到下面方程组:
gi(vxu,vyu,vzu)=(VI+ωs×Pu(:,i))·Pu2d(:,i)/
|Pu2d(:,i)|-|vri|=0,i=1,2,…,6
(10)
式(10)包含6个方程式,利用广义拟求解方法可以求得上平台的速度VI=[vxu;vyu;vzu]。
4.2.3 加速度正解
加速度正解需要解决的问题可以描述为:已知运动系统的结构参数,给定6个作动筒的长度Lt(i)、伸缩速度|vri|、伸缩加速度|ari|,i=1,2,…,6,求解上平台加速度AI=[axu;ayu;azu]。
利用式(6)~式(10),得到下面方程组:
hi(axu,ayu,azu)=Au(:,i)·Pu2d(:,i)/|Pu2d(:,i)|-
|Pu2d(:,i)|·|ωt(:,i)|2-|ari|=0,i=1,2,…,6
(11)
式(11)包含6个方程式,利用广义拟求解方法可以求得上平台加速度AI=[axu;ayu;azu]。
4.3 运动学解算流程图
六自由度运动平台的运动学解算过程如图5所示。根据平台的结构参数和上平台目标运动参数,经运动学逆解得到支腿的位置、速度和加速度;利用运动学正解方程完成平台位姿、速度和加速度的正解。
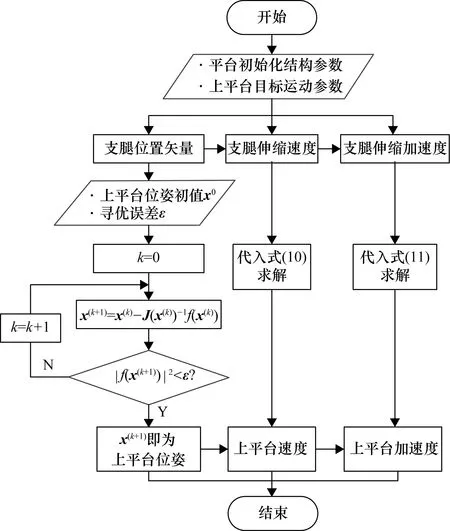
图5 六自由度运动平台运动学解算流程图
5 仿真结果与分析
以某运动平台结构参数为例,对六自由度运动平台的运动学关系进行仿真建模和验证。该运动平台结构参数如表1所示。

表1 某运动平台结构参数列表 单位:mm
仿真模型结构如图6所示。模型由运动学逆解模块、作动系统、运动学正解模块3个部分组成,模块之间的关系如下。

图6 六自由度运动平台运动学模型结构图
① 运动学逆解模块的输入为平台的目标位置、速度、加速度、欧拉角、角速度和角加速度指令,经运动学逆解解算后,得到支腿的作动指令。
② 作动系统根据作动指令驱动支腿运动,并可以通过电机编码器得到支腿的实际位置、速度和加速度。
③ 将支腿运动状态输入运动学正解模块,解算得到平台的实际运动状态。
为了验证平台的运动学关系,这里假设作动系统为无延迟的理想环节,则平台目标运动指令值应与运动学正解模块解算得到的平台状态一致。
5.1 模型解算性能分析
运动学模型中的运动学逆解模块可以看作线性定常系统,其解算速度很快。又因为速度和加速度正解方程也是线性的,因此重点对运动学位姿正解解算过程进行分析。
选择3个不同的支腿长度状态作为运动学正解模块输入,以平台位于中立位作为迭代寻优初值,寻优过程如表2所示。其中状态点1=[4795;4795;4795;3295;3295;3295],状态点2=[3300;3581;4158;4521;3854;4029],状态点3= [3500;4795;4500;3600;3800;4300]。

表2 运动学正解迭代寻优过程
由表2可知,对于不同的支腿状态,经5次迭代寻优后,即可得到上平台的位姿参数。寻优耗时不超过2 ms,均方差小于1,完全满足工程应用实时性要求。
将迭代过程的均方差用图形表示出来,如图7所示,可以更好地展示寻优收敛速度。事实上,经过4次迭代后的解算精度已经很高。

图7 寻优结果均方差随迭代次数增加变化图
采用牛顿迭代法进行位姿正解求解,不同的迭代初值会影响模型的解算效率。下面将通过选择不同的迭代初值对迭代结果和效率进行分析。
假定迭代初值为上平台圆心在下平台坐标系下的位姿,寻优初值1=x(0)=(0,0,3000,0°,0°,0°)位于下平台以下,即不在运动平台包线范围内。寻优初值2=x(0)=(0,0,-6000,0°,0°,0°)位于下平台之上,同样超过系统的包线范围。寻优初值3=x(0)=(0,0,-3147,0°,0°,0°)是平台位于中立位时的上平台位姿参数。针对状态点1~状态点3,采用不同的迭代初值进行解算,寻优结果如表3所示。

表3 不同迭代初值的寻优结果
由表3可知,不合理的初值设定(例如初值1),会导致寻优结果不在运动系统包线范围内;而将初值设定在下平台之上的两个状态点,寻优结果合理且唯一,初值与寻优结果较近的状态点寻优时间略短,总体寻优时间均不超过2 ms。
考虑飞行模拟器六自由度运动平台的工作特点:平台每次均从中立位开始运动,在洗出算法影响下选择“初值3”,即平台中立位的位姿作为迭代初值,原因如下:① 运动平台的初始运动均从中立位开始;② 每完成一次突发运动,在洗出算法的影响下平台会“悄悄”回到中立位[14-15]。因此,选择中立位的位姿作为迭代初值可以最大限度地减少寻优时间。
5.2 运动包线解算
在进行运动平台包线计算时,将6个支腿由最短到最长进行遍历,由此求得上平台的最大空间状态即为平台的运动包线。以单个支腿取100个特征点为例,则完成支腿的遍历需要进行1006次计算。假设单次计算耗时1 ms,完成包线计算时间需要超过26万小时。
笔者提出一种计算运动平台包线的可行方案,即每个支腿只选择最长、最短2个状态进行遍历,经过26=64次计算,即可完成运动包线解算。
表4中的L为0代表最短支腿长度,1代表最长支腿长度。完成表4中运动系统的包线解算仅用时55 ms。由计算结果可知,本文建模所用的六自由度运动平台纵向运动范围为±1.5 m,侧向运动范围为±1.6 m,垂向运动范围为±0.9 m。平台的空间包线是其重要性能指标,一定程度上决定了平台的运动能力。

表4 六自由度运动平台空间包线
5.3 复合运动分析
选取一组正弦波复合运动数据作为上平台指令值输入,经运动学逆解模块解算后,得到6个支腿的作动指令,经作动系统后驱动上平台运动。将上平台的指令值与运动学正解模块输出值进行对比,如图8~图10所示。
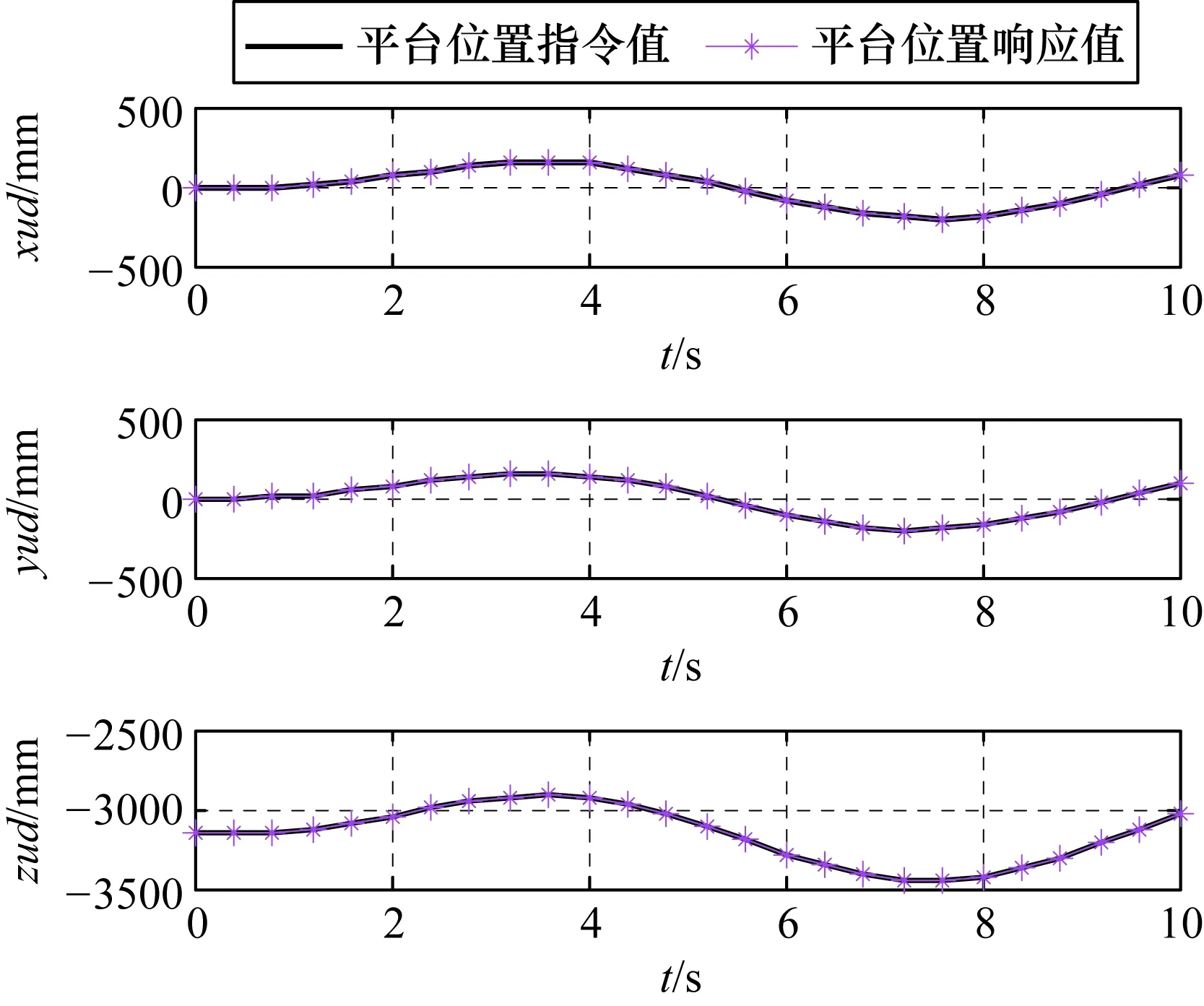
图8 平台位置指令与响应值对比
由图9和图10可知,平台的指令值与响应值完全一致,证明了所建立的六自由度运动平台运动学关系正确。当然,对于实际作动系统,平台指令值与响应值之间将存在一定的延迟与偏差。

图9 平台速度指令与响应值对比
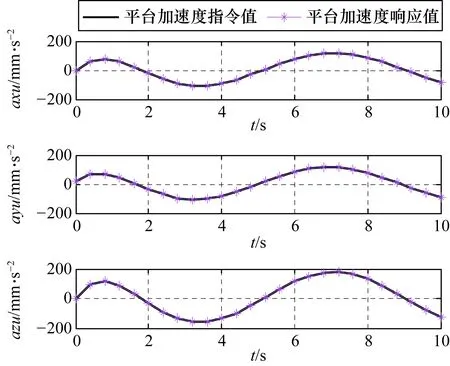
图10 平台加速度指令与响应值对比
6 结论
通过引入点的复合运动理论,建立了平台与支腿之间的位置、速度、加速度运动学关系。利用MATLAB/Simulink环境搭建了运动学模型,并设计了合理的验证方法。仿真结果表明,所建立的运动学模型具有解算速度快、准确度高等特点,可满足工程实时解算需求。本文的创新点和贡献如下:
① 针对六自由度运动平台的非奇异结构特点,选择牛顿迭代法完成运动学位置正解求解;提出了一种合理的初值选择方法,并证明了合理区域内即使初值与寻优结果差异较大,也可以完成算法的快速收敛。
② 分析指出采用遍历的方法求得运动系统的包线非常困难,给出了一种可行的运动包线寻找方法,通过6个支腿的状态组合完成了运动平台空间包线的计算。
③ 在完成位置正解的基础上,创新性地引入点的复合运动理论,利用解析的方法完成了六自由度运动系统速度和加速度正解,为作动系统伺服电机控制引入了更多的控制参数,有助于提高控制精度。
