基于SVDD和PF的剩余使用寿命预测方法研究

焦瑞华， 马 欣， 李晓猛， 董智超

(航空工业西安航空制动科技有限公司，陕西 西安 710048)

随着对复杂工程系统运行的可靠性和安全性的需求不断增加，使得相应的维修策略逐步从传统的事后维修和定期维修向视情维修转变。而故障预测与健康管理(Prognostics and Health Management，PHM)技术能够通过预测失效的发生来降低系统风险以实现系统的视情维修，因此在近些年得到越来越多的关注、研究与应用，已经成为可靠性领域的热点研究方向。而剩余使用寿命(Remaining Useful Life，RUL)的预测是PHM技术中最具挑战性的核心技术问题，其一般是指系统在当前状态下还能有效运行直到生命终止的时长[1]，能够为后勤保障人员提供系统失效前安全运行的时间信息，从而有针对性地制定维护与维修方案。因此，精准的RUL预测对于提升系统的可靠性与安全性无疑有着非常重要的意义。

近年来，RUL预测技术发展迅猛并取得了大量的优秀成果。现有的预测方法通常可以分为三大类：基于模型的方法、数据驱动的方法和混合模型方法。基于模型的方法的基本思想是建立一个能够描述系统物理特性和失效模式的数学模型，从而实现RUL的预测，它一般可以获得较为精确的预测结果，但不能应用于缺乏物理退化先验知识的系统，例如经典的Paris-Erdogan 模型[2]，其经常用于轴承、齿轮等的疲劳裂纹扩展的预测。数据驱动的方法能够基于大量的历史数据构建输入和输出之间的映射关系来预测RUL，从而避免了基于模型方法的缺点，其一般又可以分为基于可靠性模型、基于随机过程和基于人工智能的方法[3]。基于可靠性模型的方法是从过去故障历史数据的统计特性角度进行故障预测，其中研究最多、应用最广的方法就是比例风险模型[4]；基于随机过程的方法是指利用数理统计和随机过程的相关知识建立随机过程模型来描述退化轨迹，以得到概率框架下的剩余寿命概率分布，其中研究与应用最多的是Wiener模型[5]；基于人工智能的方法往往是利用支持向量机[6]、人工神经网络[7]和循环神经网络[8]等深度学习模型来对历史数据进行训练，使其满足一定精度要求后再进行故障预测。混合模型的方法通常是前述几种方法的有效结合，可以充分发挥不同模型的长处并克服单种类方法的局限性，因此，近年来受到大量学者的关注和研究。Acar等[9]构建了一个加权求和公式，将基于高斯过程、支持向量机和径向基网络等5种方法的结果进行加权求和来减小预测结果的误差；Wei等[10]提出了一种结合支持向量机和粒子滤波算法的框架来进行电池的RUL预测。实验结果表明该方法提高了预测结果的准确性。然而，如何开发一个可靠且有效的混合模型仍然是一个难点。

一般而言，RUL的预测往往是基于大量的测量数据来实现的，而如何从海量的具有过程噪声的连续采集的监测数据中提取退化特征来监测系统的性能退化趋势，进而精准地预测出RUL是一个挑战。支持向量描述(Support Vector Data Description，SVDD)最早由Tax和Duin[11]提出，是一种用于离群点检测和分类的模型，其一直以来被用于故障诊断的研究。然而考虑到SVDD可以用于检测待测样本到SVDD超球面的距离，因此可以用监测数据到故障数据集距离的不断减小来表征系统健康指标的逐步退化。粒子滤波(Particle Filter，PF)为一种基于贝叶斯估计的非线性滤波算法[12]，为了实现RUL可靠预测的同时提供一个大概率的故障时间范围，PF算法经常被用于RUL预测的研究。例如，Liu等[13]提出了一种基于PF的粒子学习框架来预测锂离子电池的RUL；Qian等[14]提出了一种改进粒子滤波方法，并将其应用于滚动轴承的RUL预测中。实验结果证明了这种方法的优越性。

基于上述分析，笔者提出了一种基于SVDD和PF的退化趋势监测和RUL预测的框架。首先，基于历史故障数据建立SVDD模型来构建健康指标以监测系统的退化；然后，建立一个可以描述健康指标退化趋势的退化模型；最后，基于PF算法和自动确定的故障阈值来实现RUL的预测。所提出的方法主要具有以下优点：利用SVDD构建健康指标无须专家的先验知识，具有同通用性；故障阈值设定方法避免了传统手工指定故障阈值而可能导致的预测误差，提升了预测结果的准确性；基于SVDD和PF的预测框架能够监测系统的退化趋势并提供准确可靠的RUL预测结果。

1 基本理论

1.1 支持向量描述

SVDD的主要思想是在高维空间中找到要描述的目标数据集周围的球形边界，在考虑到异常值存在的条件下，要包含尽可能多的目标数据[15]。 SVDD的算法原理如图1所示，在三维特征空间中存在一个类别为“1”的目标数据集，定义一个球心为a、半径为R的超球模型，则SVDD模型训练的目的是通过最小化R来找到体积最小的超球体，以对目标数据进行准确的描述，使被描述的数据尽可能多地被包含在超球体内，而其中用于边界描述的数据就被称为支持向量。

图1 SVDD算法原理

给定一个训练数据集xi∈Rd,i=1,…,N，假设存在中心为a、半径为R的超球模型，则SVDD的优化问题就转变为

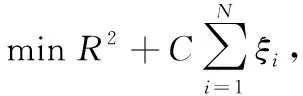
(1)

式中：ξi为引入的松弛因子，目的是防止过拟合；C为用户定义的固定参数；φ(xi)为能够将训练数据xi映射到高维空间的函数。那么上述问题可以通过最优化下面的对偶问题得到解决。

(2)

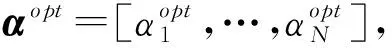
(3)

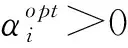
(4)

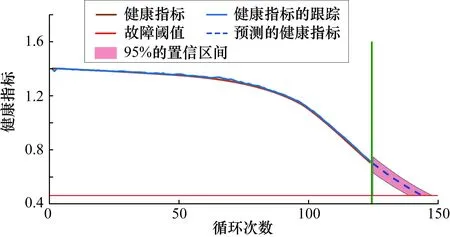
如果D>R，则测试样本被视为离群值，即不属于目标样本这一类；如果D

1.2 粒子滤波

PF的主要思想是基于蒙特卡罗方法利用重要性密度函数对大量随机粒子进行采样，并赋予每个粒子一个重要的权重来表示后验概率密度[16]。假设一个动态系统可以表示为如下的状态空间模型：

(5)

式中：xk为k时刻系统的状态；zk为k时刻xk的测量值；wk-1和vk分别为k-1时刻和k时刻的过程噪声和测量噪声。PF的核心问题是如何构造后验滤波分布p(xk|z0:k)，一般分为预测和更新两个步骤。在预测阶段，k-1时刻的后验概率p(xk-1|z0:k-1)是已知的，则先验概率p(xk|z0:k-1)可以通过式(6)得到。

(6)

然后，当测量到k时刻的zk时，对后验概率进行更新：

(7)

式(6)和式(7)的运算依次重复，形成递归贝叶斯估计。然后采用蒙特卡罗采样从后验概率分别采集带权重的粒子集样本集，用粒子集表示后验分布，将积分转换为求和形式。具体来说，就是后验分布通过粒子集近似为经验估计，可用如下的估计来实现近似：

(8)

2 基于SVDD和PF的RUL预测

2.1 基于SVDD的健康指标构建

直接利用复杂系统的大量监测数据来识别系统的健康状态往往是行不通的。为了识别复杂系统的健康状态，提出了一种基于SVDD的健康指标构建方法，其核心思想是利用SVDD对故障数据集进行描述，而随着系统运行时间的推移，健康状态逐渐劣化最终会退化到故障状态，从而使测试样本到SVDD超球面的距离逐渐减小并最终小于SVDD的球半径。假设采集的系统的故障数据集可以表示为

(9)

式中:n为测量变量的个数;m为测量次数。然后，基于故障相关的数据集建立相应的SVDD模型，则可通过式(10)来计算超球面的半径。

(10)

在线监测时，一旦获得新的时刻t的测量值，可由式(4)得到当前监测样本到故障超球面中心的距离，则可以定义如下健康指标:

(11)

2.2 基于健康指标退化模型和PF的RUL预测

为了提供一个高概率的可能发生故障的时间范围，利用PF算法与本文提出的自适应故障阈值来预测RUL。首先，针对健康指标的退化趋势拟合一个退化模型，并构建退化模型参数相关的状态空间方程。

(12)

式中：θk为预测模型的参数；HIk为拟合的健康指标。所有的噪声都认为是服从高斯分布的。g(θk,k)是用于拟合的退化模型，它可以有多种不同的形式以满足不同对象的需求，例如：自回归滑动平均模型、灰色模型等时间序列模型、多项式模型、指数模型、神经网络模型等。而考虑到所使用对象的潜在特征形式是指数型的[17]，此处选用具有良好拟合效果的双指数模型。一般来说，选择退化模型的主要依据一方面是通过数据的初步分析，了解数据的特点之后选择合适的模型；另一方面是可以选择几种模型进行实验，基于实验结果选择精度最高的模型。

基于模型(12)，引入PF算法来估计退化模型参数θk的概率密度函数。假设HI1:k表示时间序列(1:k)对应的健康指标的观测值，则健康指标的p步预测的过程如下。

② 粒子更新。基于式(7)和前一时刻的粒子集计算当前k时刻的粒子权重：

(13)

④ 状态估计。利用新的粒子和权重估计新的预测模型参数。

(14)

⑤ 健康指标预测。基于式(8)可以得出k步超前预测的概率密度函数p(θt+k|z0:t)，从而可按式(15)计算预测模型参数的p步预测。

(15)

最终就可以通过式(12)所示模型推导出健康指标的p步预测。

(16)

在进行RUL预测时，故障阈值的选取同样非常重要。一般都是根据经验或者专家知识指定一个故障阈值，而提出的故障阈值设定方法无须专家知识，可将其定义为

FT=ζRf

(17)

(18)

同时进一步可以按照式(19)估计预测的RUL的概率密度函数。

(19)

综上所述，提出的基于SVDD和PF的RUL预测框架详细的流程如图2所示。

图2 基于SVDD和PF的RUL预测流程图

3 实验验证

3.1 航空发动机退化数据集

所用航空发动机退化数据集是由商业软件C-MAPSS[18]生成的多组全寿命仿真退化数据，已经被广泛地应用于RUL预测的研究中。实验方法为对发动机多次循环运行时的数据进行记录，形成4个数据集，每一组数据集记录了100台航空发动机的退化监测数据。但每一台发动机的初始磨损程度是不同的。此外，发生故障的精确时间、噪声的大小和准确的初始磨损量值对研究者来说也是未知的。

3.2 实验结果

选用单一工况和单一故障的FD001数据集进行实验验证，虽然共包括了21个监测数据，然而其中有一些监测数据是恒值，并不能为RUL的预测提供任何有用信息。因此，选择序号为2，3，4，7，8，9，11，12，13，14，15，17，20，21的14个监测数据作为输入数据。又由于监测数据伴有噪声污染，因此选用最小二乘滤波(窗口长度设置为30)去除噪声的影响。为了消除不同监测数据量纲的影响，利用零均值标准化方法对监测数据进行归一化。SVDD选用高斯核函数，权衡参数C设置为0.02。此外，与故障阈值相关的参数设置为ζ=0.9，则故障阈值可按照式(17)计算得到FT=0.4626。实验得到的100台发动机的健康指标如图3所示。

图3 100台发动机的健康指标

由图3可知，100台发动机的初始退化有所差异，这符合数据集每一个发动机拥有不同的初始磨损程度的特点。而随着运行时间的不断增加，健康指标逐步减小，这表明所构建的健康指标可以反映发动机健康状况的逐步退化。

随机选取第40台和第58台发动机为例进行分析。首先对第40台发动机运行到159次循环时进行RUL的预测和分析，实验结果如图4所示。绿线为预测开始的时间点，退化特征预测的均值用蓝线表示，95%置信区间用粉红色区域表示。根据图4在159次循环时预测的健康指标的发展趋势，即利用前159次循环的数据来更新健康指标退化模型。然后利用外推健康指标直到达到故障阈值为止，以此计算出发动机的寿命终止时间，可以看出估计的发动机寿命终止时间的中位值和95%置信区间分别为178次循环和[165，190]。而真实的终止时间是188次循环，误差为10，落入了预测的置信区间之内。

图4 第40台发动机在159次循环时的预测结果

由于使用的贝叶斯方法具有统计特性，RUL的预测结果是由2000个粒子来近似分布的。在得到发动机的寿命终止时间之后，根据式(18)和式(19)分别计算RUL和其95%置信区间，可以得到RUL预测的中位值和95%CI分别为19个循环和[6，31]，而真实的剩余寿命是29个循环，误差为10，具体的概率密度函数如图5所示。

图5 第40台发动机RUL的概率密度函数

第58台发动机的预测结果如图6所示，利用前124次循环的数据来更新健康指标退化模型。然后利用外推健康指标直到达到故障阈值为止，以此计算出发动机的寿命终止时间，可以看出估计的发动机寿命终止时间的中位值和95%置信区间分别为144次循环和[139，148]。而真实的终止时间是147次循环，预测误差为3。

图6 第58台发动机在124次循环时的预测结果

同样根据式(18)和式(19)分别计算RUL和其95%置信区间，可以得到RUL预测的中位值和95%CI分别为20个循环和[15，24]，而真实的剩余寿命是23个循环，具体的概率密度函数如图7所示。从图7中可以看出所预测的RUL和真实的RUL非常接近，同样证明了所提出方法的有效性。

图7 第58台发动机RUL的概率密度函数

使用的C-MAPSS数据集已广泛用于RUL预测的研究中，采用常用的均方根误差(RMSE)、平均绝对误差(MAE)和准确度(Acc)进行评价。将所提出方法与一些已有的研究方法进行比较，精确度的计算方法为

(20)

为了说明所提出方法在RUL预测方面的优越性，选择基于案例分析(IBL)、支持向量机(SVM)、长短期记忆网络(LSTM)和卷积神经网络(CNN)的方法作为对比方法。表1列出了这些方法与所提出方法的详细的对比结果，其中NA表示原文中没有应用这项评价指标。综合来看，本文提出的方法取得了不错的预测性能。此外，所提出的方法无须大量的计算时间和计算资源，还可以提供一个高概率的失效时间范围而不仅仅是RUL这一单一数值，可以为系统的视情维修提供重要的参考。

表1 多种方法对比结果

4 结束语

针对复杂系统的健康状态监测和RUL预测的问题，提出了一个基于SVDD和PF的RUL预测框架。通过对航空发动机退化数据集进行案例分析，实验结果表明所提出的基于SVDD的健康指标构建方法能够提取可以表征系统健康状态退化的健康指标，基于PF算法和所提出的自动故障阈值设定方法能够准确地预测出发动机的RUL。此外，通过与现有方法的对比分析发现，提出的RUL预测框架不仅具有较高的预测精度，同时还可以提供一个可能的实效时间范围来为维修决策提供更多的有用信息，具有广阔的应用前景。