基于堆积试验的黑水虻离散元仿真参数标定与分析

彭才望，周 婷，孙松林，谢烨林，魏 源

(湖南农业大学 机电工程学院，湖南 长沙 410128)

近年来，随着规模化养猪场的迅速发展，猪场的粪污排放量逐渐增多，对猪场周围的大气、地下水等造成了严重的环境污染。同时，给人体的生活健康带来一定的危害。黑水虻幼虫(黑水虻)在畜禽粪便“肥料化利用”过程中作用明显，能实现减污、资源循环利用。近年来针对黑水虻的研究主要集中在黑水虻对畜禽粪便和餐厨垃圾的转化率、黑水虻幼虫营养成分、黑水虻自身生长参数变化等方面。而黑水虻处理畜禽粪便后续分离环节中筛分机械应用程度低，分离效率低、成本高，降低了规模化生产率。

黑水虻分离是指在黑水虻幼虫养殖成熟后期，通过一定工程技术方法将畜禽粪便等养殖基料中的黑水虻排泄物、分泌物以及养殖基料残渣分离，获得黑水虻产品，是黑水虻处理畜禽粪便实现资源化利用的关键环节之一。黑水虻的物性参数与接触参数是实现机械化分离黑水虻的关键之一。堆积角作为散体物料的固有属性，常被用作散体物料颗粒参数标定，也可用来研究散体颗粒的复杂力学特性。离散元法可以模拟颗粒间微观与宏观变形，在农业机械、农业物料领域得到广泛的应用。王国强等阐述了通过离散元堆积角试验与实际试验值对比验证，获取离散元参数。林嘉聪等通过堆积角试验与离散元仿真堆积角虚拟试验相结合的方法，量化了蚯蚓粪的滚动摩擦因数。徐莉等对蝇蛆与固体畜禽粪便混合物分离运动进行了离散元仿真研究，量化了蝇蛆的物性参数与接触参数并揭示了蝇蛆与振动筛模型间的运动学规律，为同属于资源性昆虫的黑水虻仿真研究提供了借鉴依据。但是，黑水虻与蝇蛆在生物特性与形态方面存在一定差异，目前应用离散元方法对黑水虻仿真模型的研究鲜有报道。

本文以黑水虻幼虫为研究对象，分析黑水虻的生物特性，利用EDEM仿真软件并选取系统中的“Hertz-Mindlin with JKR”接触模型，进行堆积角仿真试验。首先，应用Plackett-Burman设计试验筛选对黑水虻堆积角影响显著的参数。然后，进一步以堆积角作为响应值，通过三因素二次回归正交旋转组合响应面试验确定出最优参数组合，并将标定后的最优参数进行仿真，对比验证堆积角以确定出黑水虻的组合参数。以期为机械分离黑水虻的离散元仿真模拟提供基本参数，并为黑水虻在虫沙分离环节中的瞬间运动状态研究奠定基础。

1 材料与方法

1.1 基本参数

试验采用湖南大湘农环境科技股份有限公司提供的黑水虻样品，该黑水虻是8日龄黑水虻幼虫投放到含水率70%～80%的新鲜猪粪中养殖8 d后，且在化蛹前的状态，黑水虻取食猪粪中营养物质获得生长并进行生物转化。试验时，因生物应激性使黑水虻的外形容易发生变化，形成伸直(外形自然伸展)与蜷曲(外形受应激而萎缩)两种状态的体型，导致与仿真试验结果存在一定的差异。因此，为得到堆积试验自然状态的黑水虻，堆积试验结束瞬间，喷洒化学试剂使黑水虻保持瞬间不变状态，克服非物性接触参数带来的不利影响。然后，每次随机选取预蛹前的50条黑水虻幼虫，重复试验，测得伸直状态黑水虻体长23.3 mm，标准差0.70 mm，蜷曲状态黑水虻体长19.4 mm，标准差0.58 mm；虫宽4.9 mm，标准差0.34 mm；虫体重为0.177 g。伸展状态和蜷曲状态的黑水虻数量分布比例为3∶2，黑水虻如图1所示。

1.2 黑水虻堆积物理试验

黑水虻堆积角通过箱体抽板法试验测得。测量装置(不锈钢材料)由箱体(长100 mm、宽100 mm、高150 mm)、挡板(长100 mm、高150 mm)和底板(长200 mm、宽200 mm)组成。试验时将黑水虻置于箱体中，缓慢向上抽提挡板，设定挡板向上抽提速度为50 mm·s，失去挡板壁面的支撑后，黑水虻滑出箱体，因黑水虻自身具备生物应激性，堆积落地后，黑水虻自身外表产生非自身接触参数导致的微观变化，影响堆积角真实测量。因此，堆积稳定瞬间利用高速摄影机在垂直钢板底平面的方向连续拍照，堆积的坡面与底板的水平面形成的夹角即为堆积角。选取黑水虻自然堆积形态较稳定、应激性干扰小的图像导入CAD软件中进行堆积角标注。为降低生物应激性带来的误差并较真实反映黑水虻堆积过程中的自然状态，换用新的黑水虻样品重复试验5次，取其堆积角平均值34.66°，标准差为0.65°，如图2所示。

图1 黑水虻幼虫Fig.1 Black soldier fly larva

2 仿真模型

2.1 黑水虻仿真模型

依据文献[21，23-25]，将黑水虻颗粒间的接触设定为软球模型，颗粒接触形式如图3所示。颗粒间的接触方式简化为弹簧阻尼系统，接触模型简化如图4所示。试验过程中颗粒间所发生的碰撞力简化为软球模型间的接触合力，通过牛顿运动定律对、颗粒间的运动与相互作用进行计算。接触合力可分解为颗粒与颗粒碰撞时的接触法向力与接触切向力。软球模型之间的合力计算公式为：

=∑(+)。

(1)

式中—颗粒和间的接触合力(N)；—颗粒和间的接触法向力(N)；—颗粒和间的接触切向力(N)。

黑水虻颗粒模型在堆积碰撞运动试验中，可将发生的碰撞设定为颗粒和之间的碰撞，颗粒从图3虚线位置运动到实线位置，运动形式包括法向运动、切向运动以及颗粒间的滚动运动，不考虑颗粒和之间的自身变形，、分别为颗粒间碰撞接触时重叠处的位移量和切向位移。根据黑水虻颗粒软球模型及其受力与运动分析情况以及黑水虻处理畜禽粪便过程中养殖基料中存在一定的湿度，黑水虻表面存在一定的黏性，依据文献[21]，在EDEM软件中应用Hertz-Mindlin with JKR模型进行黑水虻堆积角仿真试验。

1，底板；2，黑水虻幼虫；3，挡板；4，箱体；5，底座板。1， Bottom plate; 2， Black soldier fly larva; 3， Baffle; 4， Box; 5， Base plate.图2 箱体抽板法试验Fig.2 Test of box side plate lifting method

图3 颗粒接触形式Fig.3 Form of particle contact

黑水虻因自身生物特性导致体长变化，呈现伸展与蜷曲两种状态。为建立合乎实际的黑水虻模型，在不影响分析结果的前提下，按照图4测得黑水虻的基本参数，采用16个球颗粒两两重叠组合的方式，通过调整圆球坐标位置，使各个圆球球心均在同一水平面上，建立黑水虻的仿真模型如图5所示。

2.2 仿真参数设置

EDEM仿真试验需要设置黑水虻颗粒与边界相关参数。其中边界为不锈钢材料，参数唯一确定。黑水虻颗粒因自身生物特性，实际物理试验测量比较困难，离散元参数值难以确定唯一性，且当前缺乏黑水虻离散元仿真与试验研究相关的文献。因此，结合文献[23-25]中蝇蛆与蛆料振动筛分离散元仿真参数，确定了本研究中各仿真参数的变化范围如表1所示。

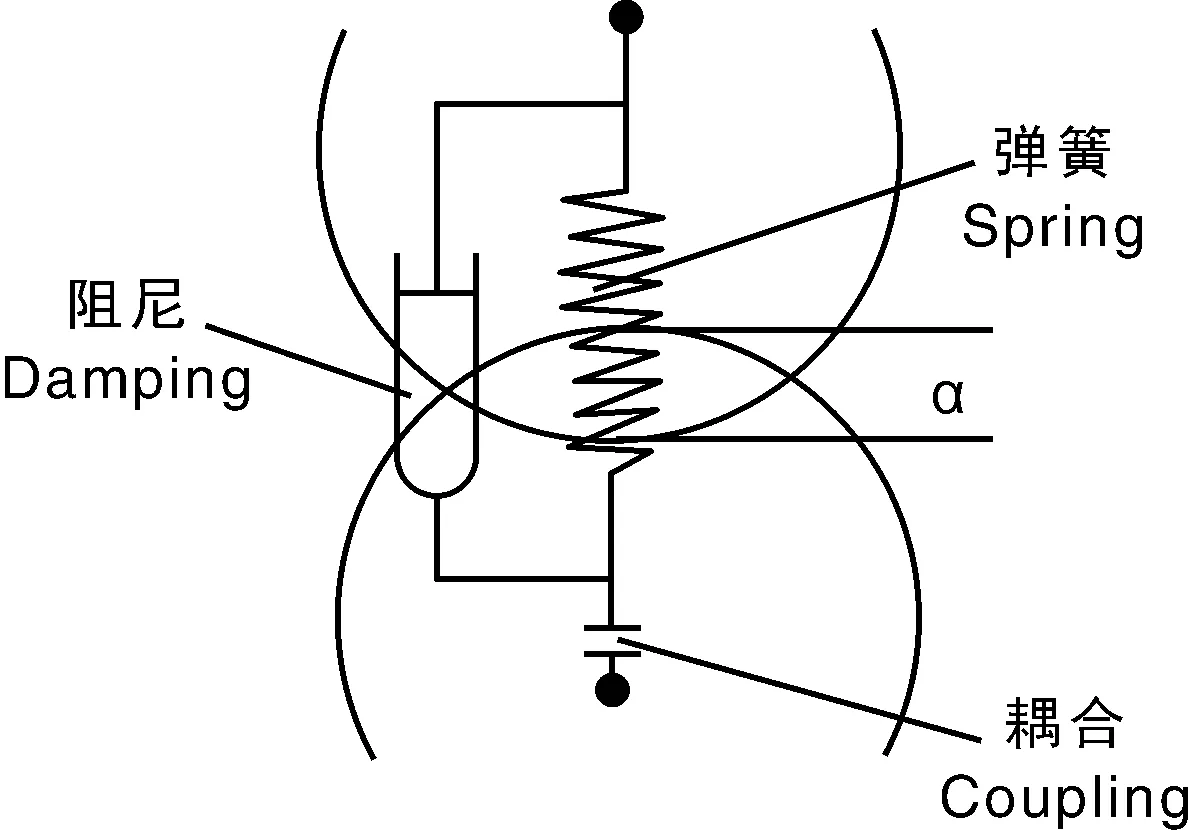
图4 颗粒接触模型简化Fig.4 Model of particle contact

图5 黑水虻仿真模型Fig.5 Simulation model of black soldier fly

2.3 试验模型

在EDEM软件中导入与箱体抽板法物理试验尺寸相同的箱体模型(长100 mm、宽100 mm、高150 mm)，箱体底部添加与箱体垂直的水平面底板(长200 mm、宽200 mm)，如图6所示。箱体顶部设置一个虚拟平面作为颗粒工厂，颗粒生成的速度为0.20 kg·s，生成时间为2.50 s，黑水虻颗粒总质量0.5 kg，将伸直与蜷曲两种状态的黑水虻颗粒模型按数量分布设置3∶2，以动态随机方式生成并落入箱体内部。在Simulator中，瑞利时间步长设置为22%，仿真中网格尺寸取2倍最小球形单元尺寸。为了保证黑水虻颗粒快速稳定，设定颗粒初始下落速度为0.5 m·s，待黑水虻颗粒充满箱体且颗粒群稳定后，挡板垂直向上以50 mm·s的速度提升，失去挡板壁面的支撑，颗粒群滑出箱体并从底部逐渐流出，待黑水虻颗粒群稳定后，其坡面与底平面所形成的夹角即为黑水虻堆积角，后处理中在垂直颗粒堆坡面方向截取图像并导入CAD软件中进行堆积角标注。

表1 仿真参数设置

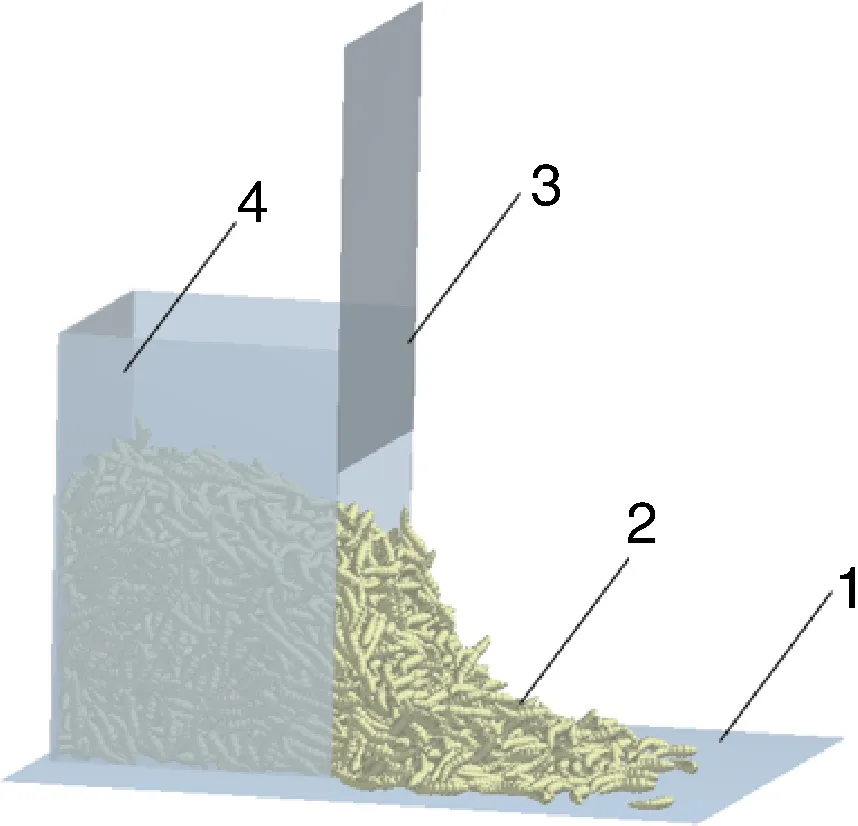
1，底板；2，黑水虻；3，挡板；4，箱体。1， Bottom plate; 2， Black soldier fly larva; 3， Baffle; 4， Box.图6 箱体抽板法堆积角仿真Fig.6 Simulation of box side plate lifting method

3 仿真试验

3.1 试验设计

应用Design-Expert软件进行Plackett-Burman(PB)试验设计，筛选对黑水虻堆积角影响显著的参数。根据EDEM仿真时用到涉及黑水虻颗粒相关的参数，选取表1中影响黑水虻堆积角的10个参数变量作为试验因素，并预留1个虚拟变量()用作误差分析。根据表1给定的参数建立黑水虻颗粒模型开展堆积角仿真试验，其中～分别选择上限、下限两个数值作为高、低2个水平(1、-1)，试验中设3 个中心点，根据未知参数数量进行15次试验。应用Design-Expert软件进行PB试验设计及结果如表2所示，其中～为因素水平值，为空白列。

对表2所示的Plackett-Burman试验结果进行分析，得到10个因素对黑水虻堆积角贡献率如表3所示。由表3可知，10个因素中对黑水虻堆积角影响较为显著(<0.05)的3个因素依次为：(黑水虻间静摩擦系数)、(黑水虻间滚动摩擦系数)、(黑水虻剪切模量)，且这3个因素对堆积角均为正效应，即堆积角随着该3个因素增大而增大。其余因素影响不显著(>0.05)。因此，在后续最陡爬坡试验和二次回归正交旋转组合响应面试验中选取这3个参数作为试验因素进一步分析，其余非显著性参数选取中间水平值。

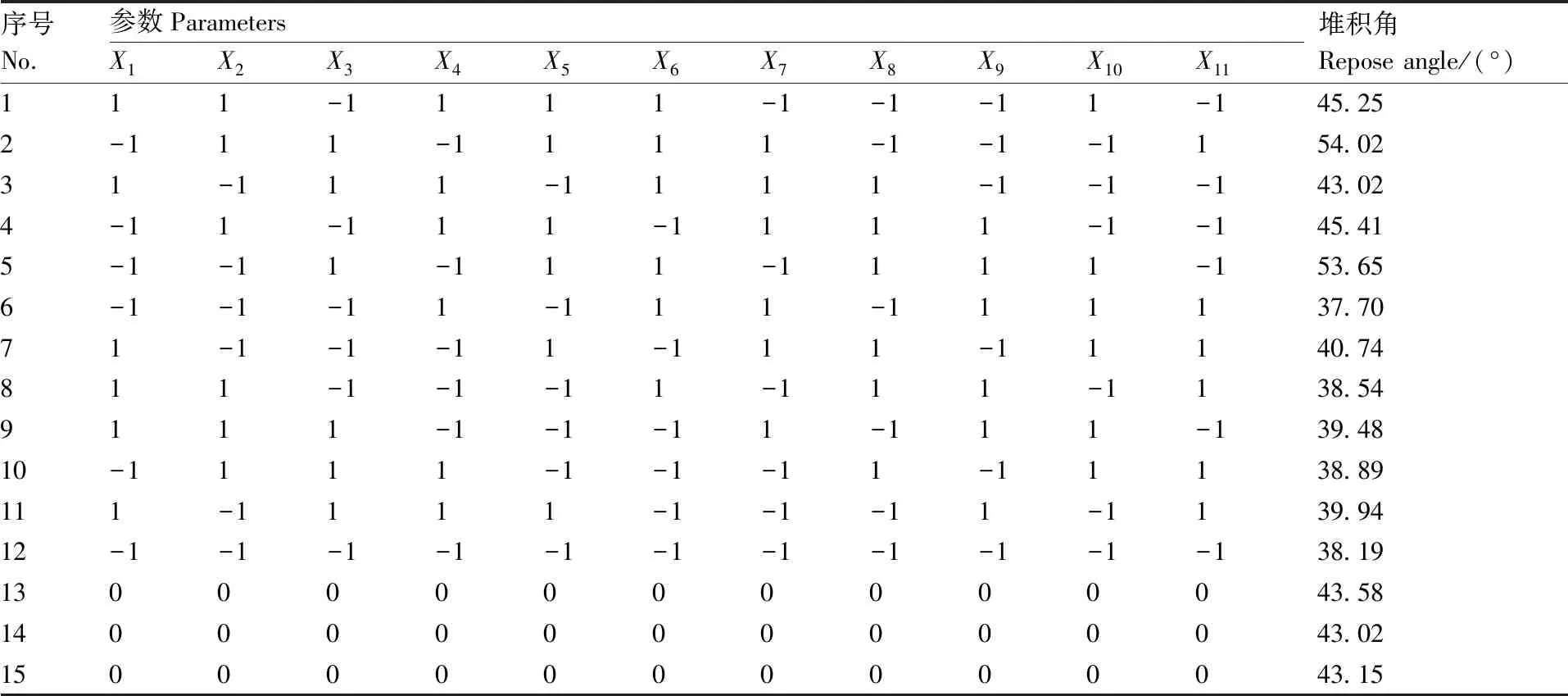
表2 试验设计及结果

表3 试验结果方差分析

3.2 最陡爬坡试验

根据PB试验筛选出的3个显著性参数为、、，为了使这3个显著性参数达到最优区域，基于PB试验结果中显著因素的正效应按确定的固定步长逐渐增加，其余非显著性参数选取中间水平值，进行最陡爬坡试验，并计算黑水虻仿真堆积角与实际堆积角的相对误差，试验方案及结果如表4所示。

由表4可知，随着3个试验参数取值的增加，仿真得到的黑水虻堆积角与物理试验堆积角的相对误差先减小后增大，其中在2号试验对应的参数组合下，得到二者相对误差最小，说明最优的参数水平范围在2号试验附近。因此，以1、2、3号试验中各参数值作为二次回归正交旋转组合试验的-1、0、1水平的因素进行后续的响应面试验。

表4 最陡爬坡试验设计及结果

3.3 响应面试验

根据PB试验筛选出对堆积角的显著影响参数后，以、、为试验参数，结合最陡爬坡试验结果确定各因素试验水平，黑水虻堆积角为试验指标，非显著性试验参数延用表1各因素试验水平并选取表中间水平值。利用Design-Expert软件进行三因素二次回归正交旋转组合试验并进行寻优，仿真试验因素编码如表5所示，试验设计及仿真结果如表6所示。

表5 仿真因素试验编码

表6 试验方案与结果

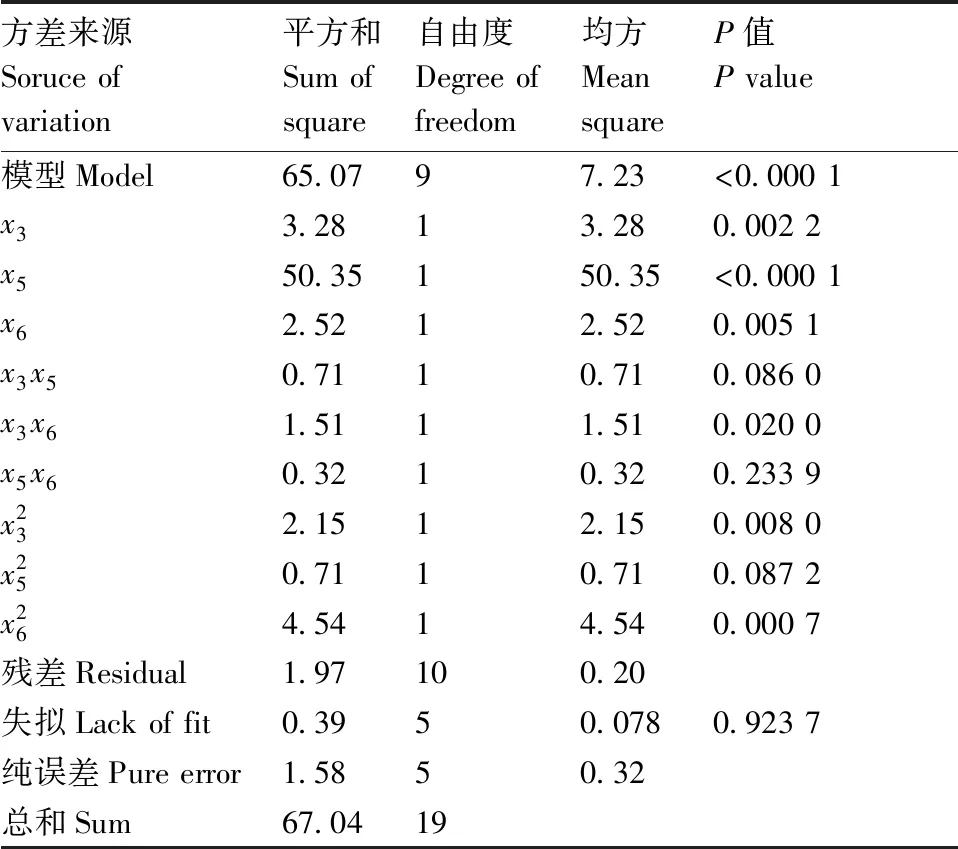
表7 回归方程方差分析

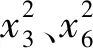
(2)

在保证模型显著、失拟项不显著的情况下，剔除模型不显著的回归项，对模型进行优化，回归方程为

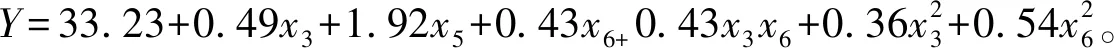
(3)

分析优化后的模型，根据模型的值(<0.000 1)，与模型的失拟项(=0.605 2)可知，模型优化可靠。

由表7所示模型方差分析结果可知，黑水虻剪切模量和黑水虻间滚动摩擦系数的交互项()对黑水虻堆积角影响显著(<0.05)。当黑水虻间静摩擦系数为0.40时，利用Design-Expert 8.0.6仿真软件绘制黑水虻剪切模量和黑水虻间滚动摩擦系数交互作用的响应面图，直观地看到此两个参数之间的交互效应，如图7所示。可以看出，堆积角随黑水虻间滚动摩擦系数变化的曲面变化明显，而随黑水虻剪切模量变化的曲面坡度较为平缓。随着黑水虻剪切模量的增大，堆积角先缓慢减小再缓慢增大。当黑水虻剪切模量为定值时，堆积角随黑水虻间滚动摩擦系数的增加而显著增大。

图7 黑水虻剪切模量与黑水虻间滚动摩擦系数交互作用Fig.7 The interaction between the shear modulus of black soldier fly and the rolling friction coefficient of black soldier fly

4 优化验证试验

为验证黑水虻颗粒组合参数仿真得到的堆积角与实际堆积角之间的相对误差，采用标定后的黑水虻颗粒参数，结合表1设置其他因素水平，进行堆积角仿真试验与实际堆积角试验结果对比，验证优化参数下的仿真试验结果与实际情况的接近程度。基于Design-Expert8.0.6软件的优化模块，以黑水虻实际堆积角为响应目标值对回归方程进行求解并寻优。目标与约束条件方程组为：

(4)

得到多组最佳参数组合，选择其中一组参数得到的仿真结果与物理试验堆积角相对误差最小。同时，考虑黑水虻模型是由多个球形重叠组成，模型外表面与活体黑水虻表面相比，表面存在更多的曲面与凹凸，增加了模型颗粒间的摩擦阻力，流动性降低。因此，选取最优参数时，黑水虻间静摩擦系数与黑水虻间滚动摩擦系数不宜取最大，以提高仿真结果与实际结果的吻合程度。即，黑水虻剪切模量8.67 MPa、黑水虻间静摩擦系数0.43、黑水虻间滚动摩擦系数0.32，其余非显著性因素选择中间水平值(黑水虻泊松比0.3、黑水虻密度350 kg·m、黑水虻间碰撞恢复系数0.2、黑水虻-不锈钢碰撞恢复系数0.3、黑水虻-不锈钢静摩擦系数0.6、黑水虻-不锈钢滚动摩擦系数0.45、JKR表面能0.35 J·m)，其余设置不变，应用EDEM软件进行3次重复试验，得到堆积角均值为35.84°，与箱体抽板法实际测得堆积角34.66°的相对误差为3.40%，无显著差异，如图8所示。试验结果表明3个显著性参数最优值准确可靠。

图8 仿真试验与物理试验对比Fig.8 Comparison of simulation and physical tests

5 结论

(1)结合黑水虻生物特性，以物理堆积试验瞬间获得的黑水虻作为研究对象，采用“Hertz-Mindlin with JKR”作为EDEM离散元仿真模拟的接触模型，应用抽板法进行堆积角试验，标定了黑水虻在接触过程中的物理性能参数。

(2)应用Plackett-Burman试验设计筛选出对黑水虻堆积角有显著影响的参数，包括：黑水虻剪切模量、黑水虻间的静摩擦系数、黑水虻间滚动摩擦系数。结合抽板法堆积物理试验结果，通过最陡爬坡试验确定了3个显著性参数的最优值区域。

(3)基于三因素二次回归正交旋转组合响应面试验，建立了显著性参数与堆积角间的二次回归模型，以堆积角为响应值，对优化后的回归模型进行寻优，确定了EDEM仿真试验中最佳接触参数组合为黑水虻剪切模量为8.67 MPa、黑水虻间静摩擦系数为0.43、黑水虻间滚动摩擦系数为0.32，以最优参数组合得到的仿真试验堆积角为35.84°，与实际测量堆积角相对误差为3.40%，无显著性差异，表明标定黑水虻离散元仿真模型参数准确可靠。