创问题引思维，聚焦核心素养——以“利用导数研究函数的单调性”为例

沈秋彬 福建省长泰第二中学

教育的根本任务在于立德树人。数学教育立德树人的任务体现在让学生会用数学的眼光观察现实世界，会用数学的思维思考现实世界，会用数学的语言表达现实世界，而这需要通过在日常数学教育中经常性渗透核心素养来实现。核心素养的培养从思维开始，思维训练由过程实现，没有过程，就没有思维训练，更谈不上学科素养的培养。

基于参加“指向数学学科核心素养”课堂教学设计比赛，以湘教版《数学》选修2-2第4.3.1节“利用导数研究函数的单调性”（第1课时）为例，分享关于培养学科核心素养的教学设计的实践与思考。

结合章建跃博士提出的三个理解“理解数学、理解学生、理解教学”，因此：

一、结合课程标准，聚焦素养目标

认真解读课程标准是培养核心素养的先决条件。新课程标准对本节课的目标阐述是：结合实例，借助几何直观探索、了解函数单调性与其导数的关系；能利用导数法研究函数的单调性，会求不超过三次的多项式函数的单调区间。在进行教学设计时，若照搬以上目标，可以发现更多关注的是知识与技能目标，没有素养目标，没有具体的行为动词指导教学行为，更别提如何激励学生主动探索知识的形成过程了。

此知识安排在学生已初步掌握了研究导数概念的主要方法后，是极限思想的再延续，此思想也可为后续学习定积分知识进一步提供基本模式和理论基础。虽说如今在高考中将对定积分的考查删除了，但在高中物理知识中，以及今后更高层次的学习中，定积分都是存在的。在分析《普通高中数学课程标准（2017年版）》的要求和本节内容在教材中的地位、作用及编写意图后，挖掘教学内容对培育学生核心素养的价值，把课程目标中涉及的行为动词细化，明确最终要达到的目标，设计学生活动，制订可操作、易于达成的教学目标。综合班级学情，本节课的教学目标是：（1）回顾单调增函数商形式及导数定义的形成过程，结合二次函数对称轴两边过任意一点的切线，观察两切线倾斜角的大小（直观想象）；（2）结合几何画板观察曲线上过动点的切线的斜率的正负变化与曲线单调性的关系，抽象斜率的正负与此点处函数的单调性的关系（直观想象、数学抽象、逻辑推理）；（3）类比二次函数单调性解决办法，自主解答求三次函数单调区间问题，合作由区间得函数图像（数学运算、数学建模、逻辑推理）；（4）构建原函数图像单调性与相应导函数的正负之间的关系（数学建模）。

在领会教材整体性的情况下，制订教学目标，领会编写意图，理解本单元知识的地位和作用，围绕学科素养目标设计教学活动。将目标细分，配上落实素养目标的具体活动，才能真正提升学生的数学核心素养。

二、创问题引思维，发展核心素养

没有问题，就没有思维碰撞。只有让学生思维深度参与，才能发展核心素养。问题设计在最近发展区，让新知识从学生的认知基础出发，生长出来。深刻理解数学知识，应用数学方法，领悟数学思想。

本节课以“利用导数研究函数的单调性方法”的形成过程为核心，依据教学目标及其蕴含的数学核心素养，以及学生的认知特点和心理发展规律，以“从具体到抽象，从特殊到一般”为理念，以问题解决为主线，以独立思考、自主探究、合作交流等学习方式为手段，以培养学生的数学核心素养为目标，从创设情境、构建方法、方法辨析、方法应用这四个方面设计问题，课堂上围绕问题的解决，在解决中促进学生核心素养的形成与发展。

（一）创设情境，切入主题——发展数学抽象素养

问题1：2020最热门的话题无疑是新冠肺炎病毒，其在世界各国先后出现，我们国家在最短的时间内将它有效控制住。图1是3月5日至3月17日我国新增确诊/疑似趋势。同学们观察图形，在这段时间内，新增确诊有什么趋势？

图1

设计意图：通过生活情境引入，构建数学知识，再做研究。让学生感受数学源于生活，又指导生活。

生1：从图1 中可以看出，随时间的变化整体上有明显下降的趋势，但在3 月12 日至3 月17 日有小幅上升趋势。

问题2：若把此图视为以时间为自变量的函数图像，图像的上升与下降可用哪个知识点描述？

生1：单调性。

（二）思维类比，构建方法——发展数学抽象素养

必修1 中单调增函数的定义常常改写成：对于任意x1、x2∈I，当x1≠x2时，有成立。

问题3：结合两点间斜率公式，如何从几何角度解释单调增函数的定义？

生2：画图，合作得出割线的斜率大于0，函数单调递增。

设计意图：数无形缺直观，当遇到难以解决的函数问题时，数形结合方法是好方法。

问题4：结合几何画板发现割线的斜率与函数的单调性紧密相连。因此要研究导数与函数的单调性的关系，可以先研究一下割线的斜率与导数的关系。

图2

生3：取极限，割线的斜率变切线的斜率。

师：可发现曲线上任意点附近的曲线可被该点处的切线近似替代，“以直代曲”是导数的本质思想，因此可将曲线的上升或下降问题转化为切线的斜率问题。

利用几何画板，移动点P，观察过点P的切线的斜率与点P附近曲线的变化规律。

图3

问题5：填空：f ′（x0）______________时，曲线经过点P时，有上升趋势；f ′（x0）______________时，曲线经过点P时，有下降趋势。

生4：＞，＜。

活动说明：据图学生不难写出正确答案，教师补充说明f′（x0）=0是在x0处的切线的斜率等于0，即f（x）在x0处的切线与x轴平行，因此可以认为此时没有上升或下降。

问题6：若点P处的导数符号刻画的是曲线f（x）在点P处的上升（下降）趋势，那么如何刻画在一个区间上的函数单调性呢？

对于任意x∈（a，b），有________，则函数f（x）在（a，b）上单调递增。

对于任意x∈（a，b），有________，则函数f（x）在（a，b）上单调递减。

设计意图：通过从特殊到一般、直观到抽象的研究过程，渗透数学研究的一般方法，引导学生构建结论，发展学生的逻辑思维及数学抽象思维，总结导数的正负与函数的单调性的关系。

（三）自主探究，方法辨析——发展学生的数学逻辑推理素养

问题7：为什么要引进导数来研究函数的单调性呢？接下来找找答案。

例1用以前学习的方法求函数f（x）=x2-4x+3的单调区间，比比谁更快求出来。

学生做题，并对比同桌及旁边的同学的方法。

设计意图：对于熟悉的二次函数，学生首先想到的是画图，作图成关键，是不是高中所有的函数都可以很快画图？

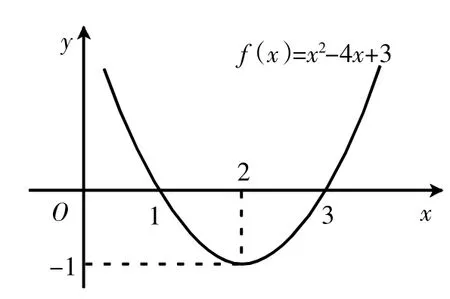
图4

法一：图像观察法。

法二：定义法。

法三：导数法，并小结解题步骤。

（四）合作交流，方法应用——发展数学运算、建模素养

求二次函数的单调性的三种方法是否适用于三次函数？现我们来看看：

变式：（1）f（x）=x3-2x2+x-1，确定f（x）的单调区间。

（2）在（1）的基础上，画出f（x）的大致图像。

（3）原函数的单调性与导函数的图像之间是否有关系？若有，是什么关系？

学生活动：前后桌一起讨论，请同桌讲讲解题的策略。

设计意图：此题回答了为何要引进导数法研究函数的单调性。第（2）问更是需要学生会将数转化为形，引导学生数形结合。第（3）问引导学生构建解题的一般模式，发展学生的逻辑思维、直观想象，为今后学习三次函数的极值奠定理论基础。

图5

例2请用导数法证明f（x）=sinx-x在区间（0，π）上是减函数。

变式：请思考该函数在区间（-π，π）上的导函数的符号。

设计意图：对利用导数法求单调性的充分与必要性进行辨析。

图6

三、结束语

综上所述，课前要深入钻研课程标准和教材，理解数学，把握数学知识的整体性，理解数学本质；考虑学情，理解学生，创设情境、反复推敲问题，提出梯次问题，安排学生活动；理解教学，设计好每一节课，将本节课的核心素养目标划分并落实到课堂教学中。有一句话这么说：“本科生玩解题技巧，学霸玩解题思想。”我觉得挺形象的。教学中渗透数学思想的重要性不言而喻，如何让学生感受数学思想，领悟数学思想方法，运用数学思想方法分析、思考问题，升华成学生的思维，从而达到立人，这才是教育之根本。