高考数学圆锥曲线解题技巧研究

姬彩生

(江苏省徐州市第七中学 221011)

众所周知，高考中时间紧迫，要想取得理想成绩，提高圆锥曲线解题效率尤为关键.为避免学生在解题中少走弯路，教学中既要启发学生认真审题，又要做好相关解题技巧的灌输，使学生真正消化吸收，在解题中灵活应用.

1 借助相关结论解题

解答圆锥曲线习题时利用相关的结论既能保证解题的正确性，又能节省解题时间，因此，教学中应注重为学生讲解有关圆锥曲线的相关结论，要求学生根据所学进行推导.同时，为学生展示结论在解题中的应用，给其留下深刻的印象，提高其利用相关结论的解题意识.

该结论可要求学生自己进行证明.

解析根据题意，设直线AP的斜率为k1，因为A(-a，0)，则其方程为y=k1(x+a).

令x=a，则y=2k1a.

则点M的坐标为(a，2k1a).

2 借助几何知识解题

解答部分圆锥曲线习题时运用几何知识可简化解题过程，因此，教学中与学生一起总结与圆锥曲线相关的几何知识，如线段的平行、垂直，三角形的相似等，并为学生展示几何知识的应用，使其体会借助几何知识解题的便利，为其更好地运用于解题中做好铺垫.

图1

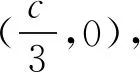
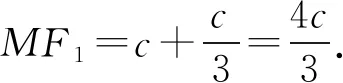
连接PF1,QM，则PF1∥QM.

所以PF1=b.

由椭圆定义可知PF=2a-b.

又因为点Q为直线PF和圆的切点，

则QM⊥PF.

所以∠F1PF=90°.

即(2a-b)2+b2=4c2.

又因为c2=a2-b2，不难得出

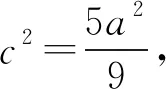
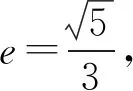
3 借助坐标运算解题

坐标运算是解答圆锥曲线习题的重要思路之一.教学中为使学生掌握运用坐标运算解题的技巧，应做好相关例题的优选与精讲，以更好地拓展学生的解题思维，使其具体情况具体分析，选择最优的解题方法.

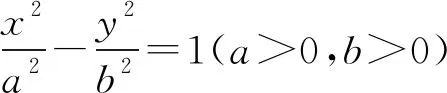
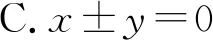
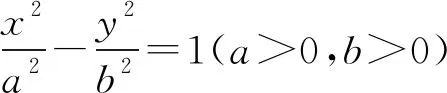
设A(x0，y0)，B(x1，y1)，则D(-x1，-y1).

又因为平行四边形ABCD的四个顶点均在该双曲线上，所以

①

②

①-②，得

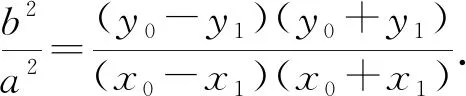
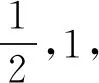
故选A.

4 借助参数方程解题

使用参数方程解答圆锥曲线习题可很好地提高解题效率.教学中应为学生讲解直线以及圆锥曲线参数方程，使其明确不同参数表示的含义，更好地把握参数方程本质，尤其为学生示范参数方程在解题中的应用，使其把握相关的应用细节.

解析根据题意可设直线的参数方程为

将其和抛物线方程联立整理，得

设A,B对应的参数为t1,t2，

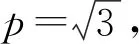
高考中圆锥曲线习题类型灵活多变，解题思路也不尽相同.为提高学生解答不同题型的能力，在传授解题技巧的同时，认真讲解解题技巧的具体应用，使学生深入理解，把握相关解题技巧的细节，使其遇到相关题型，能够快速、高效、正确求解.