解析21年新高考Ⅰ卷第19题的六个视角

刘才华

(山东省泰安市宁阳第一中学 271400)

解三角形是高中数学教学的重要内容，也是高考考查的主要内容之一.《普通高中数学课程标准》对其有如下要求：(1)借助向量的运算，探索三角形边长与角度的关系，掌握余弦定理、正弦定理；(2)能用余弦定理、正弦定理解决简单的实际问题.从近年来全国高考数学试题来看，解三角形一般是一道主观解答题，总分12分，约占全卷总分的8%，难度整体上相对保持稳定，难易适中.试题一般结构简单，内涵丰富，除考查余弦定理和正弦定理外，还常常和三角变换公式、平面几何、平面向量、函数和不等式等知识相结合，对学生的数学运算、逻辑推理、综合解题能力有较高要求.

1 试题呈现

题目(2021年全国新高考Ⅰ卷第19题)如图1，记△ABC的内角A,B,C的对边分别为a,b,c.已知b2=ac，点D在边AC上，BDsin∠ABC=asinC.

图1

(1)证明：BD=b；

(2)若AD=2DC，求cos∠ABC.

这是2021年全国新高考数学Ⅰ卷第19题，属于解三角形中的给值求值题型，试题以三角形为载体，简洁明快，综合考查了学生利用解三角形和三角变换等相关知识分析问题和解决问题的能力.

2 试题解析

2.1 第(1)问解析

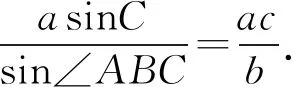
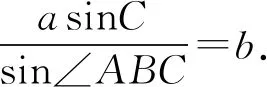
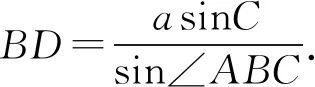
所以BD=b.

2.2 第(2)问解析

对于第(2)问，如何利用好条件“b2=ac”和“AD=2DC”是解题的关键所在.

为行文方便，由题意我们约定CD=t，则AD=2t,AC=BD=3t，∠ADB=θ.

解法1不妨设CD=t=1，则由(1)和题意得b=BD=3，AD=2.

由余弦定理,得a2=9+1-6cos∠BDC，

c2=9+4-12cos∠BDA.

因为∠BDC+∠BDA=π，

所以2a2+c2=33.

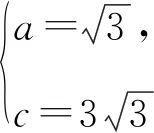
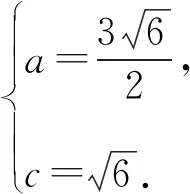
解法2 由(1)知BD=b.

在△ABD中，由余弦定理,得

在△ABC中，由余弦定理，得

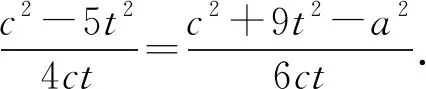
即2a2+c2-33t2=0.

c4-33t2c2+162t4=0.

即(c2-6t2)(c2-27t2)=0.

则c2=6t2或c2=27t2.

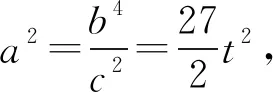
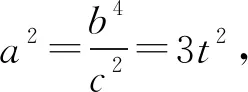
解法3由(1)知BD=b.

在△ABD中，由余弦定理，得

AB2=AD2+BD2-2AD·BDcosθ.

即c2=13t2-12t2cosθ.

在△CDB中，由余弦定理,得

a2=10t2-6t2cos(π-θ)=10t2+6t2cosθ.

由b2=ac,得b4=a2c2.

则81t4=(10t2+6t2cosθ)(13t2-12t2cosθ).

则72cos2θ+42cosθ-49=0.

代入c2=13t2-12t2cosθ,得c2=6t2.

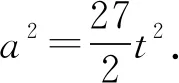
解法4由(1)知BD=b.

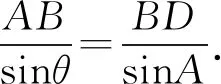
即csinA=bsinθ.

又asinB=bsinA，两式相乘,得

acsinAsinB=b2sinAsinθ.

由b2=ac和sinA≠0，则sinB=sinθ.

在△ABC中，由余弦定理,得

b2=a2+c2-2accosB=a2+c2-2b2cosB.

则b2(1+2cosB)=a2+c2.

即9t2(1+2cosB)=a2+c2.

①

同理，

AB2=AD2+BD2-2AD·BDcosθ.

即c2=13t2-12t2cosθ.

在△CDB中，a2=10t2+6t2cosθ.

从而a2+c2=23t2-6t2cosθ.

②

若∠ABC=∠BDC，则cos∠ABC=-cosθ.

解法5由(1)知BD=b.则

从而sinABC=sinθ.

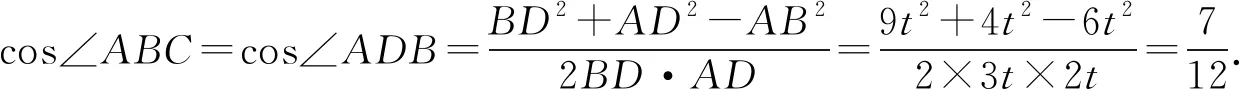
在△CDB中，BD>BC+CD，不成立.

解法6 由(1)知BD=b.

由AD=2DC,

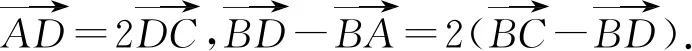
整理,得11b2=6a2+3c2.

由b2=ac,得11ac=6a2+3c2.

即(2a-3c)(3a-c)=0.

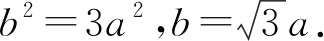
此时c>a+b，不成立.

解法7由(1)知BD=b.

以点B为坐标原点，以直线BC为x轴建立直角坐标系，则C(a,0)，A(ccos∠ABC,csin∠ABC).

设D(x,y)，则

(x-ccos∠ABC,y-csin∠ABC)=2(a-x,-y).

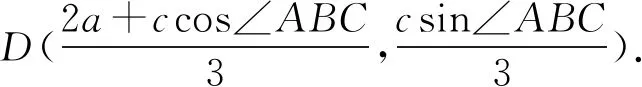
由|BD|=b,得

(2a+ccos∠ABC)2+(csin∠ABC)2=9b2.

③

11b2=6a2+3c2.

由b2=ac,得11ac=6a2+3c2.

即(2a-3c)(3a-c)=0.

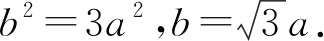
此时c>a+b，不成立.

解法8由(1)知BD=b.

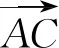
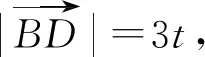
由b2=ac,

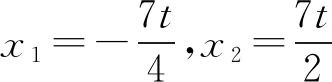
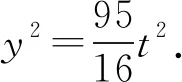
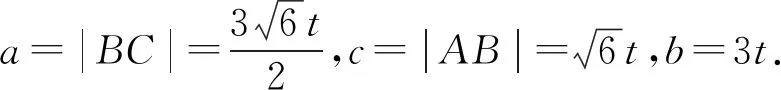
解法9(利用斯特瓦特定理)

由(1)知BD=b.由斯特瓦特定理,得

即2a2+c2=33t2.

结合b2=ac=9t2，得6a2-11a+3c2=0，

下同解法6.

托勒密定理圆的内接凸四边形两对对边乘积的和等于两条对角线的乘积.

解法10(利用托勒密定理) 由(1)知BD=b.设直线BD交△ABC的外接圆于点E，由相交弦定理，得AD·CD=BD·ED.

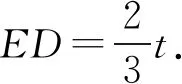
由托勒密定理,得

AB·CE+BC·AE=AC·BE.

将相关数据代入,得6a2-11a+3c2=0.

下同解法6.

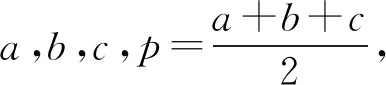
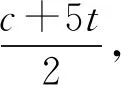
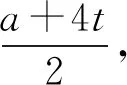
由AD=2DC,得S△ABD=2S△BCD.

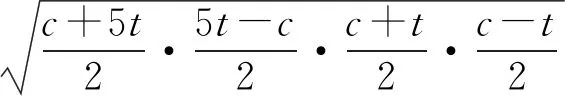
将b2=ac=9t2代入，得6a2-11a+3c2=0.

下同解法6.

教学启示通过对上述试题不同解法探讨，启发我们在平时数学教学时，要结合具体内容，做好一题多解的训练，提高学生学习数学的兴趣，有效地避免题海战术.通过加强一题多解训练，培养学生的发散性思维，引导学生利用不同的视角、不同的方法和不同的运算去分析同一道试题，发挥学生解题的灵活性和创新性，这对于培养学生的数学运算、逻辑推理等素养大有裨益.