分而用之 触类旁通——分类讨论思想在初中数学教学中的渗透

周书娜

(江苏省南京市竹山中学湖东路校区 211100)

数学课程标准把数学思想教学作为课程目标之一.笔者在多年的教学实践表明:有很多学生由于没有掌握正确的数学思想，导致学习数学老是不能进步，上升空间有限，这也说明他们没有深入认识到数学思想是数学思维的核心.一味地做题、刷题达不到预期的效果.有时我们作为教师在教学时也会只关注知识的结果，忽视知识的形成过程中所存在的数学思想，导致学生的数学思想得不到培养，考试遇到灵活性和比较难的问题就不知道怎么做.特别是解决与分类讨论有关的问题时，出现不知道分类、不会分类、分类不全面等问题.而分类讨论思想在初中阶段运用范围比较广泛，可见在初中数学教学中要重视分类讨论思想.

什么是分类讨论思想? 一般情况下，如果题目所给的条件无法确定，无法用统一的方法进行解答，需要将这个问题分成几种情况，每种情况逐一研究解决，最后将各种情况下的解进行归纳整合.针对分类讨论思想在数学教学的思考，我将从以下几个方面进行阐述：

1 初中数学分类讨论思想运用步骤与基础

1.1 分类讨论运用步骤

数学教学中运用分类讨论，首先需结合题目要求，对问题进行细化分析，有效确定讨论目标，然后再根据研究目标实施讨论，最后归纳总结得到结论.初中数学教学中运用分类讨论思想，可结合对应步骤实施教学.在运用中每次的分类都要依据一定衡量标准进行分类，让学生在使用分类思想的时候不遗漏，不重复.因此为了保证分类讨论思想的全面性与系统性，需依照一定研究目标实施教学，进行综合性讨论.

1.2 运用分类讨论思想的基础

初中数学分类教学在具体实施的时候，对于一些问题不能进行统一研究时，就要以一定标准实施分类讨论.此过程中学生要明确讨论对象与范围，确定分类的标准.分类讨论思想不是所有问题都适用的，因此学生要知道哪些题目解决的时候需要运用分类讨论.例如，等腰三角形已知一个角求另外两个角，或者已知一条边求另外两条边，看到这种类型的题目就要立刻想到分类讨论.

2 不同教学环节渗透分类讨论思想策略

2.1 在新授课中渗透分类讨论思想

在初中数学教材中，有很多知识的探索需要用到分类讨论思想.教师上课的时候紧扣教材就能很好地渗透分类讨论思想.

例如：七年级上册第2章有理数，这章有很多分类讨论的内容.首先是有理数的概念这节课，要求会按照不同的标准对有理数进行分类.其次从正数、负数、零三个角度研究绝对值.然后是从同号、异号、零这三个方面研究有理数加法法则、乘法法则.最后是从正数和负数两方面研究有理数的乘方.第3章代数式中比较两个代数式大小时，也会用到分类讨论的思想.第5章走进图形世界，需要学生按照一定的标准将图形进行分类.第6章平面图形的认识(一)，学习平行线这节课时，在引入两条直线位置关系的时候也会用到分类的思想.又如八年级第一学期的几何教学，第2章这一章节，课堂上在研究线段垂直平分线性质定理和判定定理时，需要将点与线段的位置进行分类.证明有一个角是60度的等腰三角形是等边三角形时，需要将60度的角进行分类.特别是等腰三角形的练习题中也有很多需要分类讨论的，该章节分类讨论出现的较为多，学习这一章节时，教师要好好利用教材重点强化学生分类讨论意识.

其实，每个年级的教学内容都会涉及到分类讨论，教师需要充分地研究教材、把握教材，在探讨知识的过程中无形地渗透分类讨论的思想，让学生有分类讨论的意识.

2.2 通过解题渗透分类讨论思想

在讲授新课知识过程中向学生渗透分类讨论的思想是一个比较漫长的过程，对于初中刚入学的学生是个比较好的方法.对于高年级的学生，为了让学生能更好地掌握分类讨论，可以设置相关专题，让学生学会从哪些方面去分类，怎样分类不遗漏、不重复，强化学生的分类讨论意识.选取的题目要有价值，不是盲目性地选题.可以从以下几个方面来选题：窗体顶端在讲授新课知识过程中向学生渗透分类讨论的思想是一个比较漫长的过程，对于初中刚入学的学生是个比较好的方法.而对于初三学生，为了让学生能更好地掌握分类讨论，可以设置相关专题，让学生学会从哪些方面去分类，怎样分类不遗漏、不重复，通过巩固练习来强化学生的分类讨论意识.

例1关于x的方程(k-2)x2-2kx+k=6有实数根，求k的取值范围.

分析：本道题是由概念引起的分类讨论.从方程的概念进行分类，这个方程可以是一元一次方程，也可以是一元二次方程.

解(1)若k-2=0，即k=2时,-4x+2=6是一元一次方程，有实数根.

(2)若k-2≠0，即k≠2时 (k-2)x2-2kx+k-6=0是一元二次方程a=k-2，b=-2k，c=k-6

因为一元二次方程有实数根,所以b2-4ac≥0,4k2-4(k-2)(k-6)≥0

k≥6

综上所述，k≥6或k=2.

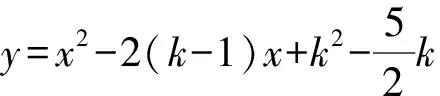
(1)若抛物线与x轴有两个不同的交点，求k的取值范围；

(2)若抛物线经过点(2k,y1)和点(2,y2)，且y1>y2，求k的取值范围；

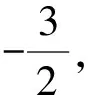
分析本题(1)、(2)两小问不需要用到分类讨论，比较基础，只要计算时细心一点就没什么问题.而第(3)小问，由于函数表达式里系数含有字母，导致对称轴的位置不能确定，于是在给定范围内，看不出函数的增减性，无法求出最小值，因此需要对对称轴的位置进行分类讨论.可是学生由于缺少分类讨论的意识，大部分学生第(3)小问留白，少部分没有分类讨论，直接求了在顶点处有最小值，得分率比较低.

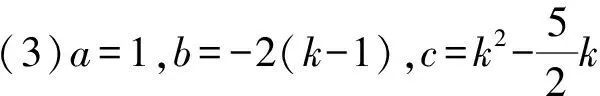
①若k<1，当1≤x≤2时，y随x的增大而增大

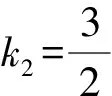
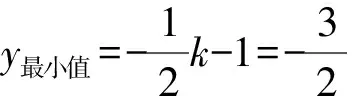
解得k=1

③若k>2，当1≤x≤2时，y随x的增大而减小

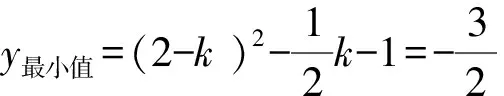
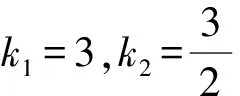
综上所述，k=1或k=3.

以上二道例题就是需要用到分类讨论思想的题型：由概念、公式、法则引起的分类，由含有字母系数引起的分类，由不确定的图形或位置引起的分类.在解题过程中，我发现学生会出现无从入手或者答案不全面，错误率比较高，其实这和学生缺失分类讨论思想有关.

3 分类讨论思想渗透的注意事项

3.1 低起点渗透分类思想

很多数学知识的产生都伴随数学思想，但是经过对初中生分类讨论思想的理解与运用情况进行调查，发现其问题多集中在“难”上，很多学生无从下手，不知道怎么分类.另外教师的教学也存在一些困惑，数学分类思想比较抽象，学生较难理解.实际上数学教学中基础知识的教学也渗透了数学思想，但因为学生轻松理解，所以忽视了其中渗透的分类讨论思想.在此要降低起点，发挥基础知识载体性，科学渗透数学思想，帮助学生理解.

3.2 注重信息技术的运用

信息技术为数学教学增添趣味性，分类讨论思想的运用虽然出现，但是必要的时候运用信息技术手段，可让教师在数学思想的渗透教学中起到事半功倍的效果.几何画板作为专业性强的数学教学软件，在其动态展示的时候可呈现数学的本质，进而渗透分类讨论思想.如研究圆周角与圆心位置关系的时候，学生凭空想象比较困难，借助几何画板的动态演示，让学生既能快速地发现圆周角与圆心的3种位置关系，也能让学生体会到分类讨论的思想.

总之，分类讨论的思想对于学生学好数学是有价值的.“路漫漫其修远兮，吾将上下而求索”，想短暂时间就能形成和培养分类讨论思想，这显然不现实，需要教师在课堂教学中经过长期地、反复地渗透和训练.