基于粒子轨迹的危岩体损伤识别研究

赵 晨 谢谟文 刘卫南 路 光

(1.北京科技大学土木与资源工程学院,北京 100083;2.城市地下空间工程北京市重点实验室,北京 100083)

岩崩作为常见的影响人民生命与财产安全的边坡地质灾害,具有分布广、危害大、突发性强等特点,对矿山、路桥等工程产生重大隐患。由于危岩失稳破坏突发难以察觉,危岩体的早期识别与监测预警已成为工程勘测中的难点问题。目前常用的危岩体稳定性评价手段有遥感监测、稳定性评价模型、关键指标趋势监测等,遥感监测多为利用无人机影像[1]、激光点云[2]、InSAR[3]等遥感手段基于危岩结构面产状的解译体系,此方法依赖于工程经验进行定性评估;稳定性评价模型[4],此方法所需的主控结构面尺寸等参数难以准确测量;关键指标趋势监测[5],如:裂缝深度、位移、应力等。然而危岩体失稳属脆性破坏,上述指标变幅微小且时效性差,难以实现危岩损伤识别与崩塌早期预警。

目前,基于振动力学的损伤检测手段已被广泛应用于结构工程与机械工程等领域。近年来对危岩体损伤机理的深入研究发现[6-8],岩崩作为一种动力破坏过程,动力学特征(如阻尼比、振幅比、固有频率等)与危岩体稳定性具有相关性。危岩体内部损伤导致振动形式改变,相关动力学指标变化。叶阳升等[6]通过实验分析坠落式危岩体振动特性,结果表明危岩体损伤前后卓越频率、振幅比变化显著。贾艳昌等[9]建立了基于固有频率的危岩体稳定性评价模型,避免了危岩体稳定性定量评价时对主控结构面参数的直接测量。然而,非平稳信号频域分析受采集频率、时频转换算法影响较大。近年来,杜岩等[7]提出了基于变异系数、峭度等多时域动力学指标的危岩体损伤识别方法。上述方法均基于单向时间序列做时频指标分析。然而,振动指标变化与岩桥损伤部位和风化方向密切相关。仅凭单一方向振动响应显然无法全面反映危岩体稳定性,损伤识别准确性与敏感性存在限制。危岩体运动是多方向多振型耦合而成[10],相较之下,空间运动轨迹包含信息量更多。

近似熵作为评价系统复杂程度的物理量,可定量评价时间序列不规则性,在机械工程[11]、结构工程[12]、生物医学[13]等领域的诊断检测应用已较为成熟。胥永刚等[14]利用二维近似熵评价机械损伤后轴心运动轨迹复杂性,实现了大型机械故障诊断。谢中凯等[15]将互相关近似熵应用于土木工程领域,通过分析混凝土梁损伤前后自由振动差异程度,实现了混凝土结构损伤识别。上述研究为危岩体损伤识别提供了启发。本研究以危岩体岩桥损伤对运动轨迹产生影响为基础,将互相关近似熵予以改进,扩展至三维时间序列,用于评价危岩体损伤前后自由振动粒子轨迹差异性。结合模型试验,分析危岩体损伤加深时,空间运动轨迹与初始稳定状态差异程度,探究粒子轨迹熵在危岩体损伤识别领域的适用性。

1 研究方法

1.1 基于粒子轨迹的危岩体岩桥损伤识别

边坡母岩以岩桥约束危岩体运动,危岩体振动形式可反映岩桥损伤。将母岩对危岩体的约束视为弹簧—阻尼系统,自然界中岩桥损伤弱化可对应于弹簧对危岩体约束减弱。杜岩[16]提出将危岩体自由振动视为单自由度弹簧质子型振动。危岩体动力学简化模型如图1所示。

图1 危岩体弹簧质子型振动简化模型Fig.1 Simplified model of spring plasmonic vibration of hazardous rock masses

危岩体单自由度欠阻尼自由振动时动力学方程如下:

式中,ω0为危岩体固有频率;ζ为阻尼比。

代入初始条件,解得式(1)反映物体振动状态的动力学指标:

式中,m为岩体质量;c为阻尼系数;k为弹簧刚度,与岩桥约束强度相关。

式中,E为岩体弹性模量;H与S分别为岩桥厚度与面积。

联立解得:

由式(5)、式(6)可得,危岩体的固有频率、阻尼比均与岩桥约束强度相关。危岩体损伤实质是岩桥强度弱化与锁固面积减小。自然风化下,危岩体与母岩相连的岩桥面积S或弹性模量E减小,危岩体所受约束减弱,阻尼比与频率均改变,宏观体现于运动形式变化。

现实中危岩体是多自由度的,其运动形式是多阶振型耦合的结果,包括横、竖向摆型振动、扭转振动、纵向振动等。由于母岩通过空间中X、Y、Z3个方向刚度约束危岩体,自然环境中结构面产状不同且损伤方向各异,岩桥不同方向损伤对各振型影响并不同。例如,当后缘裂缝沿纵向加深时,危岩体水平向刚度却无明显弱化,则不同方向动力学指标敏感性各异。相比分析单一方向振动,岩桥任意方向损伤均可反映于岩块的运动轨迹中,因此空间运动轨迹可更充分反映危岩体稳定性。

1.2 基于互相关近似熵的粒子轨迹差异性评价

目前常以最大幅值角度评价危岩体运动轨迹,由于环境噪声和激励特征难以控制,幅值具有不确定性,难以体现危岩体自身性质。近似熵概念由Pincus提出,描述时间序列中生成新模式的概率大小,用于度量时间序列复杂度。近似熵具有抗噪性强、数据量要求低且与幅值无关的优点[13],其值与时间序列复杂度呈负相关,常见正弦信号约为0,白噪声约为1.5[17]。互相关近似熵[18]是在近似熵基础上的改进,对两期时间序列的互相关函数计算近似熵,反映时间序列差异程度。谢中凯等[15]通过模拟信号与室内试验证实当结构裂缝加深、固有频率降低时,混凝土梁损伤前后振动信号相似性下降,互相关函数频率组分增多,近似熵增加。由1.1节所述,危岩体后缘岩桥损伤时,运动形式将发生变化。日本土木研究所藤泽团队监测边坡危岩块体粒子轨迹发现,不稳定岩块与稳定岩块相比振动差异明显且方向改变。由于危岩块体损伤前后自由振动轨迹相似性被削弱,其互相关函数不规则性增强,近似熵增加。

本研究提出粒子轨迹熵指标(Particle Trajectory Entropy,PTE),将常规用于一维时间序列的互相关近似熵扩展至三维,用于评价损伤前后危岩空间运动轨迹差异性。具体算法如下:

已知危岩体粒子轨迹的三维时间序列U(i)={X(i),Y(i),Z(i)},i=1,2,…,N。对2组序列中3个分量分别做互相关计算得到R(i)={rx(i),ry(i),rz(i)}。

(1)对时间序列加窗,得到k=n-l+1个l维向量的子序列:

(2)计算子序列与其余子序列的距离s,得到k个集合Si:

定义阈值f,统计每个集合Si中达到阈值限的个数占总数n-l+1的比值,以表示。对取对数平均值:

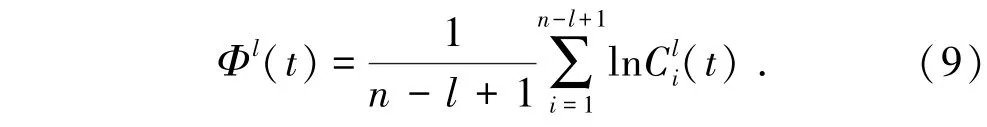
将窗长l更新为l+1,重复步骤(1)、步骤(2)。定义互相关近似熵:

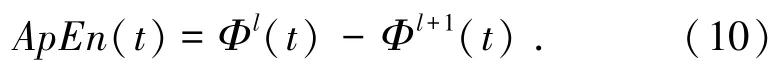
由上述算法可知,近似熵是对时间序列进行自相关分析,即窗长变化时产生新模式的概率,与频率组份增减和频率自身变化密切相关。算法需定义参数l、f与n。近似熵对样本量n要求较低,1 000个数据即可。前人通过实践权衡计算效率与结果精确度[11],建议窗的长度l通常取2,阈值f取序列标准差STD的0.1～0.2倍。本研究取β=0.2,l=2,则对于三维互相关近似熵:

2 模型试验

2.1 试验设计

为证明上述研究的实用性,设计相似模拟试验验证。以坠落式危岩体为例,危岩块体尺寸20 cm×20 cm×20 cm,采用重晶石粉、石英砂为骨料,石膏为粘结剂,外加甘油、缓凝剂与水浇筑而成。利用石膏作为岩桥将岩块粘结于室外墙体,岩块其余各面临空,模拟坠落型危岩体失稳破坏。岩块顶部布设一枚三向拾振器。为模拟现场实际条件,本实验于室外进行。模型简图与现场照片如图2所示。

图2 试验模型简图及现场照片Fig.2 Photo and sketch of test model

试验通过逐步切割石膏延长后缘裂缝深度模拟岩桥不同程度损伤,共分为7个损伤阶段,步长增量统一为2 cm。利用激振锤对各损伤阶段时岩块顶部施加沿Z轴负方向激振,记录其三向动力响应。采样时间1 s,采样频率1 500 Hz。

2.2 数据采集与提取

本试验采用COINV振动监测系统采集岩块振动数据,包括采集仪、激振捶与三向拾振器,如图 3所示。

图3 实验设备Fig.3 Experimental equipment

每个损伤阶段采集3组数据,以平均值作为实测值。提取多个常用时、频域动力学指标,分析其与岩桥损伤的相关性。具体算法如表1所示,表1时间序列分析中相关参数如下:Aσ表示标准差;表示平均值;Arms表示均方根;p表示绝对值平均值;N表示数据量;ai表示时间序列i时刻的幅值,FFT表示快速傅里叶变换。

2.3 试验结果分析

首先计算常用时、频域动力学指标,得到X、Y、Z3个方向指标变化趋势如图4所示。

图4 时、频域指标变化情况Fig.4 Changes in time and frequency domain indicators

分析表1中指标,其中峭度、偏度、冲击因子、波形因子与变异系数在3个方向变化趋势并不相同且波动无规律。原因可能是由于环境噪声和激振特征对时域指标产生影响,局限性较大。仅有固有频率变化趋势随岩桥损伤表现出相关性。对固有频率做进一步分析,不同振动方向固有频率衰减率差别较大。上述现象是由于岩桥不同损伤形式对不同方向自由度约束的削弱有区别,对危岩体振动影响存在差异。因此将固有频率用于识别危岩体损伤时,为保证结果准确,需明确结构面损伤方向与损伤形式。合成岩块时程数据,得到其粒子轨迹,部分粒子轨迹如图5所示。

表1 时、频域指标算法Table 1 Time and frequency domain indicators algorithm

图5 不同裂缝深度下岩块粒子轨迹Fig.5 Trajectory of rock mass particle under different fracture depth

由图5可知,与未损伤时相比,随岩桥锁固面积 减小,粒子轨迹相似性下降。危岩振幅衰减变缓且周期增加,揭示阻尼比与频率随岩桥损伤发生变化。此外,岩桥损伤对危岩不同方向振动影响不同,X向振动较Y向振动变化更为明显。以岩桥未损伤时的粒子轨迹为基础态,分别将各损伤程度下的危岩粒子轨迹与基础态对比,计算互相关近似熵,如表2所示。分析粒子轨迹熵变化趋势与岩桥损伤的相关性,粒子轨迹熵由0.103增至0.602。表明随岩桥损伤程度加深,危岩体粒子轨迹与基础态的相似性逐渐降低,粒子轨迹熵变化趋势相较于上述时、频域指标,与危岩体损伤相关性优势明显。

表2 各损伤阶段粒子轨迹熵变化情况Table 2 Entropy of particle trajectories in each damage phase

为探究不同材料时粒子轨迹熵普适性,调整材料中重晶石粉配比降低岩块密度,重复上述试验。低密度岩块粒子轨迹熵由0.062增至0.310,2次试验指标变化趋势类似,可见利用粒子轨迹差异性识别危岩损伤对不同密度材料适用性较好。

进一步分析粒子轨迹熵与固有频率变化对岩桥损伤的敏感性。为便于指标对比,敏感性定义为指标随岩桥损伤相对变化程度。岩桥损伤程度β以损伤后实际长度ln与原始长度l0之比表示。

指标变化程度γ以损伤前后指标变化量Δα与初或末时刻的指标α0之比表示,对于递增曲线,α0取初时刻,对于递减曲线取末时刻。

损伤前粒子轨迹熵定义为对未损伤粒子轨迹自相关计算所得近似熵。结果如图6所示。

图6 指标变化程度比较Fig.6 Comparison of the degree of change in indicators

对比指标变化程度,粒子轨迹熵相比初时刻上涨5倍,且损伤前期变化明显。由图4(f)可知,X方向固有频率与Z方向变化相似,因此仅分析Z方向与Y方向固有频率变化程度。Z方向与Y方向固有频率相比末时刻分别变化约0.8倍与0.14倍。相较之下粒子轨迹熵对识别危岩体损伤敏感性与时效性更高。

3 结 论

通过分析危岩体动力学机理,结合信息熵理论,引入粒子轨迹熵概念。将粒子轨迹作为危岩体损伤识别指标,利用三维互相关近似熵评价其损伤前后自由振动粒子轨迹差异性,并进行试验验证。得到以下结论与思考:

(1)主控结构面的力学性质与锁固面积是危岩体保持稳定的关键。随岩桥约束能力弱化,危岩体自由振动的频率、阻尼比、方向均发生变化。危岩体空间运动轨迹可反映危岩体运动形式的改变。

(2)将互相关近似熵扩展至三维,评价损伤前后危岩体粒子轨迹差异性。试验结果表明随岩桥锁固面积减小,粒子轨迹熵逐渐增大,与传统时、频域监测指标相比,敏感性显著。此外,粒子轨迹熵对不同密度材料具有普适性。将其用于危岩体岩损伤识别,具有一定应用前景。

(3)粒子轨迹熵对危岩体损伤识别依赖于两期数据对比,而且只能实现对损伤程度定性评价,确定基于粒子轨迹熵的崩塌早期预警普适性阈值是下一阶段研究方向。