关注代数式结构 发展数学抽象素养——以高三一模考试中的“同构函数”为例

安徽省寿县第一中学 柴化安 （邮编：232200）

1 问题呈现

2022年高三复习渐入佳境，各地市一模陆续进行，命题人与时俱进，试题以数学核心素养为导向，体现新课程的教学理念.2022 年淮南市、合肥市高三一模不约而同地出现了用“同构”方法解决的问题，检测和培养学生的“数学抽象”等核心素养.

例1（淮南市2022 年高三第一次模拟考试理 科 第12 题）设a=15 ln 13，b=14 ln 14，c=13 ln 15，则（）

A.a＞c＞bB.c＞b＞a

C.b＞a＞cD.a＞b＞c

例2（淮南市2022 年高三第一次模拟考试理科第21 题）已知函数f(x)=

（1）研究函数f(x)的单调性；（2）已知λ＞0，若存在x∈(1,+∞)时，不等式λx2-λx≥(eλx-1)lnx成立，求λ的取值范围.

例3（合肥市2022 年高三第一次教学质量检测理科第12 题）若不等式ex-aln(ax-1)+1≥0，对恒成立（e 为自然对数的底数），则实数a的最大值为（）

A.e+1 B.e C.e2+1 D.e2

2 问题探究

数学抽象是指通过对数量关系与空间形式的抽象，得到数学研究对象的素养，包括从数量关系中抽象出一般规律和结构，并用数学语言予以表征.“同构”是数学对象之间的一类映射，它揭示了这些对象存在的关系.在中学数学日常教学中，如果不等式中出现两个具有相同结构特征的代数式，通俗地称它们为同构式.通过构造函数模型，利用导数研究函数的单调性，将函数值的大小关系，转化为自变量的大小关系，化繁为简，使问题得以顺利解决.

例1 解析比较a=15 ln 13 与c=13 ln 15 的大小简单些，可以转化为比较与的大小，这两个式子结构相同，构造函数f(x)=利用导数知f(x)在(e,+∞)上单调递减，因此，即15 ln 13 ＞13 ln 15.

通过观察a、b、c的形式，直觉b介 于a、c之间.直接比较a与b、b与c大小，依然转化成相同的结构，引入函数解决问题.比较a=15 ln 13 与b=14 ln 14 的大小，可以转化为比较与的大小，构造函数g(x)=，再研究它的单调性，可得a＞b.比较b=14 ln 14 与c=13 ln 15 的大小，可以转化为比较与的大小，构造函数h(x)=再研究它的单调性，可得b＞c.

例2 解析第（1）题，利用导数可知f(x)在区间(0,1)，(1,+∞)上均单调递减.

第（2）题，因为λ＞0，x＞1，

例3 解法1ex-aln(ax-1)+1≥0 ⇔xex+x≥axln(ax-1)⇔xex+x≥(ax-1)ln(ax-1)+ln(ax-1) ①

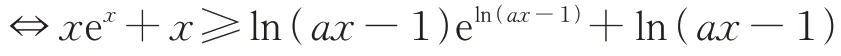
设f(x)=xex+x，利用导数，知f(x) 在上单调递增.

于是由f(x)≥f(ln(ax-1))，得x≥ln(ax-1)，分离参数得a≤

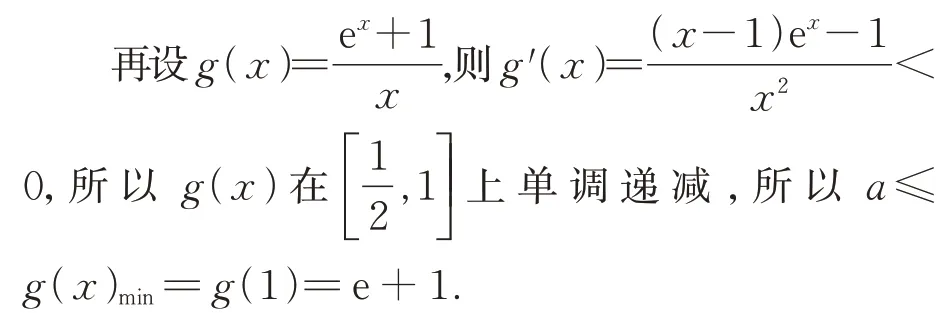
其中代数式恒等变换ax-1=eln(ax-1)是关键.如果用x=ln ex，就得到另外一种解法.

3 问题反思

“同构”的解题意识和技巧是化繁为简、化解难题的有力武器.一方面，“同构”能优化解题思路，简化数学运算，以简驭繁，培养学生创新思维，发展数学核心素养.另一方面，“同构”是数学对称美的体现，是培养学生转化化归思想和数学抽象的重要载体.有些式子结构混搭，需要变形重构，具有相当的灵活性，需要扎实的数学基本功.我们要理解数学知识的本质，关注代数式的结构，做好转化化归，发展数学抽象、逻辑推理等素养.

最后推荐2020 年高考新课标山东卷第21 题，再次说明“同构”思想方法的重要性：已知函数f(x)=aex-1-lnx+lna，（1）略；（2）若f(x)≥1，求a的取值范围.其多样的解法请参见文[2].