函数方程与取整运算的美丽邂逅

江苏省南通开放大学 杨 忠 （邮编：226000）

在化学中，两种物质在一定的条件下遭遇发生化学反应，便有新的物质生成.同样，在数学中，两个不同的知识点碰到一起，也会产生一些新的发现，这样的例子很多，最为经典的例子——坐标系便是代数与几何结合的结果，这个结果对数学的发展产生了深刻的推动作用.笔者这里尝试将函数、方程与取整运算相结合，也有了趣味性发现，这里与同行朋友们分享.

1 函数与取整

1.1 一次函数y=kx+b(k ≠0)

对自变量取整得到函数y=k[x] +b，图象成阶梯形，两个相邻整数之间左闭右开区间上函数值相等，故每一级阶梯宽度为1 个单位；相邻两个整数区间，函数值差为k，故阶梯的高度为直线斜率的绝对值即 ||k，图象夹在一次函数y=kx+b与y=kx+b+1 之间，如图1.

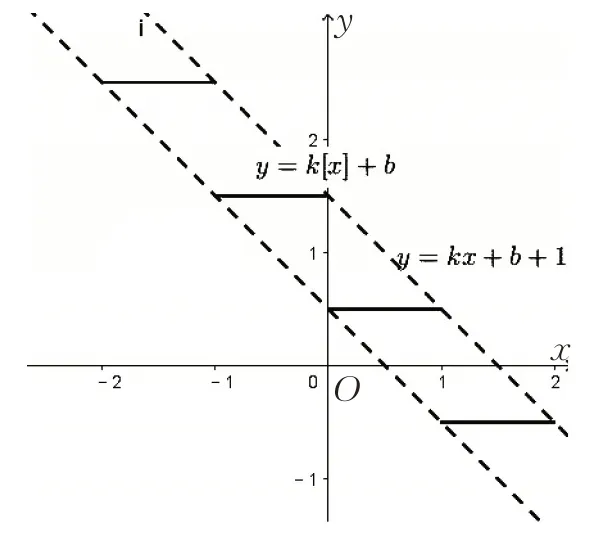
图1

对一次项取整得到函数y=[kx]+b，图象成阶梯形，变量[kx]取值为连续整数值，相邻阶梯的高度为1，[kx]的增量1 由x的增量产生，故每个阶梯的宽度为；图象夹在一次函数y=kx+b与y=kx+b-1 之间，如图2.

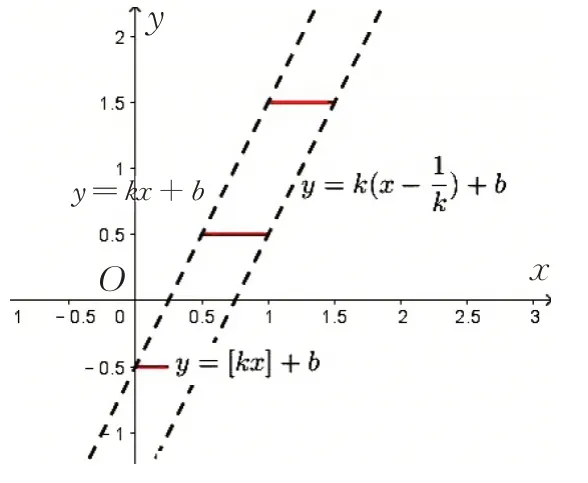
图2

对函数值取整得到函数y=[kx+b]，图象成阶梯形.b=0 时，得到正比例函数的函数值取整y=[kx]，阶梯高度为1，[kx]的增量1 由x的增量产生，每个阶梯的长度为，x轴上区间是图象中离原点最近的一个阶梯.y=则可由y=[kx]图象平移得到，图象夹在y=kx+b与y=kx+b-1 两个函数图象之间，如图3.

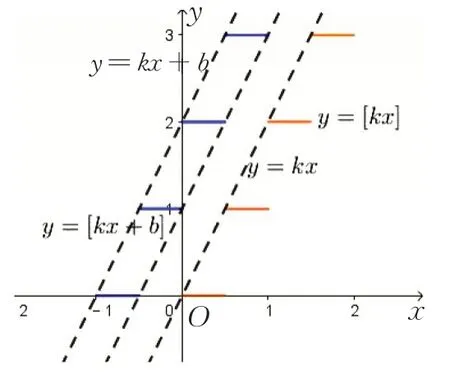
图3

1.2 反比例函数y=

对自变量取整得到函数y=，图象成阶梯形，区间[0,1) 内函数无定义，故无对应的阶梯.其余相邻两个整数构成的左闭右开区间上的函数值相等，故对应的该级阶梯宽度为1 个单位；变量x的绝对值越大，阶梯的高度差越小.图象夹在y=与y=两个函数图象之间，如图4.

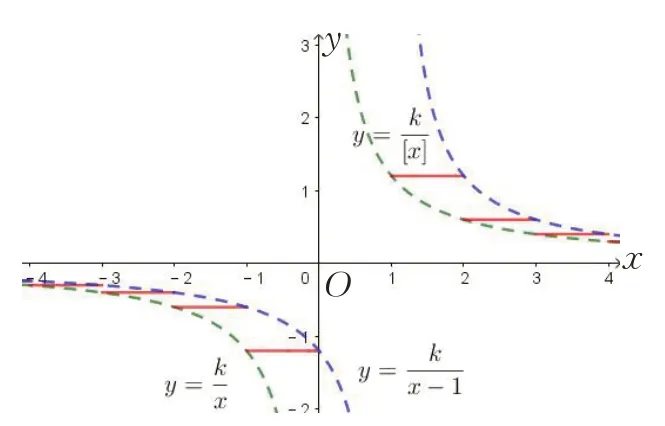
图4

对函数值取整得到函数y=，图象成阶梯形，变量取值为连续整数值，相邻阶梯的高度差为1；变量x的绝对值越大，阶梯的宽度越大，图象夹在函数y=与y=-1 两个函数图象之间，如图5.

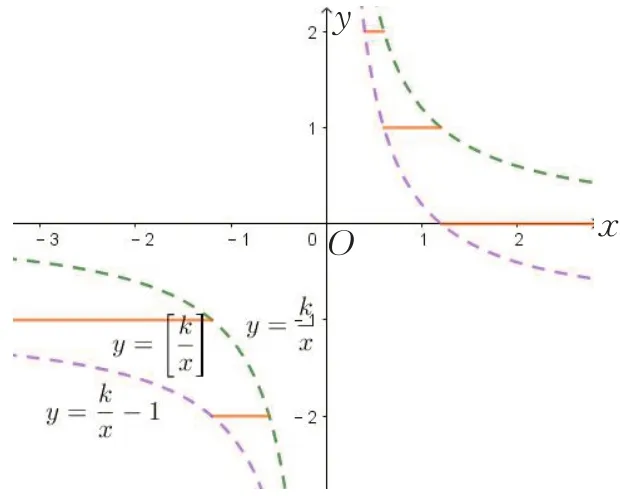
图5

从特殊到一般，从上述特例中可以归纳函数中进行取整运算的图象规律如下：

归纳1如图6，对函数y=f(x) 自变量取整得到y=f([x])，图象成阶梯形，相邻两个整数构成的左闭右开区间内若有定义，则函数值相等，对应的图象即为宽度1 的阶梯.y=f([x])的图象夹在函数y=f(x)与y=f(x-1)两个函数图象之间.

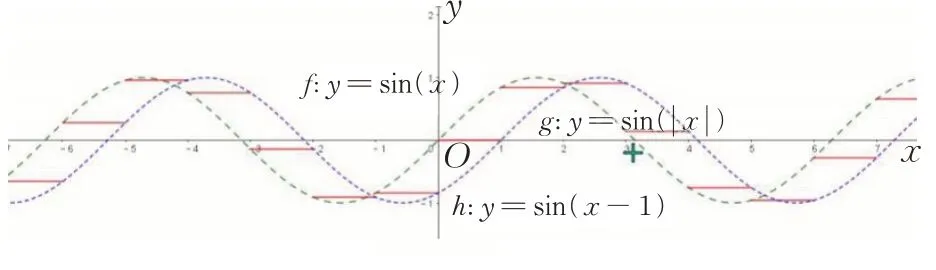
图6

归纳2如图7，对y=f(x)函数值取整得到y=[f(x)]，图象成阶梯形，阶梯高度差为1，y=[f(x)]的图象夹在函数y=f(x)与y=f(x)-1 两个函数图象之间.

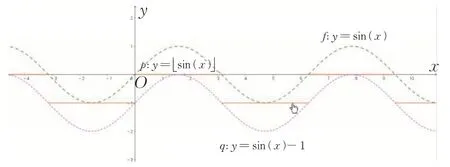
图7

2 方程与取整

2.1 二元一次方程取整

以直线方程2x+3y=6 为例，对二元一次方程的两个变量取整：2[x]+3[y]=6，则[x]、[y]均为整数，取值如下表，

_____________________[_]x 6______9___[]y…________________________________________________________________________________________…_____3__________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________0_____-2___-4____12_____-6____… ___________________________________…__

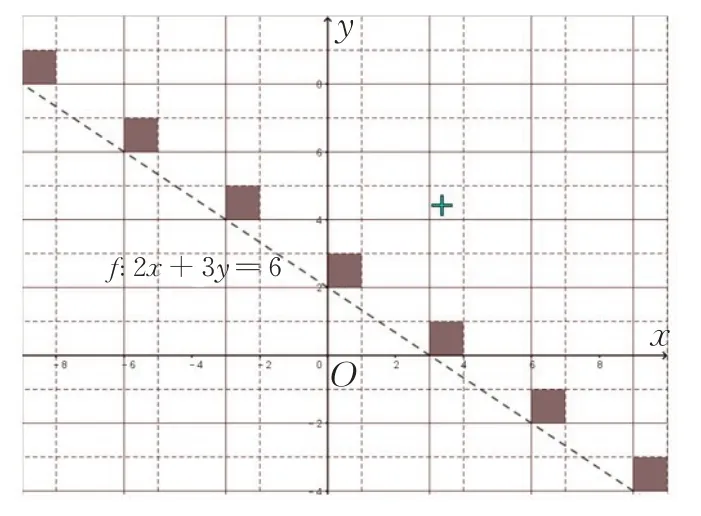
图8

对二元一次方程的两个一次项取整得[2x]+[3y]=6，[2x]、[3y]均为整数，可以取连续整数，

___[]2x___[]3y… _______________________________________________________________________________________…_____1 __________________________________________________________________________________________________5______2 _______________________________________________________________________________________________4_____3 __________________________________________________________________________________________________________3______4 ______________________________________________________________________________________________2_____… ___________________________________…__

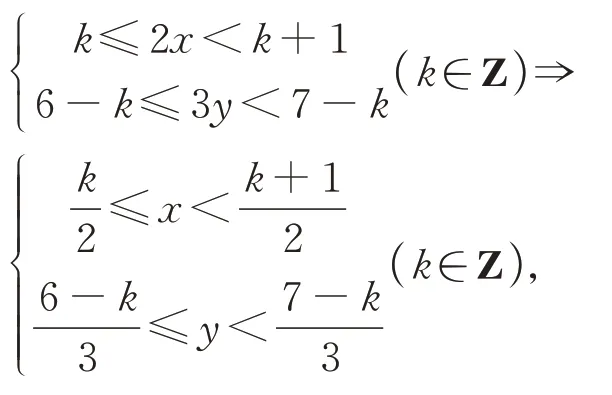
对应的图象应为左下角顶点在直线2x+3y=6 上的相连矩形块（不含右边框与上边框）如图9.

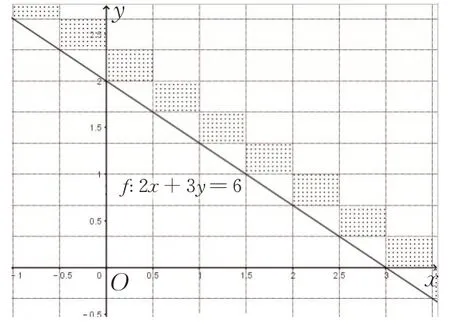
图9

对二元一次方程的含变量部分取整得[2x+3y]=6，应有6 ≤2x+3y＜7，函数图象如图10 .

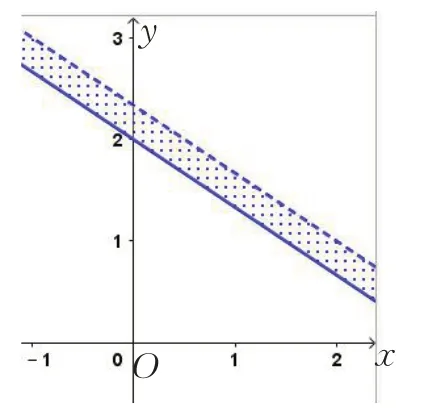
图10

2.2 圆方程取整

以圆方程x2+y2=25 为例，对二元一次方程的两个变量取整得到方程：[x]2+[y]2=25，由[x]、[y]均为整数，取值如下表，

[_]x______0______3_____4[]y 0_____________________________________________________________________________________________________________5_-___5 3___________________________________________________________________________________________________________________4__-4__4____________________________________________________________________________________________________________3_-3_5 __________________________0___-5 0___-4_3__-4_-3___-3 4__-3-4

以得到方程2[x]+3[y]=6 图象的类似方法，可以得到图象为圆x2+y2=25 上整点为左下角顶点的单位正方形（不含右边框与上边框）组成的区域，如图11.

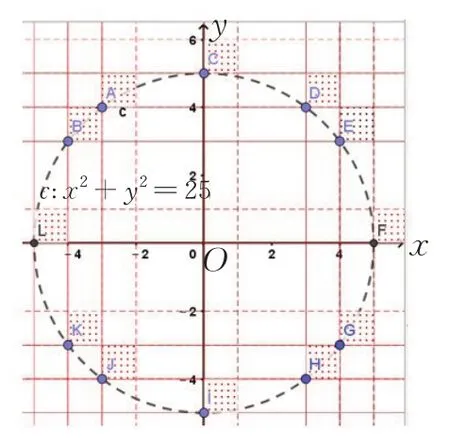
图11

以圆方程x2+y2=10 为例，对二元一次方程的两个二次项取整得到方程得[x2]+[y2]=10，由[x2]，[y2]均为整数可得：

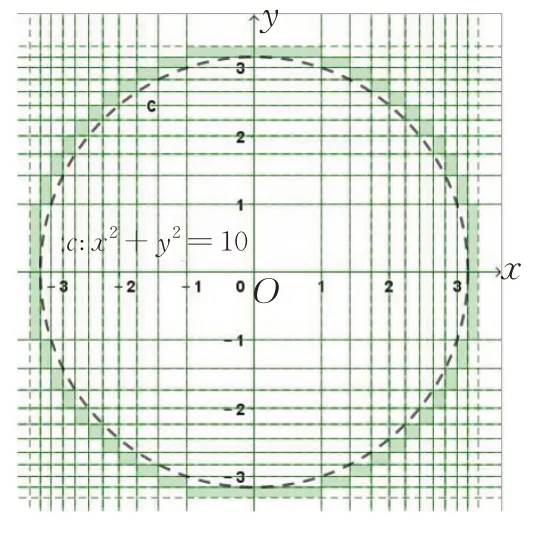
图12

若对圆方程x2+y2=10 的含变量部分取整：[x2+y2]=10，则 有10 ≤x2+y2＜11，对应图象为不含外边框的圆环.

从上述特例中可以归纳方程中进行取整运算的图象规律如下：

归纳3对二元方程的两个变量分别取整，则图象由左下角顶点为原方程图象上的整点，不含右边框与上边框的所有单位边长正方形所组成的区域.

归纳4对直线方程的一次项取整，图象位于在原方程直线上方，左下角顶点在原方程直线上且相互连接的矩形串（不含右边框与上边框）；对圆的标准方程中二次项取整，图象为在原方程图象外侧、一个顶点在原方程曲线上且相互连接的矩形串（不含右边框与上边框）.

3 规律应用

例1记[x]表示不超过实数x的最大整数.设R 是满足的点(x,y)构成的区域.则区域R 的面积为__________.

解析先考虑等式[x]+[y]=7，由[x]，[y]为整数，再由x≥0，y≥0，[x]、[y]均为整数，取值如下表：

__[______]x__[]y 0 ________________________________________________________________________________7_____1 _______________________________________________________________________________6_____2 _______________________________________________________________________________5_____3 _______________________________________________________________________________4_____4 _______________________________________________________________________________3_____5 _______________________________________________________________________________2_____6 _______________________________________________________________________________1_____7 ______________________________________0__

如图13，区域R 由8 个单位正方形组成，面积为8.

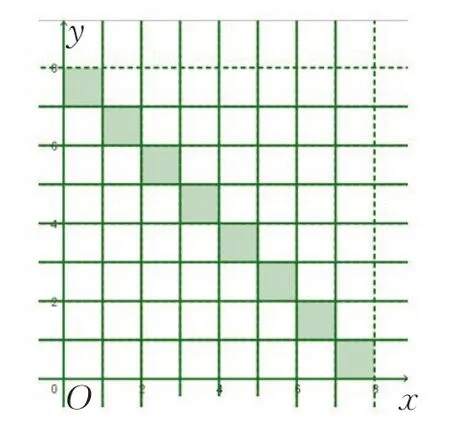
图13

例2（《中等数学》2021 年5 期数学奥林匹克训练题）记[x]表示不超过实数x的最大整数.设R 是满足的点(x,y)构成的区域.则区域R 的面积为________.

解析寻找区域的临界，故先考虑等式x+y+[x]+[y]=7，即{x}+{y}+2[x]+2[y]=7，故 {x}+{y}为 整 数，而 0 ≤{x}＜1，0 ≤{y}＜1，故0 ≤{x}+{y}＜2，所 以{x}+{y}=1，[x]+[y]=3，故x+y+[x]+[y]=7等价于x+y=4.x+y+[x]+[y]≤7，即x+y≤4，故满足的点(x,y)构成的区域R 的面积为8.

例3设记[a]表示不超过实数a的最大整数，实数x、y满足[x]2+[y]2≤10，求2x+3y的最小值.

解析由[x]2+[y]2≤10，[x]2、[y]2为 完全平方数得下表：

__x2[_]y 2[]__1 ___________________________________________9__9 ___________________________________________1__0 ___________________________________________9__9 ___________________________________________0__4 ___________________________________________4__1 ___________________________________________4__4 ___________________________________________1__0 ___________________________________________4__4 ___________________________________________0__1 ___________________________________________1__0 ___________________________________________1__1 ___________________________________________0__0 0

[x]2+[y]2≤10 对应的区域，如图14，其左边沿与下边沿包括在区域内部，为实线；其右边沿与上边沿不包括在区域内部，为虚线.

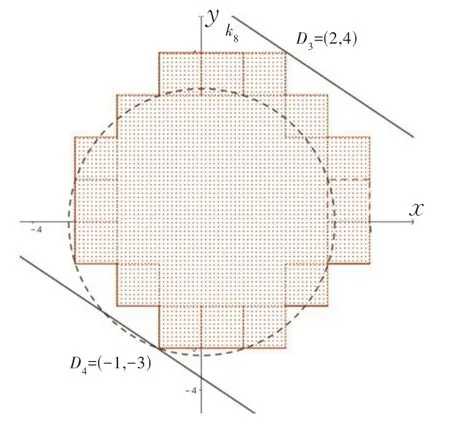
图14

记2x+3y=t，则直线2x+3y=t经过点(-1,-3)、(2,4)时，得到t的范围为[ -11,16)，故2x+3y的最小值-11.