和谐两定理 共解高考题
2022-04-26陕西省西安市高新第三中学吕二动邮编710075
陕西省西安市高新第三中学 吕二动 (邮编:710075)
1 定理展现
三余弦定理(又叫最小角定理)
如图1 所示,设A为面α上一点,过A的斜线AO在面α上的射影为AB,AC为面α内的一条直线,那么∠OAC,∠OAB,∠BAC三角的余弦关系为:

图1
cos ∠OAC=cos ∠BAC·cos ∠OAB.(∠BAC和∠OAB只能是锐角)
证如上图,自点O作OB⊥AB于点B,过B作BC⊥AC于C,边OC,则 易 知△OAC、△ABC、△OAB均为直角三角形.
令∠OAB=θ1,∠BAC=θ2,∠OAC=θ,
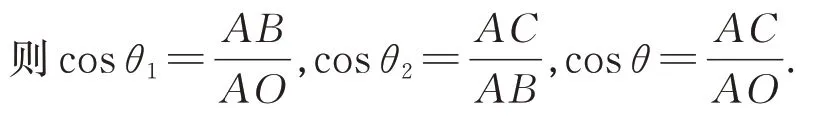
所以cosθ=cosθ1·cosθ2.
辅助记忆这三个角中,角θ是最大的,其余弦值最小,等于另外两个角的余弦值之积.斜线与平面所成角θ1是斜线与平面内所有直线所成的角中最小的角.
通俗点说就是,斜线与平面内一条直线夹角θ的余弦值=斜线与平面所成角θ1的余弦值×射影与平面内直线夹角的余弦值.特别地,当∠BAC为零角时,由于cos 0=1,所以斜线与射影所成的角是斜线与平面内的任何直线所成的角中的最小的角.
三正弦定理设二面角M-AB-N的度数为α,在平面M上有一条射线AC,它和棱AB所成角为β,和平面N所成的角为γ,则sinγ=sinα·sinβ(如图2)

图2
证 明如 图2,过C作CO⊥平面N于点O,过O作直线OB⊥二面角的棱于点B,连OA、CB,则易知△CAO、△CBO、△ABC均为直角三角形.于是sinγ=sinα=sinβ=所以sinγ=sinα·sinβ.
2 定理应用
例1在RtΔABC中,∠A=AB=3,AC=4,PA是面ABC的斜线,∠PAB=∠PAC=
(1)求PA与面ABC所成的角的大小;
(2)当PA的长度等于多少时,点P在平面ABC内的射影恰好落在边BC上?
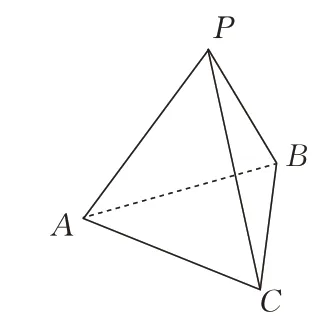
图3
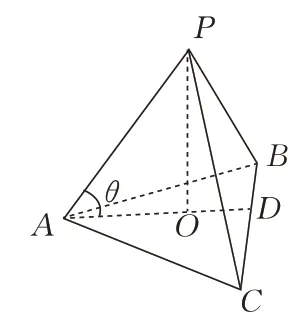
图4
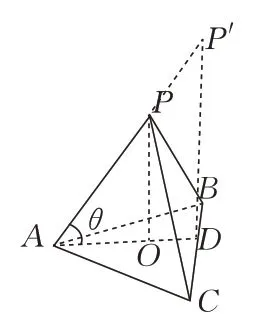
图5

因为直角三角形ABC的直角平分线长AD,所以当延长AP到P′时,AD成为斜线AP′的射影,垂足D恰好落在边BC上,所以AP′=,即当PA的长度等于时,点P在平面ABC内的射影恰好落在边BC上.
例2(1994 年全国高考理科数学23 题) 如图6,已知A1B1C1-ABC是正三棱柱,D是AC中点.
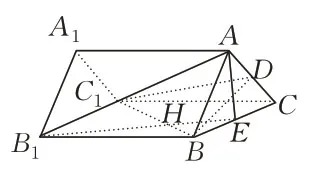
图6
(1)证明:AB1∥平面DBC1;
(2)假设AB1⊥BC1,求以BC1为棱,DBC1与CBC1为面的二面角α的度数.
(1)证明因为A1B1C1-ABC是正三棱柱,所以四边形B1BCC1是矩形.连结B1C交BC1于E,则B1E=EC,连结DE.
在△AB1C中,因AD=DC,所以DE∥AB1.
又AB1⊄平面DBC1,DE⊂平面DBC1,所以AB1∥平面DBC1.
(2)解取BC中点E,连结B1E、AE,则B1E是AB1在平面B1BCC1上的射影.
由AB1⊥BC1可得EB1⊥BC1,设垂足为H,BC=2a,在Rt△BB1E中BE2=EH·EB1,

所以α=450,故二面角α为45°.
例3(2019 年全国1 卷)已知∠ACB=90°,P为平面ABC外 一点,PC=2,点P到∠ACB两边AC、BC的距离均为那么P到平面ABC的距离为________.
解析如图7 由对称性知∠COD=450,由三余弦定理 得cos ∠PCD=cos ∠PCO·cos ∠OCD,即cos ∠PCO=所以PO=OC=
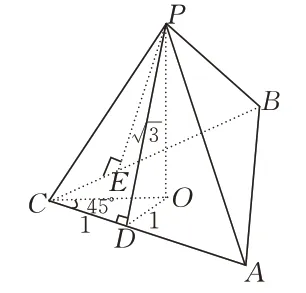
图7
例4(2017 年全国3 卷)a、b为空间中两条互相垂直的直线,等腰直角三角形ABC的直角边AC所 在直线与a、b都垂 直,斜边AB以直 线AC为旋转轴旋转,有以下列结论:
①当直线AB与a成60°角 时,AB与b成30°角;
②当直线AB与a成60°角 时,AB与b成60°角;
③直线AB与a所成角的最小值为45°;
④直线AB与a所成角的最大值为60°.
其中正确的是________(填写所有正确结论的编号)
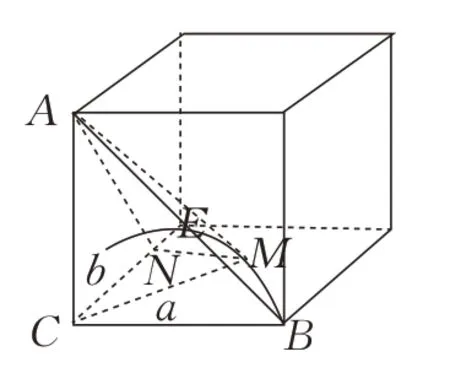
图8
解析过点M作b的垂线,则AM与AN所成的角为AM与a所 成的角,由三余弦定理得cos ∠AMN=cos ∠AMC·cos ∠CMN=cos ∠CMN,若所成角为60°,则有cos ∠CMN,则cos ∠CMN=450,CM平分角∠BCE,所以AM与两直线所成的角都是60°,故②正确,由图可知③显然成立,所以正确是②③.
3 跟踪训练
例4(上海市1986 年高考试题) 已知Rt△ABC的两直角边AC=2,BC=3.P为斜边AB上一点,现沿CP将此直角三角形折成直二面角A-CP-B(如图9),当AB=时,求二面角P-AC-B的正弦值.
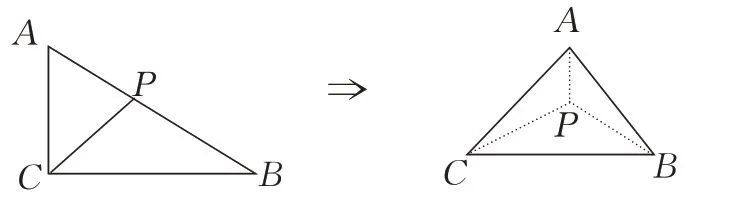
图9
解析设二面角P-AC-B的大小为α.

例5已知菱形ABCD的边长为1,∠BAD=60°,现沿对角线BD将此菱形折成直二面角A-BD-C.

图10
(1)求异面直线AC与BD所成的角;(2)求二面角A-CD-B的正弦值.
解析设二面角二面角A-CD-B的大小为α.易证AO⊥面BDC,且△AOC为等腰直角三角形,所以∠ACO=450,又知∠DCO=300,
由三余弦定理得cos ∠ACD=cos ∠ACO·cos ∠DCO,即cos ∠ACD=cos 450·cos 300=所以sin ∠ACD=
由三正弦定理,得sin ∠ACO=sin ∠ACD·sinα,解得sinα=
