错在哪里

1 江苏省东海高级中学

冯维清（邮编：222300）

题目如图1，在△ABC中，AC＞AB，cosA=AB=8.若c os(B-C)=，求S△ABC.

图1

错解因为AC＞AB，所以∠B＞∠C，在AC边上取一点D，使DB=DC，

解答错了！错在哪里？

在△ABD中，AB=8，AD=4BD，以线段AB所在直线 为x轴，AB的 垂直平分线为y轴建立平面直角坐标系，由阿波罗尼斯圆定义可知，D点的轨迹是靠近B点的一个圆C，圆方程为(x-)2+y2=如图2，若利用cosA=求解，可得两解，△ABD与△ABD′都符合，又cos ∠ABD=所以△ABD′不合题意，故S△ABC=

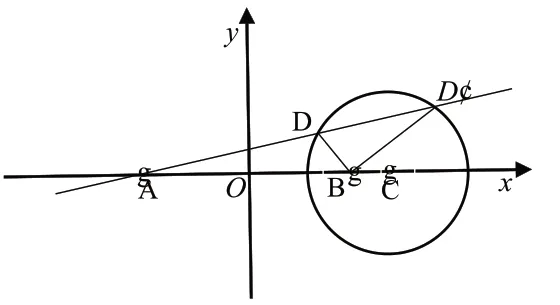
图2

正确解答

解法一在△ABD中，因D点的轨迹是靠近B点的一个圆C，故利用

2 安徽省安庆市第二中学

王 庆（邮编：246001）

题目已知四个实数成等比数列，乘积为1，第2 项与第3 项和为-，则该数列为_____.

解答设四个数为由题意得.解①得a4=1，所以a2=1，整理②得2aq2+3q+2a=0，Δ=32-4×2a×2a=3-16a2，a2=1 代 入Δ=-13 ＜0，方程组无实数解，数列不存在.

解答错了！错在哪里？

错因分析解决等差数列和等比数列时，经常用对称设项法解题.该方法比基本量法更简洁.但是在等比数列中，如果是三项，设为aq解题没有问题.如果是四项时，设为aq3，公比为q2＞0.因此，所设四项时同号，解题是收到限制.如果四项不知道是否同号，只能用基本量法求解.

正确解法

总结解决本小题三个关键点：一是注意设项方法，二是处理②式平方简化了运算量，三是求出q后求a，选择哪个方程代入有讲究.a2=是平方后得到的结果，所以容易产生增根.在学习中对于方法使用题型和条件需要分析、理解，不能盲目套用.