直驱H型平台的Laguerre迭代轮廓控制研究*

魏惠芳，王丽梅

(沈阳工业大学电气工程学院，沈阳 110870)

0 引言

直驱H型平台具有响应速度快、正交精度高和可靠性强的优点，被广泛应用于各类高精度工业制造中。在直驱H型平台三轴协同运动中，由于各坐标轴动态特性存在差异，单纯从单轴伺服控制的角度无法彻底解决加工过程中的轮廓跟踪精度问题[1]。因此，建立精确的轮廓误差模型，设计合理的控制策略，对于提高直驱H型平台的轮廓跟踪精度具有重要意义[2]。

为提高直驱H型平台的轮廓跟踪精度，学者们通常从建立精准的轮廓误差模型和选择适合的轮廓控制方法两方面来研究。张宝林等[3]设计了一种实时轮廓误差估计方法，通过确定规则轮廓误差点的方式，提高了系统的轮廓精度，但其仅考虑简单的线性或圆形轮廓，无法保证大曲率复杂轮廓的跟踪精度。陈阳等[4]设计了基于轮廓最优圆逼近的轮廓误差估计模型，实现了对复杂加工过程轮廓误差的实时估算和补偿。然而，精准的轮廓误差模型固然可以提高系统的轮廓跟踪精度，但还需结合适合的轮廓控制方法才能效果显著[5]。

迭代学习控制在重复运动控制中得到了广泛的应用[6]。迭代学习控制中求解多项式的根可以采用牛顿迭代法、弦截法及多重迭代法，但这些方法对于初始近似值要求较高。ZHANG等[7]为了减少扰动项引入的分裂误差，优化了基于Laguerre法的时域有限差分迭代算法，通过改进算法，进一步加快了系统的收敛速度。许鸣吉等[8]将迭代交叉耦合控制器应用到三轴直角坐标机器人末端执行器位姿精度的控制系统中，从而克服系统机械惯性、负载扰动以及复杂的轮廓误差模型等因素的影响。

为提高直驱H型平台在跟踪高速大曲率复杂轮廓时的轮廓加工精度，本文提出一种基于精密轮廓误差模型的Laguerre迭代轮廓控制方法。首先，采用有理多项式求根方法建立适用于大曲率高速运动的直驱H型平台轮廓误差模型，克服了轮廓误差其它估计方法估计条件受限、估值不准确等问题；其次，采用Laguerre迭代方法，该学习控制方法较比牛顿方法在迭代过程中体现得更快和更强的收敛性，在轮廓误差建模的基础上设计了基于拉盖尔迭代的交叉耦合控制器，解决了大曲率，复杂路况下轮廓误差减小不显著的问题；最后，通过实验验证该方法的可行性和有效性。

1 直驱H型平台高精度实时轮廓分析

直驱H型平台模型示意图如图1所示。该实验平台由H型连接的滚珠丝杠直线导轨支撑三台PMLSM做高速、高精度平面运动。

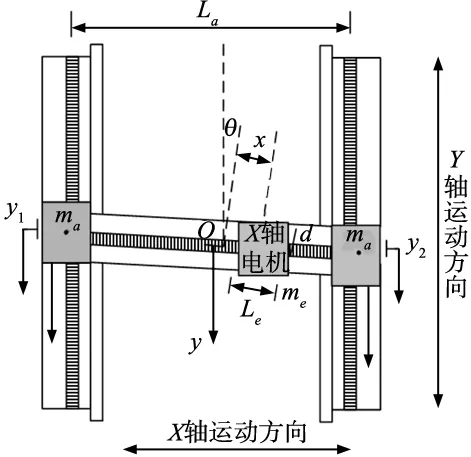
图1 直驱H型平台模型示意图

图1中，y1、y2为平行轴的实际位置；y为工作台在Y轴方向的实际位置；La为横梁长度；θ为横梁与水平位置夹角；x为工作台到横梁中点的距离(此处忽略了扭转引起的横梁的水平误差)；横梁质量ma(包括Y轴电机动子)和X轴滑动物块质量me；d为滑动物块到横梁中心线的垂直距离；Le为横梁上滑动物块的长度。

平台三轴协同运动中，当轨迹曲率较大且变化速度快时，负载实际位置p(xp,yp)与当前参考点r(s)存在显著差异时，不满足密切圆估计条件，不能使用密切圆近似估计轮廓误差[9]。

假设路径r(s)=(x(s),y(s))是一个多项式有理式曲线，定义s∈[0,1]。结合实际位置p(xp,yp)，可得任何给定时刻的轮廓误差为[10]：

(1)

(2)

令式(2)等于零，其中si,...,sN是s∈(0,1)上的多重根，将式(2)的分子作为考虑的对象，定义

G(xp,yp,s)=[xp-x(s)]x′(s)+[yp-y(s)]y′(s)

(3)

设s0=0且sN+1=1。由于对G(xp,yp,s)整体的考虑过于复杂，因此观察式(3)可发现，当r(s)是n次有理曲线时，G(xp,yp,s)也可以被简化为s(或更高次)的多项式；如果r(s)是样条曲线，那么G(xp,yp,s)就可以被简化为s的样条函数。因此，只需分析多项式曲线r(s)的情况即可。

式(3)的实根表示r(s)的点，其中p位于曲线的法线上。由于

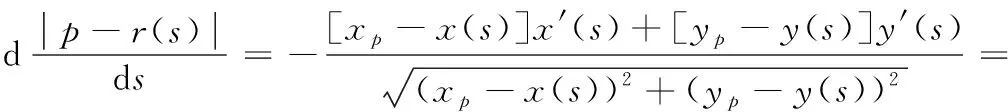
(4)

因此，|p-r(s)|的值在si,...,sN处达到局部平稳值。由于式(3)的多重根为偶数表示|p-r(s)|的值是平稳的，但不是极值，因此只考虑式(3)的根为奇数的情况。|p-r(s)|的值是内部极值距离中最小的，到端点r(0)和r(1)的距离也是最小的。为区分|p-r(s)|的极小值和极大值，将其二阶导数写为：

(5)

式中，

G′(xp,yp,s)=[xp-x(s)]x′′(s)+
[yp-y(s)]y′′(s)-x′2(s)-y′2(s)

(6)

由于G(xp,yp,s)=[xp-x(s)]x′(s)+[yp-y(s)]y′(s)=0对于i=1,...,N，如果si是|p-r(s)|的最小值，它的二阶导数为正，如果G′(xp,yp,s)<0，则有

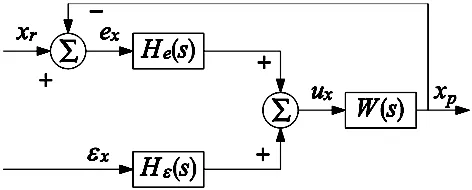
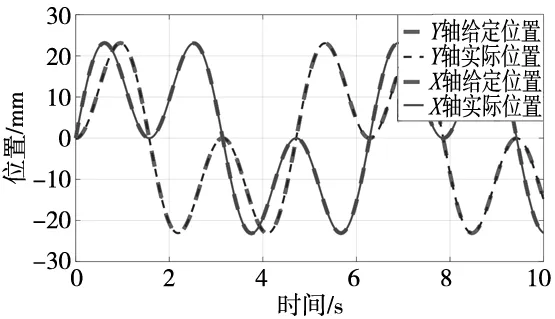
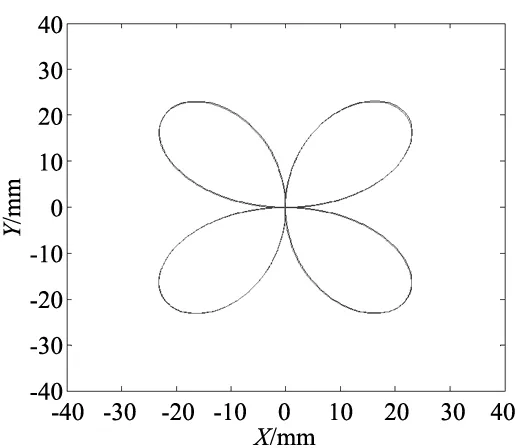
[xp-x(s)]x′′(s)+[yp-y(s)]y′′(s)

(7)

当式(1)中的最小值为i=m时，称r(sm)为曲线r(s)上p的一个足点，如果1≤m≤N，则r(sm)为一个内部足点，如果m=0或N+1，则r(sm)为一个终端足点。通常，足点是唯一的，但对于p(xp,yp)的某些特殊位置，可能有多个足点。

对于p(xp,yp)的一般位置，当p(xp,yp)相对于曲线移动时，实现式(1)中最小值的根的“恒等式”保持不变，在那个位置附近，对邻域内p(xp,yp)的位置有解析依赖关系。因此，当p(xp,yp)移动时，sm的值可以通过数值解析方法来更新。但是，当p(xp,yp)经过某些关键位置时，式(1)中最小值的根的恒等式可能会发生变化，不能通过解析来更新。

(1)当p(xp,yp)在s=0或1处越过法线到达r(s)时，s∈[0,1]上从s<0或s>1处出现或消失一个式(2)的实根；

(2)p(xp,yp)的位置与当前足点的曲率中心重合，通过复共轭根对的出现或消失，导致式(2)的实根数发生变化；

(3)p(xp,yp)的位置可能有非唯一的足点，这些点是式(1)中的最小值由式(2)的至少两个不同的实根si,sj∈[0,1]和|p-r(si)|=|p-r(sj)|实现的。

2 基于Laguerre迭代的轮廓跟踪控制

不断跟踪G(xp,yp,s)所有根的方法虽然简单但效率较低，为提高效率采用适当的迭代方法进行估计并实时控制。当p从某个初始点pa=(xa,ya)以离散的步骤Δp移动时，为了跟踪式(2)的所有根s1,…,s2n-1，需要这些根的初始值。当p=pa时，需要确定多项式的所有根。

Q(s)=G(xa,ya,s)

(8)

将式(8)的每个根隔离在一个复平面矩形内，基于“参数原理”和Sturm序列计算复矩形中根的数量。

一旦式(8)的根被充分隔离，就可以调用迭代方法来确定每个根的精度，使用矩形中心作为起始值。因为Laguerre迭代比牛顿迭代方法显示更快和更强的收敛性[10]。Laguerre迭代的定义为：

(9)

列g(s)=(m-1)[(m-1)f′2(s)-mf(s)f′′(s)]，选择式(9)以使|s(r+1)-s(r)|最小化。虽然Laguerre方法也使用f(s)的二阶导数和平方根提取，但与牛顿方迭代法相比，收敛速度和收敛精度极大提高。

使用Laguerre的方法来更新根，将G(xp+Δxp,yp+Δyp,s)标识为f(s)，并将G(xp,yp,s)的收敛根作为Laguerre迭代的初始值。通常，Laguerre方法会在一两次迭代中收敛到适当大小的步骤Δp的机器精度。一旦知道与p+Δp对应的根，对s∈(0,1)和s=0,1上的每个实根求|p+Δp-r(s)|的值，即为最小的值，然后决定距离(p+Δp,r(s))。

知道足点参数值sm，轮廓误差向量可以定义为ε=r(sm)-p。其中，ε是一个非负的数量，可以把它和n·ε的符号联系起来把它转换成带符号的量，n是足点r(sm)处的法线。

图2为X轴的交叉耦合控制方案。控制信号ux通过轴向动力学传递函数W(s)确定实际位置xp。X轴位置误差为轴编码器测量的参考位置xr与实际位置xp的差，即ex=xr-xp。εx为轮廓误差矢量的X轴分量。He(s)为PI控制器，取Hε(s)为He(s)的比例函数。

图2 X轴交叉耦合控制框图

3 系统实验分析

图3 实验系统结构图

为验证基于Laguerre迭代轮廓误差估计方法对提高直驱H型平台轮廓跟踪精度的有效性，选用型号为BJSM-X360-Y360的直驱H型平台。实验平台如图3所示，整个系统包含PC机、H型运动平台、运动控制箱等。此外，实验中所用直驱H型平台基本参数为：ma=8.3 kg，me=10 kg，La=0.700 m，Le=0.350 m，选取交叉耦合控制，交叉耦合控制增益为0.2，选取总迭代次数为50次。

在实验时，在拖动100 N负载的条件下对直驱H型平台输入大曲率的四叶草轮廓曲线，其中X轴输入信号为rx=60sintcos2t，Y轴输入信号为ry=60sin2tcost。为了验证所提控制方法的有效性，采用基于牛顿迭代的轮廓误差估计方法进行对比。

图4和图8分别为采用牛顿迭代和Laguerre迭代轮廓估计误差方法下的直驱H型平台的轮廓跟踪曲线，并且在图5和图9中给出两种方法控制下的轮廓误差曲线。对比两图可以看出，采用牛顿迭代学习下的轮廓误差约为-4.2～4.2 μm之间波动，而采用本文设计的Laguerre迭代轮廓误差估计方法的误差约为-1.8～2.1 μm，明显提高了轮廓跟踪精度。这表明，在如四叶草轮廓的大曲率路径下，采用Laguerre迭代轮廓误差估计方法能够有效提高减小轮廓误差。

此外，为分析该方法对于单轴跟踪误差的有效性，在图6和图7中给出采用牛顿迭代轮廓误差估计方法下的X轴和Y轴位置响应曲线，在图10和图11中给出采用本文设计的Laguerre迭代轮廓误差估计方法控制下的单轴位置响应曲线。观察图7可以看出，采用牛顿迭代学习的X轴和Y轴位置跟踪误差约为-9.5～9.5 μm。而从图11中可发现，两轴的位置跟踪误差分别减小到-5.1～4.8 μm。这表明，本文设计的轮廓误差估计方法对于提高单轴位置跟踪精度也具有一定的有效性。因此，通过以上实验分析可以得出，基于精确轮廓误差估计的直驱H型平台Laguerre迭代控制方法具有较好的收敛性，对于提高轮廓加工精度有一定的意义。

图4 基于牛顿迭代轮廓误差估计方法的轮廓跟踪曲线

图5 基于牛顿迭代轮廓误差估计的轮廓误差曲线

图6 基于牛顿迭代轮廓误差估计的单轴位置响应曲线

图7 基于牛顿迭代轮廓误差估计的位置跟踪误差曲线

图8 基于Laguerre迭代轮廓误差估计方法的轮廓跟踪曲线

图9 基于Laguerre迭代轮廓误差估计的轮廓误差曲线曲线

图10 基于Laguerre迭代轮廓误差估计的单轴位置响应曲线

图11 基于Laguerre迭代轮廓误差估计的位置跟踪误差曲线

4 结论

为实现直驱H型运动平台的高精度轮廓控制，提出一种基于精确轮廓误差估计的Laguerre迭代控制方法。针对高速大曲率轮廓轨迹，通过有理多项式求根方法建立精准的轮廓误差估计模型。在此基础上，设计Laguerre迭代与交叉耦合相结合的轮廓控制方法，实现三轴之间的协同控制，从而提高系统的轮廓精度。实验结果验证了该控制方法对于提高直驱H型平台轮廓加工精度的有效性。