基于粒子群算法的装配公差组合优化*

2022-04-26唐秋华魏国前

组合机床与自动化加工技术 2022年4期

秦桢，唐秋华，魏国前，孙伟

(武汉科技大学a.冶金装备及其控制教育部重点实验室；b.机械传动与制造工程湖北省重点实验室，武汉 430081)

0 引言

在装配时装配体末端的功能要求，须由各个装配特征参数联合保证[1]。各参数的组合形式不同，最终装配体性能差异可能会很大。对于精度要求较高的机构，在设计初期亟需对装配特征参数进行优化，通过合理的公差分配，既降低产品制造成本，又保证装配体的精度。

针对装配公差设计，王辉等[2]构建了雅克比旋量模型，进行了基于公差原则的装配公差统计分析，考虑了不同公差原则下装配体末端公差的范围；PENG等[3]基于雅可比旋量模型，提出以统计学原理来解决机械装配体的三维公差重新设计的新方法。高瑞等[4]在满足整体装配质量的前提下，利用中间计算法优化零件尺寸公差，从而提高了零件合格率。赵帅帅等[5]构建了成本公差函数，提出了基于群智能算法的中间轴公差优化设计方法。周钊等[6]提出了一种基于布谷鸟算法的多目标公差设计方法。

上述三维公差分析方法，大多基于蒙特卡洛仿真，对某种装配特征参数进行公差分析，而对多种装配特征参数组合优化的考虑较少；其次，他们只获得装配误差的概率分布曲线，未计算公差上下区间的最大边界值，导致优化计算时工作量较大，计算结果的鲁棒性较差。为此，提出一种雅克比矩阵旋量最值模型，以此获得装配体末端的公差最大分布区间；再利用各个装配特征参数的联合优化，得到给定条件下的最优公差参数组合。

1 问题描述和求解思路

本问题可描述为在不考虑其它因素对装配体末端误差影响的前提下，对各个装配特征参数进行联合优化，以提高末端装配精度。下面以手术时用于安全分离肿瘤和脑组织的脑神经外科手术机器人为例，描述装配公差优化问题。该机器人结构简图如图1所示，共有6个自由度。

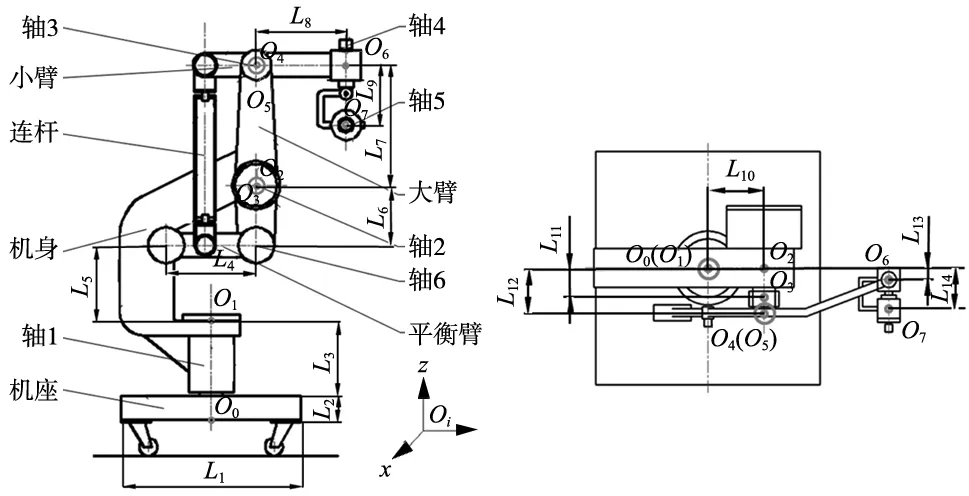
(a) 主视图 (b) 俯视图

在图1中O0是全局坐标系，Oi是装配特征的参考坐标系；Li为各个坐标系的相对位置，L1～L14分别为{600、90、300、300、400、200、400、300、200、100、60、100、10、90}，单位是mm。轴1连接机座，整个机构主要通过轴1→机身→轴2→大臂→轴3→小臂→轴4传递力和力矩，连杆和平衡臂起辅助作用。故而，所建立的装配公差优化模型着重考虑上述传递路径上的装配特征，包括轴1的圆柱度、轴2的圆柱度、O3处大臂孔轴线以大臂外表面为基准的平行度、O4处小臂孔轴线以小臂外表面为基准的平行度、O5处大臂孔的中心线基于大臂端面的垂直度、O6处小臂孔的中心线基于小臂端面的垂直度。

对该问题的主要求解思路是，建立各装配特征的雅可比旋量模型；通过对该模型改进，得到雅克比旋量最值模型，推导出装配体末端公差最大分布区间的计算公式。在此基础上，优化装配特征参数，找到使末端公差分布最大区间最小化的参数组合，亦即装配体末端装配精度最高。

2 公差优化数学模型

在公差计算时，若能知道公差变动区间的边界，并以此为约束，即可简化问题求解。为此，本节提出基于雅克比旋量最值模型的装配体末端误差分布区间求解方法。该方法首先建立装配特征的小位移旋量模型，确定每个装配特征平动矢量的上下限；其次通过对旋量表达式进行分析，获得误差极限；最后，构建雅克比旋量最值模型，计算装配体的末端误差分布区间，找到使末端误差最小的装配参数组合。

2.1 雅克比旋量模型

雅克比旋量模型以机器人运动学、计算机图形学和旋量理论为基础，通过空间尺寸链的误差传递，建立最终功能要求与各装配特征之间的数学关系，从而为装配体公差分析提供数学依据。具体模型如下：

(1)

式中，FR表示功能要求；JFEi表示第i个装配特征的雅克比矩阵；τFEi表示第i个装配特征的小位移旋量；n表示对末端误差有影响的装配特征数量。

(2)

(3)

(4)

装配体中包含多种装配特征，这里以轴1圆柱度为例，建立其公差数学模型[9]：

(5)

式中，l是圆柱的长度；TL是圆柱直径尺寸的下偏差的绝对值；TU是圆柱直径尺寸的上偏差的绝对值；Tcyl是圆柱度的公差值；x、y、z是圆柱度公差带的边界坐标；θ和d表示对应的平动矢量和转动矢量。

2.2 雅克比旋量最值模型

雅克比旋量模型结合了雅克比矩阵和小位移旋量，可用于表征误差的传递与累积[7-8]。但是，小位移旋量为公差域范围，需通过蒙特卡洛仿真进行大规模实验，再利用统计分析获得末端误差的分布区间。若仿真次数不够，无法获得功能要求方向变动的最大区间；如果仿真次数过多，增加了模型的计算量，且求解时间过长。若能直接推算出末端误差的最大分布区间，则不仅能减少计算时间，还能提高计算精度。

由式(1)可得x轴方向的误差：

(6)

(7)

在x轴方向上误差区间的右边界为：

(8)

式中，当τi(N,1)指数(-1)k和(-1)j的值大于0时，τi(N,1)取右边界，反之取左边界。所以，x轴方向上的最大误差为：

式(7)和式(8)指出了x轴方向末端误差的最大分布范围，可通过平动矢量和转动量的边界约束求解，无需再次使用蒙特卡洛仿真。同理可得y轴和z轴方向末端误差最大分布范围。则装配体的雅克比旋量最值模型可表示如下：

(9)

(10)

式中，

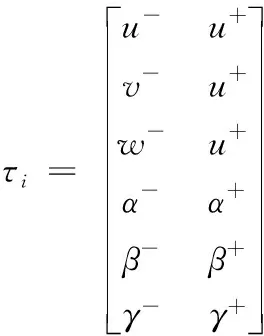
式中，N表示矩阵τi的第N行，N={1,2…6}；H表示雅克比矩阵的第H行，H={1,2…6}。

2.3 末端误差优化模型构建

公差优化是在给定的装配体内和相对经济的前提下，寻找最优的特征参数组合，以获得最小的末端误差。针对给定的装配体，寻找最优装配特征参数组合的优化模型如下：

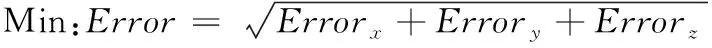
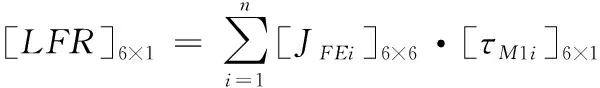
xi∈{CBDi,Di,Li,Ti}

(11)

式中，X表示各种装配特征参数的组合；xi表示第i个装配特征参数等级，它可能是CBDi、Di、Li、Ti，CBD代表孔和轴基本偏差代号；D和L是形位公差主要参数；T表示公差等级；Errorx、Errory、Errorz分别代表装配体x、y、z轴方向累积的末端误差；error是装配体的末端误差。

3 改进粒子群算法

粒子群优化算法(PSO)是一种群智能优化算法[10]，源于对鸟群捕食行为的研究，其基本思想是：通过群体中个体之间的协作和信息共享来寻找最优解[11]。粒子群算法本质上是一种连续优化算法，但通过一定转换，也已成功用于求解组合优化问题。针对装配公差优化问题，提出一种改进的粒子群算法(GRLPSO)，用于求解最优的装配特征参数组合。

3.1 编码和解码设计

在装配公差优化模型(11)中，优化对象为基本偏差代号、形位公差主参数和公差等级等离散变量。因此，将不同装配特征参数划分为不同的等级，各参数的每一等级对应不同的参数值。

以轴1圆柱度为例进行简单编码。通过分析式(5)，可以发现圆柱度公差的旋量参数取值区间受TU、TL、Tcyl和l四个常量的影响，鉴于加工难度和成本，通过变换配合类别来改变TU的取值，从而改变圆柱度公差的旋量参数取值区间，是比较合理的手段。若与轴1配合的孔为标准件，其公差等级为IT6，通过查询基孔制优先常用配合表[12]，可得到轴基本偏差代号为f～t。将其划分为不同的等级，得到如表1所示的简单编码，即可表示各特征参数的对应范围。

表1 装配特征等级

故而，各装配参数的编码设计可如图2所示。将各装配特征参数FE1～FE6依照序号顺次排列，得到编码{2,3,2,1,5,4}，如其中特征FE1表示轴1的圆柱度。第一个参数的特征等级为2，查询表1，可得到其基本偏差代号为g。同理，可得到其余装配特征参数的参数值。

图2 案例的一个编码

在上述编码基础上，利用式(5)，获得小位移旋量参数；同理，建立其余特征的小位移旋量模型。再利用雅克比旋量最值模型如式(9)和式(10)所示，计算出末端误差的最大分布区间；最后，利用式(11)，求得装配体末端的误差值。

3.2 PSO进化算子

PSO算法的粒子速度和位置迭代更新表达为：

(12)

Xk+1=Xk+Vk+1

(13)

式中，Gbest为整个种群中令末端误差最小的最优装配特征参数等级组合；Pbest为在局部范围内令末端误差最小的最优装配特征参数等级组合；惯性权重ω采用自适应惯性权重[13]，其最大值和最小值分别为{0.9、0.4}。

通过式(12)和式(13)，粒子位置Xk+1变成了实数。为此，采用Sigmoid方程进行离散化处理，使得粒子位置能表征装配特征参数等级。

3.3 算法其它改进

为防止算法陷入局部最优，在PSO基础上引入遗传算法的交叉操作来实现不同粒子之间的信息共享，变异操作实现粒子内部信息共享。同时，各个装配特征参数之间相互关联，可能需要变化多个参数才能获得更小的末端误差。为提升算法性能，引入反向学习策略，让部分编码片段的元素值发生变化，剩余位置保持不变，位置发生变化的数量通过下面公式进行计算。

式中，N为需要反向学习的位置个数；n为装配特征的总个数，k={1,2,3,…,n}。在粒子上随机产生N个位置，并标记为1，位置标记为1的元素值进行反向学习。

Bi=1+Di-Bi

表2 蒙特卡洛仿真取值与末端误差

式中，Bi为当前位置第i个装配特征的参数等级，i={1,2,3,…,N}；Di为第i个装配特征的最大等级。

为了让算法在迭代次数增加后，更容易跳出局部最优，需要引入惩罚函数机制。该机制能够让交叉概率Rc和变异概率Rm随着优化进程的进行，逐步达到最大值。惩罚函数可以表示如下:

Rc=Rc,min+(Rc,max-Rc,min)·progpen

Rm=Rm,min+(Rm,max-Rm,min)·progpen

式中，Rc,min和Rm,min分别是Rc和Rm的最小值；Rc,max和Rm,max分别是Rc和Rm的最大值。

3.4 算法流程

根据前文中GRLPSO方法的模型构建和求解过程，GRLPSO的伪代码如下：

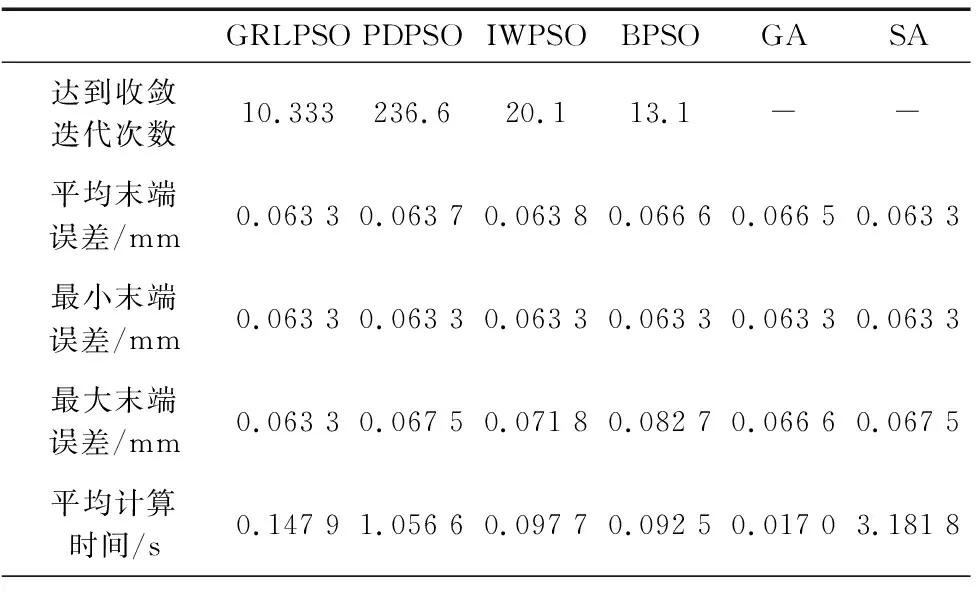
过程:GRLPSO方法Input:种群规模NP,装配特征参数,迭代次数G,特征维度DBegin:x←randi(NP,D);v←rand(NP,D);Pbesti←x;Gbest←min(fit_Pbest);For k=1 to G doωi=F(ωi-1) //权重更新Ric=F(Ri-1c) //交叉概率更新Rim=F(Ri-1m) //变异概率更新For i=1 to NP dox'i←x'i-1+vi;xi=S(x'i) //基于Sigmoid的离散If ∃x∉xlim then //超出左右边界限制x←xlim;End Ifx'i←交叉(xi,Ric); //交叉操作x'i←变异(xi,Rim); //变异操作x'i←反向学习(xi); //反向学习策略If fit_xi

4 案例分析

4.1 最值模型有效性

图3 蒙特卡洛参数校验图

从表2和图3中可以发现：随着N的增加，计算时间变长，各个方向的误差不断变大，但方差不断减小。当N较小时，虽然模型求解时间短，但是误差值却远小于N较大时的误差值，且数据的稳定性也不够，无法获得装配体末端误差的真实值；当N=4时，末端误差为0.36 mm，更接近装配体末端误差的真实值，方差也更趋近于0，但是，单次求解的时间需要57 s左右。而最值模型数据稳定，求解时间短，单次求解时间仅需0.034 s。图4为N=4时其中一次求解的末端误差分布情况，从中可以发现：通过最值模型求解的误差值大于蒙特卡洛仿真获得的误差值，说明雅克比旋量最值模型求解的末端误差更接近真实值，模型具有效性。

(a) x轴误差概率分布图 (b) y轴误差概率分布图

4.2 算法性能分析

结合遗传操作和反向学习策略对PSO算法进行改进，与标准的PSO算法、常用的改进方法(改进惯性权重取值IWPSO、改进种群多样性PDPSO)、遗传算法和模拟退火算法进行比较。30次求解结果如表3所示。

表3 算法性能比较

续表

从实验结果可以发现：GA算法的求解时间虽然较短，但是最优解较差，只有3.33%的概率能找到最优解；SA算法获得最优解的概率能达到96%左右，但是相对其它算法求解时间较长，约为4 s；标准PSO算法获得最优解的概率只有26.67%，其它两种改进算法性能有所提升，但也不能保证100%获得最优解。GRLPSO算法除了求解时间在1 s以内之外，还能够保证每次都找到最优解。这是因为设计的交叉和变异算子能够增加粒子间的信息交流，反向学习策略符合装配特征参数之间相互关联的实际情况。综上可知本文提出的GRLPSO算法在求解此问题时，能够优于标准的PSO算法、其它改进的PSO算法、遗传算法和模拟退火算法，具有良好的性能。