基于主元分析算法的电费抄核收数据异常诊断方法

施文

（国网陕西省电力公司，陕西西安 710048）

1 引言

电费抄核收数据异常诊断是一项十分重要的工程，随着科学技术的迅猛发展，电力企业中的抄核收工作人员不仅要提升自身的专业水平，同时还要充分利用现代科学技术提升自身素养[1]。电力企业要充分认识到电费抄核收数据异常诊断在整个流程中的重要性，并且要投入大量的精力采取有效的措施，促使电费抄核收数据异常诊断结果更加准确。最近几年，相关专家也加强了该方面内容的研究，例如裴茂林等人]将智能电表设定为用户和电网的信息枢纽[2]，通过电网为用户提供用电习惯以及负荷特征等相关信息进行数据异常诊断。杨茂等人分析风电功率特征[3]，通过Copula函数获取概率功率曲线，同时结合异常数据的时序特征建立数据异常诊断模型。以上两种方法虽然现阶段取得了较为满意的研究成果，但是由于未能进行数据去噪，导致电费抄核收数据异常诊断准确性降低，诊断延时上升。为此，提出一种基于主元分析算法的电费抄核收数据异常诊断方法。仿真实验结果表明，所提方法不仅可以全面增强电费抄核收数据异常诊断准确性，同时还能够降低诊断延时。

2 电费抄核收数据异常诊断方法

2.1 电费抄核收数据去噪预处理

在采集电费抄核收数据的过程中，许多数据存在尖峰或者突变现象，并且噪声也不是平衡的白噪声，对于这种信号的处理，采样传统的傅里叶变换是无法实现去噪的。由于傅里叶分析是完全在频域中进行信号分析，无法获取信号在任意时间段的变化情况，促使信号在时间轴上的随机一个突变都会影响整个信号的图谱[4-5]。而小波分析不仅能够同时在时域和频域中对信号进行分析，还能够准确区分信号中的突变部分以及噪声，有效实现噪声消除。

对于函数φ(t)∈L2R，如果进行傅里叶函数，则需要满足以下的可容性条件：

上式中，φ(t)代表基本小波或者小波母函数，将小波母函数φ(t)进行伸缩或者平移；同时尺度因子为a；平移因子为b，令经过平移后的函数为φ(a,b)(t)，则有：

上式中，φ(a,b)(t)代表依赖于a、b的小波基函数[6]。

将任意L2R空间中的函数f(t)在小波基下展开，将展开的函数f(t)称为连续小波变换，具体的表达式为：

其中：

当实际采用小波方法进行去噪时，小波变换的尺度参数不需要进行连续取值，而是采用一种方式将连续小波及其变换进行离散化处理[7]。通常情况下，将尺度a 按照幂级数进行离散化处理，对位移b进行均匀离散取值，经过离散后可以表示为：

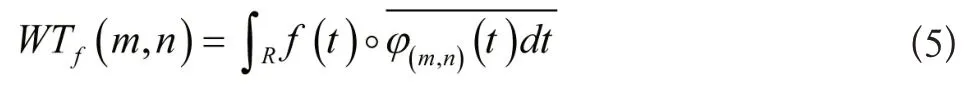
其中：

通过公式(6)能够得到第m个倍频的局部信息；f(t)的小波分解和重构可以根据Mallat 塔式算法进行计算。任意尺度的逼近信号均可以表示成下一程度的逼近信号和细节信号之和，即：

通过二进离散小波对信号进行三层分解，具体可以表示为：

在实际应用的过程中，有用信号可以表示为低频信号或者是部分较为平稳的信号，而噪声则可以表示为高频信号，所以在降噪的过程中需要进行以下处理：首先对初始信号进行小波分解；其次对小波分解的高频系数利用门限值等形式进行量化处理；最后对信号进行重构，即可达到降噪的目的。设定噪声的一维信号为：

上式中，f(i)代表真实信号；e(i)代表噪声；s(i)代表含有噪声的信号。通常情况下，一维的降噪过程可以划分为以下的步骤为：

(1)信号的小波分解：

选取小波分解，同时确定分解的层次N；然后对各个层次的高频系数进行量化处理。

(2)高频系数的阈值量化处理：

选取合适的阈值对1～N从层的高频系数进行量化处理。

(3)小波重构：

通过小波分解的第N层系数和经过量化处理后的第1～N层的高频系数，进而实现小波的重构。

在上述步骤中，关键是阈值的选择和量化的处理，这会直接关系到信号的质量，阈值选择方法主要包含以下几种形式，分别为：通过stein的无偏似然估计、启发式等。

在数据曲线中，非反射点的阈值是其损耗的经验值，它主要是由不同的连接技术以及工艺决定的。

针对信号f 进行阈值处理时，主要包含软硬阈值两种方法。其中硬阈值是将信号变换的绝对值和阈值进行对比，小于或者等于阈值的点变为零，而大于阈值的点则保持不变[8]。通过研究发现，软阈值的去噪效果明显优于硬阈值。

2.2 基于主元分析算法的电费抄核收数据异常诊断模型建立

主元分析在数据预处理方面具有十分明显的优势，尤其是在处理复杂数据的应用方面。它主要是将其和其它多元技术进行结合。首先针对子系统中的随机信号进行压缩处理，构建一个统一的大系统降维统计模型—PCA模型；然后提取系统中PCA 模型输出的统计特征参数，通过分析结果采用人工智能技术进一步判定故障的具体位置以及性质，并且对其进行一体化处理，将全部变量有效保留在PCA模型中。

主元分析主要是通过初始变量间的相关性，采用初始变量的少数线性组合对原始变量信息进行解释，进而有效实现数据降维。通常情况下，通过主元分析方法获取的主元变量和初始变量之间存在以下的关系，即：

(1)通过不同主元组成初始变量的线性组合；

(2)初始变量数量明显高于主元数量；

(3)主元有效保留了初始变量的大部分信息；

(4)不同主元之间不是相互关联的。

对于2.1小节经过小波变换的数据进行主元分析，采用主元分析算法是在确保电费抄核收数据信息丢失最少的情况下，对高维变量空间中的数据尽可能采用综合变量表示，主元个数是主元分析模型中十分重要的参数；当所使用的主元数量太少时，会导致变量中的信息丢失，且模型的误差增加；当采用较多的主元时，又会将数据中的测量噪声过多地引入过来，增强分析的计算量和诊断的复杂性，所以主元个数的确定十分重要。

设定正常状态下采集到的电费抄核收观测数据为X，其中共计含有m个观测变量以及n个观测值，采用m×n的数据矩阵代表这些数据，即：

其中矩阵X能够分解为以下的形式：

设定X的方差为：∑=COV(X)，其中∑的特征值可以表示为λ1，λ2，…，λm，同时λ1≥λ2≥…≥λm，结合矩阵的分解定理能够获取：

通过相关系数矩阵对电费抄核收数据主成分进行求解，即：

明确数据贡献率的主元数量，主要通过方差累积贡献率进行主元数量确定，具体的计算式为：

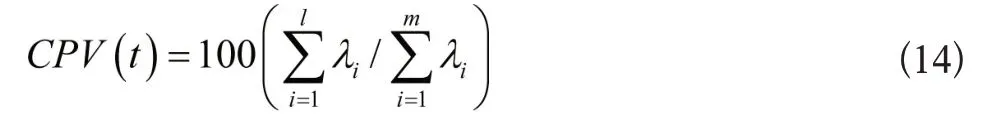
当前l 个主元的累积贡献率百分比超过一个阈值，利用这个阈值结合实际情况确定主元量。

在上述分析的基础上，将采集到的电费抄核收数据设定为训练样本，通过公式(15)选取合适的滞后时间，为了能够更好地提取动态变量间的相互关系，即：

通过公式(16)进行数据训练，获取对应的数据阵：

通过公式(14)对公式(16)进行标准化处理，获取均值以及标准方差。

在上述分析的基础上，计算SPE统计量和T2统计量在置信度α的控制限，即：

采集故障数据将其设定为测试数据，同时组建测试数据对应的数据向量。同时将数据向量分别分解到不同的主元子空间和残差子空间中，获取 和 。同时，采用公式(19)和公式(20)计算T2的统计量和SPE统计量，即：

绘制T2和SPE多变量统计控制图，同时实时监控系统的运行状态。

同时利用主元分析表达式建立数据异常诊断模型，通过模型实现电费抄核收数据异常诊断，即：

综上所述，完成了电费抄核收数据异常诊断。

3 仿真实验分析

为了验证所提基于主元分析算法的电费抄核收数据异常诊断方法的综合有效性，在Win7 系统，CPU i55600U@2.6GHz，内存16GB3200MHz下进行仿真实验测试。

由于所提方法在研究初期使用小波变换对采集到的电费抄核收数据进行去噪处理，利用表1给出所提方法的去噪效果。

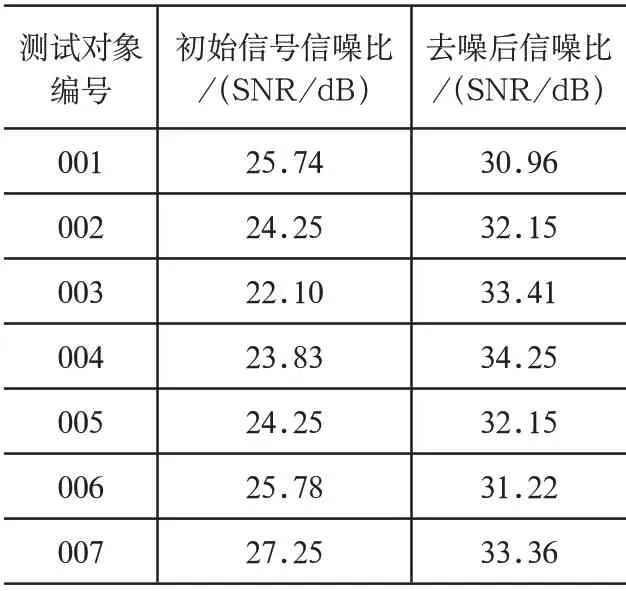
表1 所提方法的去噪效果

分析表1中的实验数据可知，所提方法能够有效提升数据的信噪比，同时有效抑制数据的震荡现象，对异常数据处理效果明显。

为了验证电费抄核收数据异常诊断结果的准确性，实验选取平均绝对误差和平均误差设定为测试指标，其中两项指标的取值越低，则说明电费抄核收数据异常诊断结果准确性越高，反之则说明电费抄核收数据异常诊断结果准确性越低。实验选取两种方法作为对比方法，利用表2～表4给出三种方法的电费抄核收数据异常诊断结果准确性对比结果：

分析表2～表4中的实验数据可知，所提方法有效降低了电费抄核收数据异常诊断结果的平均绝对误差和平均误差，促使所提方法的电费抄核收数据异常诊断结果更加准确。这主要依赖于所提方法的研究初期，采用小波变换对采集到的电费抄核收数据进行去噪处理，有效滤除数据中的噪声，全面提升数据异常诊断结果的准确性，且所提方法明显优于另外两种方法。

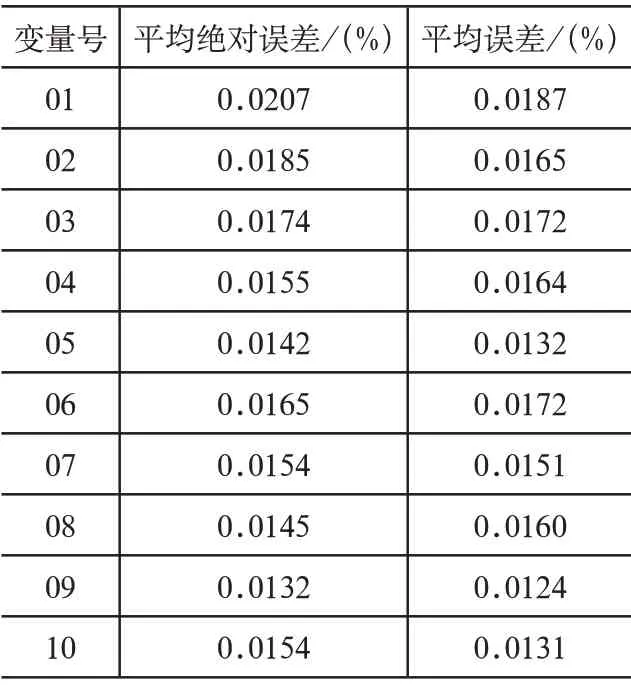
表2 所提方法的电费抄核收数据异常诊断结果准确性

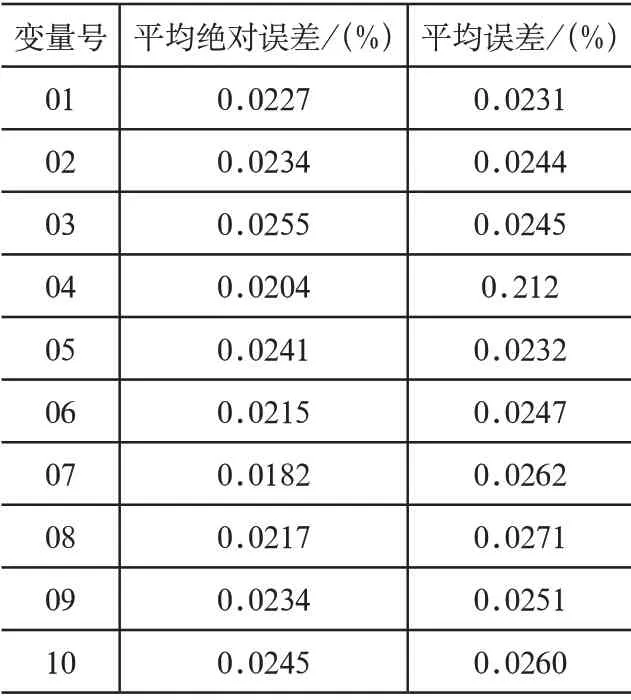
表3 文献[2]方法的电费抄核收数据异常诊断结果准确性

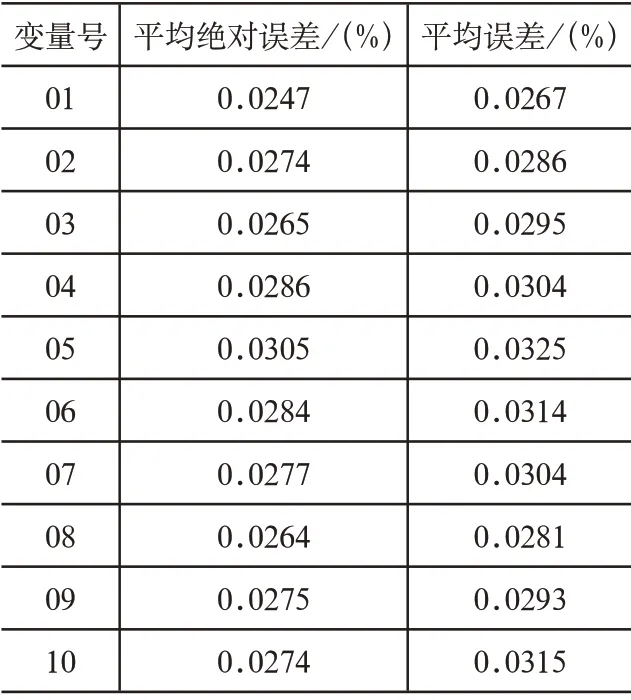
表4 文献[3]方法的电费抄核收数据异常诊断结果准确性

在进行电费抄核收数据异常诊断的过程中，由于受到各种各样外界因素的干扰，导致各个方法均存在诊断延时，以下实验测试将电费抄核收数据异常诊断延时设定为测试指标，分别选取文献[2]方法和文献[3]方法作为对比方法，利用图1给出具体的实验对比结果。

分析图1中的实验数据可知，各个方法的电费抄核收数据异常诊断延时会随着测试样本数量的增加而增加，但是和另外两种方法相比，所提方法的电费抄核收数据异常诊断延时明显更低一些，这是因为所提方法采样小波变换对采集到的电费抄核收数据进行去噪处理，有效滤除无利用价值的数据，减少电费抄核收数据异常诊断延时。

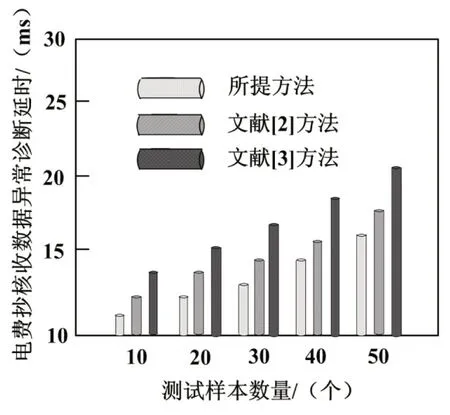
图1 不同方法的电费抄核收数据异常诊断延时对比结果

4 结束语

为了有效提升传统方法的电费抄核收数据异常诊断准确性，降低电费抄核收数据异常诊断延时，结合主元分析算法，提出了一种基于主元分析算法的电费抄核收数据异常诊断方法。通过具体的仿真实验测试，全面验证了所提方法的有效性和优越性。