移动边缘计算场景下基于免疫优化的任务卸载

朱思峰，孙恩林，柴争义

(1.天津城建大学 计算机与信息工程学院，天津 300384；2.天津工业大学 计算机科学与技术学院，天津 300387)

5G技术提出了三大应用场景[1]：增强型移动带宽(enhance Mobile Broad Band，eMBB)、海量接入(massive Machine Type of Communication，mMTC)、超高可靠和低延迟通信(ultra Reliable & Low Latency Communication，uRLLC)。随着低时延低能耗移动终端应用需求的大量涌现，满足低时延低能耗的移动计算模式成为了热点研究领域[2-3]。边缘计算通过把云服务中心的计算资源和存储移到移动终端的附件(即移动网络的边缘)，可减少云服务的通信时延，支持低时延应用服务，满足低延迟应用场景需求。移动边缘计算(Mobile Edge Computing，MEC)，即将云计算的服务器从核心网络下沉到靠近移动终端的网络边缘，已经成为一种有效的计算模式[4]。与传统云计算相比，边缘计算具有明显的优势：① 大量数据在MEC服务器进行处理，不需要将全部数据传输到中心服务器上进行存储，一方面降低了云计算服务中心的计算压力和存储压力；另一方面缓解了网络的带宽压力。② 数据处理在移动边缘计算服务器上执行，减少了数据上传到计算中心处理的高时延，从而提高系统的响应能力。③ 用户产生的隐私数据不需要上传到云数据中心，使得用户的隐私得到保障。④ 用户的大部分数据在边缘执行，使得计算中心的能耗大大降低。

目前，移动边缘计算场景下的卸载决策问题引起了国内外学者广泛关注：文献[5]把执行时延和任务成功率作为性能指标，提出了一种卸载动态优化方案；文献[6]研究了基于延时机制的多目标工作流调度算法，该算法使用遗传算法作为优化方法，结合了工作流之间的依赖关系，在编码的时候充分考虑了工作流中的任务执行位置和执行顺序，极大地降低了移动设备的能耗，缩短了任务执行的时延；文献[7]通过研究二进制卸载模型，考虑移动终端的计算模式选择、系统传输时延分配的联合优化问题，给出了一种最大化所有移动终端计算速度的优化方案；文献[8]研究了各个任务之间的依赖关系，提出了一种结合工作流调度的卸载策略，并设计了基于遗传算法的卸载策略；文献[9]将卸载任务构建成图结构，使用快速启发式算法寻找最优解决方案；文献[10]研究物联网环境中边缘计算问题，给出了一种基于遗传算法的任务卸载方案来提升物联网设备的通信效率；文献[11]提出一种缓存辅助边缘计算的卸载决策制定与资源优化方案，以进一步降低移动边缘计算系统中移动终端的能量消耗；文献[12]给出了一种移动边缘环境下能够联合优化多用户时延与移动边缘计算服务器资源分配平衡度的计算卸载方法；文献[13]研究了物联网移动边缘计算场景下基于时延约束感知的任务卸载策略。

上述文献所提方案从系统响应时延或移动终端能耗等方面进行考虑，给出了相应的任务卸载策略。不同于上述文献，笔者对系统响应时延和移动终端能耗进行综合考虑，给出了一种最小化系统响应时延和移动终端能耗的任务卸载方案。主要贡献是：(1)提出一种基于任务切分的边缘计算卸载优化模型；(2)给出了一种基于免疫优化方法的任务卸载解决方案。

1 移动边缘计算场景下任务卸载的系统模型

在移动边缘计算场景下，为了把云计算服务器从核心网络下沉到靠近移动终端的网络边缘，在移动基站附近部署移动边缘计算服务器。另外，为了缩短基站与移动边缘计算服务器之间的通信时延，移动基站与移动边缘计算服务器之间通过光纤相连接。移动终端处于基站的覆盖范围内，并通过无线与基站相连。移动终端把任务发送给基站，再由基站通过光纤传输到移动边缘计算服务器。笔者建立的系统模型如图1所示。在该系统模型中，假设某基站覆盖范围内有一台需要任务卸载的移动终端，基站通过光纤连接有一台移动边缘计算服务器。

笔者做的一些基本假设：

(1) 只考虑一个执行任务，并且执行任务是可切分。

(2) 每个任务均可以切分为多个子任务(进程)。每个子任务之间的依赖关系只有依赖于前一个子任务，或不依赖于前一个子任务。

(3)子任务上传到移动边缘计算服务器可以并行执行。

(4) 任务上传期间或者计算结果下载期间，通道的信号质量是稳定的。

(5) 移动终端执行计算任务和传输数据时的能耗是远远高于待机时的能耗。

(6) 移动终端和移动边缘计算服务器在执行任务时具有稳定的计算能力，并且MEC服务器的计算能力远远高于移动终端的计算能力。

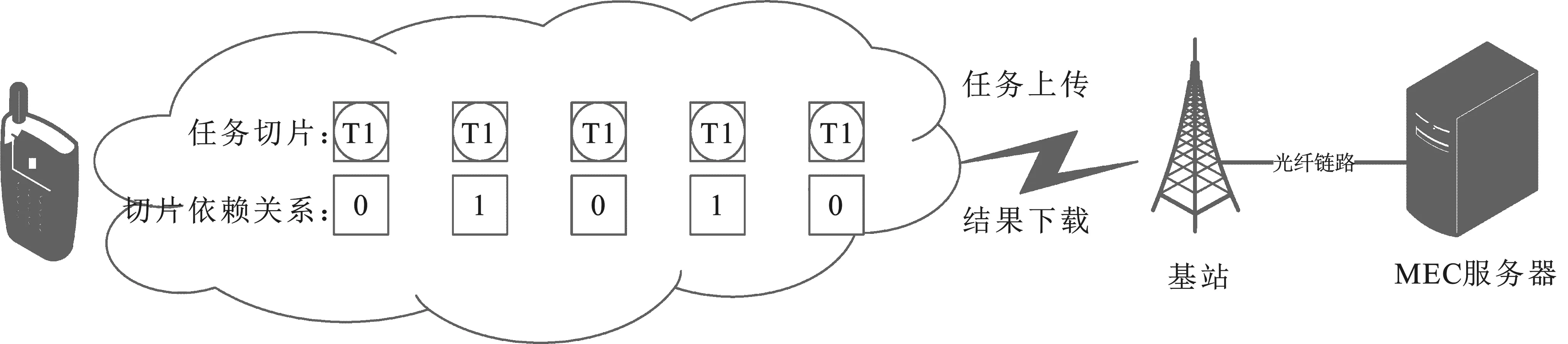
图1 系统模型

1.1 任务切分模型

假设移动终端上的任务T可切分成多个子任务，即任务T可以被划分为N个子任务的切片T={t1，t2，…，tN}。任务T可分为4部分，即T={Din，W，Z，Dout}。其中，Din表示将任务部署到MEC服务器时所需上传的数据量；W表示该任务的计算量；Z表示执行该任务需要的计算资源；Dout表示任务在MEC服务器上计算完成后，将计算结果下载到移动终端的数据量。

1.2 时延模型

假设移动终端的计算能力是恒定的，即移动终端的的计算能力为一个固定的值clocal；假设第i个计算子任务在本地执行，该子任务的计算时延为

(1)

假设移动边缘计算服务器的计算资源为ZMEC，计算能力在进行计算处理时是稳定的，记为CMEC；移动终端上传的传输速率是固定值为rup，移动移动终端下载数据任务的传输速率为rdown。若将第i个子任务上传到移动边缘计算服务器上进行计算，则第i个子任务的执行时延为

(2)

将第i个子任务卸载到边缘服务器执行时，除了考虑MEC服务器完成计算工作量产生的时延外，还需要考虑其前后两个子任务的卸载情况及其产生的相关时延。式(2)中对应了其前后两个子任务的卸载情况的4种组合。xi-1=0，xi=1，xi=0：第i-1个子任务和第i+1个子任务都没有卸载，此时要考虑了当前子任务的数据上传时延和计算结果下载时延；xi-1=1，xi=1，xi+1=0：第i-1 个子任务进行了卸载但第i+1个子任务没有卸载，此时要考虑当前子任务的计算结果的下载时延；xi-1=0，xi=1，xi+1=1：第i-1 个子任务没有卸载但第i+1个子任务进行了卸载，此时要考虑当前子任务的数据上传时延；xi-1=1，xi=1，xi+1=1：第i-1 个子任务和第i+1个子任务都执行了卸载，此时不需要考虑当前子任务的数据上传时延和计算结果下载时延。

每个子任务要么在本地执行，要么卸载到移动边缘计算服务器上执行。设决策变量xi表示第i个子任务卸载情况，xi=1表示第i个子任务卸载到移动边缘计算上执行，xi=0表示第i个子任务在本地执行，则执行任务T的总时延为

(3)

1.3 能量消耗模型

假定移动终端的能耗与执行任务的时延成正比，这个能耗系数与移动终端的组织结构有关，将其设为λ，则第i个子任务在本地执行的能耗模型为

(4)

当把第i个子任务卸载到移动边缘计算服务器上执行时，只需考虑数据上传过程和结果数据下载过程移动终端的能耗模型，如下所示：

(5)

其中，λ2是移动移动终端上传数据时的能耗系数，λ3是移动终端下载数据时的能耗系数。

每个子任务要么在本地执行，要么卸载到移动边缘计算服务器上执行。设决策变量xi表示第i个子任务卸载情况，xi=1 表示第i个子任务卸载到移动边缘计算上执行，xi=0 表示第i个子任务在本地执行，则移动终端执行第i个子任务的能耗模型如下所示，

(6)

移动终端执行任务T的总能耗模型如下所示：

(7)

其中，ECi代表执行第i个子任务的能耗。

1.4 优化模型

移动边缘计算场景下，最小化时延和最小化移动终端设备的能耗是待优化的2个目标。对系统响应时延和移动终端能耗进行综合考虑，使用权重系数平衡计算时延和能耗之间的比重，通过加权处理后把2个目标转化为一个综合代价目标，建立了一个最小化综合代价的约束优化模型，

(8)

2 基于免疫优化的任务卸载方案

近年来，仿生类智能优化算法获得了很大进展。模拟生物免疫系统的免疫调节、免疫识别、克隆选择、免疫记忆等机制而研制的免疫算法(Immune Algorithm，IA)在单目标优化、多目标优化、动态优化等方面性能表现优异，在资源调度、频谱资源优化、图像分类与识别等多个领域得到了广泛应用[14-18]。对于优化问题，纯数学方法的优点是理论上能找到问题的最优解。但当问题规模很大时，求解变得非常困难；另外，纯数学方法难以实现并行处理。相比于传统纯数学算法[19-20]，免疫算法具有结构简单高效和能够并行处理等优点。在工程上，侧重考虑方案的有效性，即在满足性能要求的前提下，找到较优的可行解决方案就可以了。对于大规模问题，纯数学方法难以胜任，而IA可以在满足性能要求的前提下找到较优的可行解决方案。对于实时性要求高的场景(在线处理)，IA方法比纯数学方法具有优势。基于此，文中采用IA方法来求解任务卸载问题。

2.1 抗体编码

将移动终端中的一个计算任务切分为多个子任务，子任务之间的依赖关系：每个子任务只依赖于前一个子任务，移动终端在同一时刻只能有一个子任务进行处理；当子任务传输到移动边缘计算服务器时，多个子任务可以并行执行。下面假设为一个任务可以切分为5个子任务，只有切片间依赖关系不同，执行位置相同，用来阐述依赖关系对执行时延的影响，如图2所示。

图2 子任务之间的依赖关系

图3 子任务的执行时延

子任务之间的依赖关系对任务执行时延的影响如图3所示。假设子任务T2在移动边缘计算服务器上执行，子任务T1、T3、T4和T5在本地执行；假设每个子任务执行的时延相同，每个操作都占用一个时延片单位，任务的执行和上传以及下载都占用一个时延片单位。当子任务T1和T2之间存在依赖关系时，只有执行完子任务T1，才能上传T2；反之，当子任务T1和T2之间不存在依赖关系时，可以在执行子任务T1时，将T2上传到MEC服务器上进行处理。任务T1比任务T2执行时延多一个时延片。

免疫优化算法求解问题时，把待求解的问题抽象为抗原，把问题的候选解抽象为抗体，通过在编码空间中进行启发式搜索来寻找最优抗体，解码最优抗体输出问题的最优解。文中对子任务执行的位置采用二进制编码方式，使用抗体X={x1，x2，…，xi，…，xN}表示子任务的调度结果的位置，其中，xi表示第i个子任务是否卸载到移动边缘计算服务器上进行执行，当xi=0时，表示该子任务在移动终端上执行；当xi=1时，表示移动终端需要将子任务卸载到移动边缘计算服务器上执行。

2.2 初始化

初始化模型的参数，如边缘设备和移动终端的计算能力、计算功率和传输速率等；初始化任务相关的矩阵，如各个子任务的计算量的大小、任务计算所需要上传的数据量、各个子任务之间的依赖关系和子任务执行位置的矩阵；初始化免疫算法的一些基本参数，如种群规模、变异概率、激励度系数、相似度阈值等；随机产生若干个抗体，对抗体种群进行初始化。

2.3 抗体亲和度评价函数

在免疫算法中，亲和度表征抗体与抗原的结合强度，与遗传算法中的适应度相对应。亲和度算子通常是表示为函数的形式，如f(X)，在文中采用的亲和度评价函数为

(9)

其中，X是抗体(问题的候选解)。

2.4 变异算子

对抗体采用二进制编码，对抗体进行变异操作的方法是对抗体的某一位进行随机取反，具体操作如图4所示。使用变异算子对得到的抗体方案进行变异操作，以增加抗体种群的多样性，实现局部范围内搜索。

图4 子任务计算位置变异操作

2.5 抗体浓度评价算子

抗体浓度的大小可以表示抗体种群多样性的好坏。当某种抗体浓度过高时，就说明抗体种群中的抗体趋于过度集中，可能会出现局部最优化，降低全局搜索能力。因此需要对浓度过高的抗体进行抑制，保证抗体种群的多样性。抗体浓度计算公式为

(10)

其中，den(Xi)为种群的抗体浓度；N为种群中的抗体个数；S(Xi，Xj)代表两个抗体之间的相似度，其表达式为

(11)

其中，δ表示相似度阈值，aff(Xi，Xj)是抗体之间的亲和度函数。采用海明距离作为抗体间亲和度的计算函数，

(12)

(13)

其中，xi，k和xj，k分别表示为抗体i和抗体j的第k个决策变量；N表示任务可切分的子任务的总数。

2.6 激励度算子

对抗体的质量进行评价需要综合考虑抗体的亲和度和抗体浓度两个方面。通过对激励度的排序，选出前N/2个抗体进行变异和克隆抑制等免疫操作。在一般情况下，亲和度较大而浓度较低的抗体应该具有较高的激励度。激励度函数计算公式为

sim(Xi)=αaff(Xi)-βd(Xi)，

(14)

其中，sim(Xi)代表方案Xi的激励度；α，β分别代表抗体亲和度和抗体浓度的权重系数。在文中令α=2，β=1。

2.7 求解任务卸载的免疫算法流程

(1) 初始化模型的参数，如边缘服务器的计算资源和计算能力、移动终端的计算能力、计算功率和传输速率等；

(2) 初始化任务相关的矩阵，如各个子任务的计算量、需要上传的数据量、下载的数据量、需要的计算资源、各个子任务之间的依赖关系和子任务执行位置的矩阵；

(3) 初始化免疫算法的一些基本参数，如种群规模、变异概率、激励度系数、相似度阈值等；

(4) 对抗体种群进行初始化；

(5) 进行抗体浓度、抗体间亲和度和抗体激励度的计算；

(6) 根据抗体激励度对抗体进行按升序排列；

(7) 选取前N/2个抗体进行变异和克隆抑制等免疫操作，生成新的种群；

(8) 计算新生成种群的激励度，将新的种群与免疫种群进行合并，更新种群；

(9) 判断是否满足循环结束条件，如果是，则结束循环，对抗体种群中的最优抗体进行解码，输出最优的任务卸载方案；否则返回步骤(5)。

3 仿真实验及分析

采用Matlab软件进行系统仿真，其中，每个子任务的计算量在[1，100]区间上随机生成；每个子任务上传和下载数据量在[1，25]区间上随机生成；移动终端的计算能力、计算功率、数据上行功率与速率、数据下行功率与速率以及移动边缘计算服务器计算能力等，如表1所示。

表1 移动终端和MEC服务器性能参数

把基于免疫算法(IA)的方案，与文献中基于遗传算法(Genetic Algorithm，GA)的方案和基于LOCAL Execution(LOCALE)的方案进行对比实验。基于GA的方案对子任务的执行位置使用遗传算法进行计算处理，不考虑子任务之间依赖关系。基于LOCALE的方案将所有任务都放在移动终端上进行处理计算。免疫算法的种群规模N=50；GA算法和LOCALE算法设置的初始候选解的个数均为50个；随机工作流的子任务数为50。

把任务时延和终端能耗的加权和作为执行任务的综合代价，在相同的条件下，比较IA方案、GA方案和LOCALE方案的综合代价。下面从子任务数量变化、子任务执行时所需要的上传和下载的数据量的变化、子任务计算量的变化、权重系数变化等方面进行对比实验。

3.1 子任务数量变化对综合代价的影响

观察图5可知：随着子任务数量的不断增加，综合代价明显增加。这是因为计算量的增加，必然导致执行任务会消耗更多的时延和能量。通过对比不同卸载方案可以发现，当任务数量较小时，3种方案的综合代价相差不大，但随着任务量的增加，笔者提出方案的综合代价增长缓慢，优于GA方案和LOCALE方案。

3.2 传输数据量(Din+Dout)变化对综合代价的影响

考察综合代价随数据传输量(数据上传)的变化情况，将数据传输量取值区间限定在5个区间，3种方案的综合代价(ω=0.5，时延和能耗同等重要)随数据传输量增加的变化情况如图6所示。

从图6可以看出：随着传输数据量的增加，3种方案的综合代价都在增加；LOCALE方案是本地执行，系统时延主要与计算量有关，与传输数据量关联度很小，所以系统时延和终端能耗加权和生成的综合代价与传输数据量关联度不大；在相同的数据量区间，IA方案比GA方案具有更小的综合代价，但是相差较小。

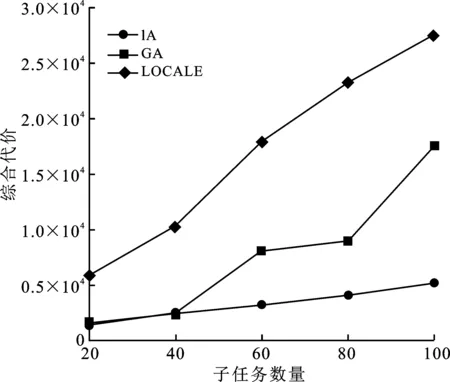
图5 综合代价随子任务数量增加变化情况

图6 综合代价随传输数据量增加的变化情况

3.3 计算量变化对综合代价的影响

考察综合代价随计算量的变化情况，将计算量取值区间限定在5个区间，3种方案的综合代价(ω=0.5，时延和能耗同等重要)随计算量增加的变化情况如图7所示。

从图7可以看出：LOCALE方案是本地执行，随着计算量的增加，其综合代价增幅最大，综合代价与计算量呈正相关；GA方案和IA方案增幅缓慢，明显优于LOCALE方案；在相同的计算量区间，IA方案略优于GA方案，但是相差较小。

3.4 权重系数(ω)对综合代价的影响

考察综合代价随权重系数的变化情况，将权重系数(ω)分别取0.3、0.4、0.6、0.7，3种方案的综合代价随权重系数的变化情况如图8所示。

图8比较了4种不同权重状态下的综合代价平均值，可以看出权重对每种方案都有所影响。在每种权重下，笔者所提方案均不输于其他的方案。但是随着权重的增加，笔者所提方案在保持优势的情况下，具有最小的波动，受权重的影响比较小。

图7 综合代价随计算量增加的变化情况

图8 权重系数对综合代价的影响

3.5 单独考察系统时延和终端能耗

为了进一步比较3种方案，单独考察系统时延和终端能耗随子任务数量变化情况。图9展示了仅考察系统时延(ω=1)时，3种方案的时延随子任务数量的变化情况。

从图9可以看出：LOCALE方案在本地执行，随着子任务的增多，系统时延增长很快；文中方案通过优化卸载策略，在系统时延性能上表现优于GA方案和LOCALE方案。

图10展示了仅考察终端能耗(ω=0)时，3种方案的能耗随子任务数量的变化情况。

从图10可以看出：LOCALE方案在本地执行，随着子任务的增多，终端能耗增长很快；文中方案在终端能耗性能上略逊色于GA方案，原因是文中方案侧重于把子任务卸载到MEC服务器，数据上传和下载产生了较多的能耗。

图9 子任务数量对系统时延的影响

图10 子任务数量对终端功率的影响

4 结束语

笔者研究了移动边缘计算场景下单个移动终端任务可切分的卸载问题，综合考虑系统时延和移动终端能耗，把移动终端的计算任务进行切分，设计了任务卸载优化模型，并用免疫优化算法求解该模型。仿真实验表明，与本地执行(不进行卸载)方案和基于遗传算法的卸载方案相比，笔者提出的基于免疫算法的卸载方案具有更好的性能，具有较好的应用价值。

下一步工作，将研究存在多个移动终端、多个边缘服务器、边缘计算场景下多约束(如：时延约束、移动终端能耗约束等)条件下的任务卸载问题。