余弦方波电压频率对电缆典型绝缘缺陷击穿时间的影响

2022-04-25魏力强苏金刚伊晓宇张姿姿郭小凡

绝缘材料 2022年4期

刘振，魏力强，张鹏，苏金刚，伊晓宇，张姿姿，郭小凡

（国网河北省电力有限公司电力科学研究院，河北石家庄 050021）

0 引言

交联聚乙烯（XLPE）电缆绝大多数的击穿事故与电缆的主绝缘状态关系密切[1]。耐压试验是考核电缆绝缘性能的基础试验，也是电缆投运前必须进行的一项交接试验，可以发现绝缘内部是否存在较大缺陷。当前电缆耐压试验主要包括交流耐压和0.1 Hz超低频耐压试验。由于电缆容量大，采用交流耐压试验的功率需求高，设备体积庞大，现场实施困难，所以功率需求低、设备体积小的0.1 Hz超低频耐压试验被广泛采用[2-5]。

超低频包括正弦波和余弦方波两种，其中余弦方波设备的功率需求低，极性转换波形接近50 Hz的工频电压，是一种新型的试验电压波形。当前余弦方波电压的研究主要集中在波形产生的方法[6-8]、击穿电压的等效性等方面[9-12]。不同于正弦波，余弦方波由于其波形的产生机制，可以较为方便地增加频率，而其功率需求的增加不明显。但受电力电子开关器件工作频率和充放电过程的影响，波形会随频率的增加出现一定程度的畸变。当前研究表明，电压频率的增加可以加快电树枝的生长速度，缩短击穿时间[13-14]。但对于余弦方波电压是否可以通过增加电压频率缩短击穿时间，进而提高耐压试验的效率问题尚不清楚。

针板电极缺陷和水树缺陷是电缆中两种代表性的缺陷，也是导致电缆击穿的主要原因。针板电极缺陷会在电缆内部形成极不均匀的电场，严重降低电缆的击穿电压[15-16]。当XLPE中有水分时，在较低场强下即可诱发水树[17-18]，水树在一定条件下会转化为电树[19]，进而导致电缆击穿。

本研究制备了针板电极缺陷和水树缺陷模型，分别利用0.1、0.5、1.0 Hz的余弦方波电压进行击穿试验，统计击穿时间的分布和击穿点的时刻，观测击穿通道的微观形貌，并讨论余弦方波电压频率对电缆典型绝缘缺陷击穿时间影响的作用机制。

1 典型绝缘缺陷的制作

1.1 针板电极缺陷模型

针板电极缺陷是绝缘缺陷的典型代表，会在电缆内部形成极不均匀的电场。但传统针板电极多数采用针电极直接插入XLPE试样的方式。由于XLPE具有一定的硬度，针电极插入的深度和角度都不易控制，尤其是针电极插入的深度对针电极位置电场分布影响很大，导致针电极与板电极间的距离也就是绝缘剩余厚度控制不理想，针尖位置的电场分布一致性差，试验结果的分散性也较大。

为此，本研究设计了一种针板电极模型，其整体结构如图1所示。其中电极均采用GB∕T 1408.1—2016所规定的等直径电极，采用直径为25 mm、边缘倒角为3 mm的黄铜材料制成。针电极为钨针电极，头部直径为1 mm，曲率半径为20 μm。XLPE压片试样，尺寸为100 mm×100 mm×2 mm。

图1 针板电极模型Fig.1 Needle plate electrode model

试验时，首先将XLPE压片试样用高压电极与低压电极压紧。然后在高压电极中置入旋进式的钨针电极，电极尾部为螺丝，螺距为1 mm。最后通过带有刻度的旋转盘控制钨针电极的插入深度，每旋转36°针电极深入0.1 mm。由于针尖较短，承受压力减小，其自身形变很小。旋进结构可以有效控制针电极插入深度，绝缘剩余厚度可控性高。通过控制针电极的插入深度，制备了绝缘剩余厚度为0.2 mm的电极模型。试验时，将电极模型整体置入油箱中，并充入25#变压器油，防止XLPE试样发生沿面闪络。

1.2 水树缺陷模型

水树缺陷基于厚度为1 mm的XLPE压片试样制备。试样尺寸为50 mm×50 mm×1 mm，取中心直径为20 mm的区域作为加速水树老化培养区域。为提高培养水树缺陷的成功率，试验中采用水刀电极法，将刀片沿垂直试样表面方向压入内部，如图2所示。在试样表面形成3个长度为3 mm的刀口，保留绝缘厚度为0.5 mm，将刀口位置培养出的水树作为试验中XLPE的缺陷。

图2 XLPE样本示意图Fig.2 XLPE sample schematic

本研究采用IEC/TS 61956:1999推荐的杯状试验槽对XLPE压片试样进行加速水树老化试验，并对杯状试验槽进行改进，试验槽的结构如图3所示。

图3 杯状试验槽结构Fig.3 Cup-shaped test groove structure

同时为防止氯化钠溶液由于水的表面张力无法进入刀口缺陷当中，先向杯状试验槽中加入适量的浓度为1 mol/L的氯化钠溶液，在23～25℃室温条件下，将试验槽放入真空干燥机中多次抽真空，再向试验槽内注满氯化钠溶液。

为提高效率，试验将10个试验槽并联，施加频率为10 kHz、有效值为1.5 kV的高频电压，以激励水树的快速生长。

典型水树缺陷的切片图像如图4所示。当前研究认为，水树的长度是影响击穿的主要因素，因此选择长度来判断水树生长和击穿的关系。本研究针对水树长度进行了定义，图4中D为刀口至切片另一侧距离，约为0.5 mm，D1为水树垂直方向最长点距离刀口的距离。

图4 典型水树缺陷切片图片Fig.4 Section image of typical water tree defects

水树生长具有一定的分散性，无法精确控制其长度占比。通过反复试验摸索，确定了水树长度占比和对应加压时间的大致对应关系。击穿试验中采用了加压时间为120 h的试样，其水树长度的占比约为90%。

1.3 水树生长长度和击穿通道形貌的观测

水树的生长长度和击穿通道的形貌采用切片机配合显微镜进行。切片机的作用是对试样进行纵向剖切，其精度为1 μm，显微镜的使用放大倍数为20倍。

对于水树长度的观测，首先沿垂直刀口方向切取厚度约为200 μm的薄片，浸泡在90℃的亚甲基蓝中染色4 h，待充分染色后，用无尘布擦拭，然后放在显微镜下观察水树枝的生长情况，并采用显微镜配套的软件对水树由刀口方向生长的长度进行测量。

对于击穿通道形貌的观测，分别对XLPE压片的击穿通道的表面和纵向剖切通道进行观察。

2 结果与分析

2.1 余弦方波电压频率对针板电极模型缺陷击穿时间的影响

试验施加电压为30.75 kV，该电压数值为10 kV电缆的2.5U0。由于击穿时间的分散性较大，采用两参数威布尔（Weibull）分布对击穿试验数据进行处理统计[20]。两参数Weibull分布密度函数表达式如式（1）所示。

对式（1）作对数变换可得式（2）。

式（2）中：t表示可测变量，即击穿时间；F(t)表示在击穿时间t时的失效概率；α表示尺度参数，指失效概率为63.2%时的击穿时间；β表示形状参数，理论上为式（2）的斜率，表示试验数据的分散性，β越大，击穿时间的变化范围越小。采用White方法计算α和β的数值。

余弦方波电压下，针板电极缺陷试样的击穿时间和击穿概率如图5所示，据此计算的α尺度参数和β形状参数如表1所示。从图5和表1可以看出，在0.1 Hz的余弦方波电压作用下，所测量10组试样中多达6组试样在3 h的加压时间内未击穿，试样的Weibull击穿时间为348.6 min。在0.5 Hz的余弦方波电压作用下，试样的Weibull击穿时间为32.5 min。在1.0 Hz的余弦方波电压的作用下，试样的Weibull击穿时间为21.7 min，缺陷试样的Weibull击穿时间随余弦方波电压频率的增加而显著缩短。同时形状参数β有所增大，说明击穿时间的分散性有所降低。对于0.1 Hz的余弦方波电压，最短Weibull击穿时间为27.5 min，最长的超过3 h未击穿。而对于1.0 Hz的余弦方波电压，最短Weibull击穿时间为9 min，最长Weibull击穿时间也仅为30.2 min，击穿分散性下降，也是击穿概率提高的表现，说明在该电压频率下，缺陷击穿的概率更高。

图5 不同频率的余弦方波电压下击穿时间的威布尔分布Fig.5 Weibull distribution of breakdown time under cosine square wave voltage with different frequency

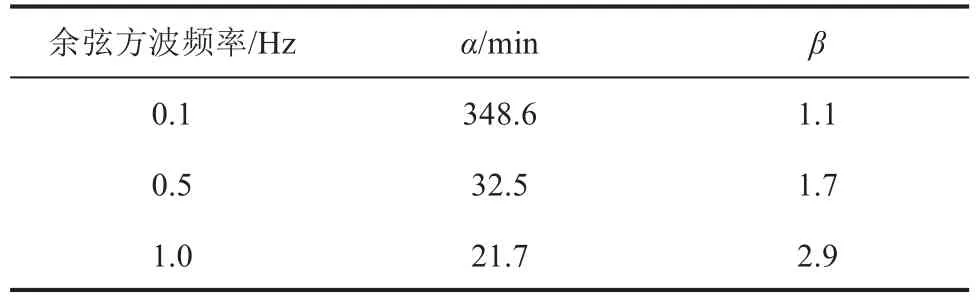
表1 不同频率余弦方波电压下击穿试验的尺度参数和形状参数Tab.1 Scale and shape parameters of breakdown test under cosine square wave voltage with different frequency

2.2 余弦方波电压频率对水树缺陷击穿时间的影响

试验施加电压为7.5 kV，其平均场强与10 kV电缆3U0下的平均场强一致。不同频率余弦方波电压下水树缺陷的击穿时间如表2所示。从表2可以看出，在0.1 Hz的余弦方波电压作用下，试样的击穿时间均不超过15 min，在0.5 Hz的余弦方波电压作用下，试样的击穿时间则均不超过5 min，在1.0 Hz的余弦方波电压的作用下，试样的击穿时间则均不超过2 min。水树缺陷的击穿时间随余弦方波电压频率的增加而显著缩短。

表2 不同频率余弦方波电压下水树缺陷的击穿时间Tab.2 Breakdown time of water tree defect under cosine square wave voltage with different frequency

2.3 击穿通道的形貌特征对比分析

不同频率的余弦方波电压下针板电极缺陷击穿通道的典型形貌如图6所示。从图6可以看出，尽管击穿通道的直径没有显著差异，但0.1 Hz的余弦方波电压下击穿通道较为清晰，说明击穿的气化过程较为充分，击穿瞬间注入的能量较为充分。而在0.5 Hz和1.0 Hz的余弦方波电压下击穿通道则呈现细而密集的状态，击穿瞬间注入的能量小于0.1 Hz。

图6 不同频率余弦方波电压下针板电极缺陷的击穿通道形貌Fig.6 Morphology of needle plate electrode defects breakdown channel under cosine square wave voltage with different frequency

对于水树缺陷，0.1 Hz和0.5 Hz的余弦方波电压作用下击穿通道未发现显著的区别，击穿通道都呈现出细而密集的状态，其中0.1 Hz的余弦方波电压下典型水树缺陷的击穿通道如图7所示。

图7 0.1 Hz余弦方波电压的典型水树缺陷击穿通道的形貌Fig.7 Morphology of typical water tree defect breakdown channel at 0.1 Hz cosine square wave voltage

2.4 余弦方波电压频率作用下的击穿时刻

通过对余弦方波击穿电压波形的统计发现，绝大多数击穿发生在电压的极性变换阶段也就是余弦方波的上升沿或下降沿的位置。对于0.1 Hz的余弦方波电压，上升沿或下降沿的位置都观测到有击穿发生，极少部分的试样击穿发生在正直流阶段。而对于0.5 Hz和1.0 Hz的余弦方波电压，试验中的所有击穿均发生在由正极性转换为负极性下降沿的位置。出现这种现象的原因在于，缺陷在极性变换阶段，电压发生瞬间反转，增大了缺陷中的实际电场，因而容易导致击穿。而对于0.5 Hz和1.0 Hz的余弦方波电压试验中的所有击穿均发生在由正极性转换为负极性下降沿的位置，是由于空间电荷注入的极性和数量的不同而导致。电荷注入会降低缺陷位置的实际电场强度，而正电荷注入的速度远低于负电荷[21]，使得正极性阶段注入缺陷位置的空间电荷数量较少，实际电场强度下降少，极性反转到负极性过程中合成电场强度大于负极性反转到正极性的过程。

3 讨论

以0.1 Hz和0.5 Hz的余弦方波为例进行比较。通过试验可知，在两种典型缺陷模型下，0.5 Hz余弦方波的击穿时间均短于0.1 Hz余弦方波。经仿真计算，两种模型缺陷位置的场强均远大于30 kV/mm的XLPE材料的空间电荷注入场强[22]，导致空间电荷的注入，从而会显著降低缺陷位置的实际场强。0.1 Hz余弦方波的直流阶段为5 s，长于0.5 Hz的余弦方波的直流阶段（1 s），因而0.1 Hz余弦方波注入的电荷量也应多于0.5 Hz余弦方波，导致在幅值相同的条件下，0.1 Hz余弦方波引起的实际场强低于0.5 Hz余弦方波。

空间电荷的注入受电场强度和作用时间的共同影响。由于缺陷位置的场强很高，尽管电荷注入的时间仅为0.5～5.0 s，也会有较为可观的空间电荷注入，从而会显著降低缺陷位置的实际场强。但在极性变换阶段，缺陷上的电压发生反转与上一极性电压作用下注入的空间电荷形成电场叠加，增大了缺陷中的实际场强[23]。尽管0.5 Hz余弦方波注入的电荷量少于0.1 Hz余弦方波，最大的合成场强可能低于0.1 Hz余弦方波，但单位时间内极性变换的次数多于0.1 Hz余弦方波。两种频率在缺陷处的合成场强示意如图8所示。在合成强度和电压频率因素的共同作用下，使得0.5 Hz余弦方波电压作用缺陷的击穿时间短于0.1 Hz余弦方波电压的击穿时间。因而，对于工程实际来说，增大余弦方波试验电压的频率可有效地加强耐压考核的强度，提高耐压试验的效率，可以针对0.5 Hz和1.0 Hz的余弦方波制定对应的耐压试验考核时间。