一种基于交叉熵的top-k频繁项集挖掘算法

2022-04-25郑川龙

郑州大学学报（理学版） 2022年4期

宋威，郑川龙

(北方工业大学信息学院北京 100144)

0 引言

作为数据挖掘[1-2]的主要研究问题之一，频繁项集[3-4]旨在发现那些支持度不低于用户指定阈值的所有项目。如何设置合适的阈值，一直是频繁项集挖掘面临的难题之一。为解决这一问题，学者们提出了挖掘top-k频繁项集[5-6]的问题，即发现支持度最高的k个频繁项集。这类问题通过设置更易理解的结果项集数量k，来取代最小支持度阈值，更适合于非领域专家的用户使用，并已在若干领域得到了应用[7]。TopKRules[6]是一种挖掘top-k关联规则的方法，挖掘top-k频繁项集可以看作是TopKRules方法2个阶段中的第1个阶段。top-kMiner算法[8]使用2-频繁项集产生更长的候选项集，再从候选项集中得到真正的top-k频繁项集。BTK[9-10]算法用频繁项集挖掘中的包含索引结构来提高挖掘效率。TKFIM算法[11]利用集合论方法，特别是等价类技术来挖掘top-k频繁项集。这些方法均使用树或列表来转换原始数据，并通过逐步过滤不可能产生最终结果的项集来加快搜索空间的遍历。由于需要不断保存与更新中间结果，计算开销较大仍然是此类问题最大的挑战。

由于能快速挖掘到可接受的近似结果，利用启发式方法来挖掘项集的研究正在兴起，如GA-Apriori[12]、HUIM-ABC[13]、HUIM-SPSO[14]等方法。这类方法不需要额外的数据结构，通过模拟生物群体或物理现象来挖掘近似的项集，不但易于实现，而且具有较高的挖掘效率。据我们所知，目前尚没有基于启发式方法的top-k频繁项集挖掘的工作。

交叉熵(cross entropy, CE)方法[15]是基于概率模型采样生成试探解的全局优化算法，通过更新概率分布模型，不断优化群体中解的质量，这与挖掘top-k频繁项集的本质是一致的。因此，本文提出了一种基于交叉熵的top-k频繁项集挖掘算法(top-kfrequent itemset mining algorithm based on cross entropy,KCE)。

KCE算法用位图来转换原始数据和项集，并直接使用项集的支持度作为优化函数。在概率向量的更新过程中，KCE算法确保了支持度高的项目在后续迭代中出现的概率更大。为了约简搜索空间，KCE算法提出了过滤支持度的概念，从一开始就避免搜索那些不可能出现在结果中的项目。此外，KCE算法提出了按位交叉策略，提高了样本的多样性，有助于发现更为精确的结果。实验结果表明，KCE算法具有挖掘效率较高，存储开销较小的优势，且可以发现绝大多数精确的top-k频繁项集。

1 问题描述

1.1 top-k频繁项集挖掘

设IS={i1,i2,…,im}是项目(item)的集合，α⊆IS称作项集(itemset)。设TDB={T1,T2, …,Tn}是事务数据库，每条事务Td∈TDB(1≤d≤n)是一个项集，拥有唯一的标识d。若项集α⊆Td，则称事务Td包含α。

事务数据库TDB中包含项集α的事务数称为α的支持度，定义为

σ(α)=|{Tq|α⊆Tq∧Tq∈TDB}|。

(1)

若支持度高于项集α的项集不超过k个，则α就是一个top-k频繁项集。所谓top-k频繁项集挖掘就是找出事务数据库中支持度最高的前k个项集。

与普通的频繁项集挖掘任务不同，挖掘top-k频繁项集不需要用户指定最小支持度阈值，或者也可以说是将最小支持度阈值设置为0。这就意味着对于同样的事务数据库，top-k频繁项集挖掘比一般的频繁项集挖掘需要遍历更大的搜索空间，计算开销更为巨大。

本文将使用示例数据库EDB={(T1：A，B，C，E), (T2：B，C，F), (T3：D，E), (T4：A，B，C，D，E), (T5：C，E)}，来对概念和算法做解释说明。该数据库由5条事务组成，如(T1：A，B，C，E)表示事务T1，该事务由4个项目A、B、C、E组成。项集{CE}分别出现在事务T1、T4以及T5中，故其支持度σ(CE)=3。为简便起见，本文后续的描述中均省略项集的括号，如将{CE}记为CE。示例数据库中，top-5频繁项集为{C: 4,E: 4,B: 3,BC: 3,CE: 3}，其中冒号后面的数值代表项集的支持度。

1.2 交叉熵方法

交叉熵方法既可以用于估计复杂随机网络中罕见事件的概率，也可用于解决复杂的组合优化问题(combinatorial optimization problem, COP)。在本文中，我们利用交叉熵解决COP的思路来挖掘top-k频繁项集。

经典的交叉熵方法解决COP所使用的向量定义如下。假设Y=(y1,y2,…,yn)是一个n维二进制向量。交叉熵的目标是使用随机搜索算法，通过最大化函数S(X)的值，来重构未知向量Y，

(2)

使S(X)=n的直接方法便是不断生成不同的二进制样本向量X=(x1,x2,…,xn)，使其等于向量Y。在交叉熵方法中，我们使用随机伯努利分布来产生这些不同的样本向量X，并使用概率向量P=(p1,p2,…,pn)来记录每轮更新后不同样本向量中每个元素出现的概率，经过不断的迭代更新后，概率向量P的不同位将稳定为0或1，从而使由P确定的样本向量收敛，得到最优解。

交叉熵方法首先随机初始化概率向量P0=(1/2, 1/2,…, 1/2)，然后采用随机伯努利方法产生不同的样本向量X1，X2，…，XN，再根据一定的评判标准，在样本中计算适应度函数S(Xi)。这里假设γt是样本的ρ分位点所对应的数值，记为

γt=S(X「N×ρ⎤)，

(3)

其中:「N×ρ⎤表示不小于N×ρ的最小整数。我们把目标函数值位于总体样本ρ分位点内的所有向量Xi所构成的样本称为精英样本Se，即

Se={Xi|S(Xi)≥γt}。

(4)

再使用公式(5)更新概率向量的每一位，

(5)

其中：j=1, 2, …,n；Xi=(xi1,xi2, …,xin)；t是迭代次数；I(·)是指示函数。

(6)

其中E是一个事件。

交叉熵方法使用公式(5)不断更新概率向量，并根据概率向量更新样本向量，直到满足终止条件为止。终止条件一般是分位值γt稳定不变，或者概率向量趋于二进制向量。

2 KCE算法

2.1 项集信息的位图表示

位图是项集挖掘中常用的数据结构，具有存储开销小，便于使用高效位操作的优势。在KCE算法中，我们使用位图来转换原始的事务数据库。位图中的每个元素由公式(7)计算得到，

(7)

其中：ik代表第k个项目；Tj代表第j个事务。由公式(7)可知：若ik出现在Tj中，则第j行第k列的位图元素值取1；否则取0。

表1是示例数据库EDB的位图表示。例如，项目A出现在T1和T4中，故A的位图表示为Bt(A)=(10010)。同理，B的位图表示为Bt(B)=(11010)。如果我们要得到项集AB的位图，则只需对Bt(A)和Bt(B)做按位与运算，即Bt(AB)=Bt(A) &Bt(B)=(10010)。结果中含有两个“1”，表示项集AB的支持度为2。

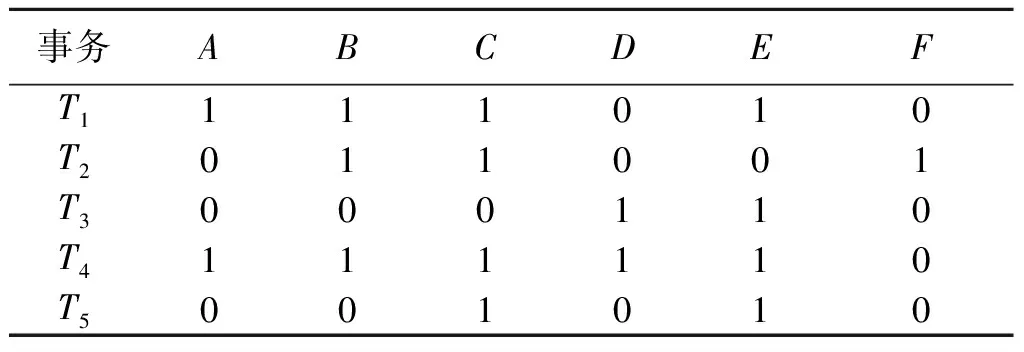
表1 示例数据库的位图表示Table 1 The bitmap representation of the example database

2.2 基于交叉熵的模型构建

在将数据库转换为位图之后，我们同样可以将项集用二进制向量来表示，称这种二进制向量为项集向量。

我们直接使用项集的支持度作为优化对象，即对于项集α，

S(α)=σ(α)。

(8)

在第t次迭代时，我们把N个项集向量按照S(Xi)的降序进行排序，并更新分位点γt的位置和概率向量Pt中每一位所对应的概率值。

2.3 剪枝策略

由于项集的支持度满足向下闭合性质，即：对任意两个项集α，β，若α⊆β，则σ(α)≥σ(β)。由此可知，若项集α不是top-k频繁项集，那么α的所有超集均不是top-k频繁项集；反之，若项集α是top-k频繁项集，那么α的所有子集也是top-k频繁项集[8-9]。这是top-k频繁项集挖掘中最基本的剪枝手段。KCE算法同样也使用了该剪枝策略。

基于启发式方法的项集挖掘算法，一般在开始阶段都会固定项集向量中包含的项目个数[12-13]。因此，在最初的搜索阶段就删去那些不可能出现在top-k频繁项集中的项目，可有效地约简搜索空间，提高挖掘效率。

定义1设ik∈IS，Sk={ix|σ(ix) >σ(ik)}，若|Sk|=k-1，则称σ(ik)为过滤支持度，记作σf，其中|Sk|代表集合Sk中项目的个数。

由定义1可知，数据库中过滤支持度即为支持度按由高到低顺序排列的第k个项目的支持度。

定理1若项集α的支持度小于过滤支持度σf，则α及其超集都不是top-k频繁项集。

证明假设σk是数据D中top-k频繁项集实际的最小支持度，根据定义1，有σf≤σk。

若σ(α)<σf，则σ(α)<σk，即α不是top-k频繁项集。

对∀β⊃α，有σ(β)≤σ(α)，故σ(β)<σk，即β也不是top-k频繁项集。

根据定理1，一旦确定某个项目的支持度低于过滤支持度，则该项目的所有超集均不可能在结果中出现。因此，该项目无须出现在算法的项集向量中。

考虑从示例数据库EDB中挖掘top-5频繁项集，可知σf=2。由于σ(F)=1<σf，故项集向量只包含A、B、C、D、E，而无须考虑项目F。

2.4 按位交叉策略

基于启发式方法挖掘频繁项集，很难保证在有限的迭代次数内完全得到精确的解，增加样本的多样性是解决这一问题的有效手段[13-14]。

为提高样本多样性，我们提出了项集向量的按位交叉策略，其核心思想是从精英样本Se中选一部分项集向量，按照交叉部分位的取值，而不是概率向量的方式，产生新的向量。具体而言，给定种群规模N和交叉系数δ(0<δ<1)，在每次产生的个体之中，⎣|Se|×δ」个新的项集向量由按位交叉策略产生，其余的N-⎣|Se|×δ」个新的项集向量由当前的概率向量产生，其中：|Se|代表精英样本的数量；⎣|Se|×δ」表示不超过|Se|×δ的最大整数。

对按位交叉策略，每次选取2个项集向量Vm和Vn，假设项集向量的长度为l，则先随机产生一个整数j(1≤j≤l)，再从l位中随机确定j位，记为b1，b2，…，bj，再将Vm和Vn中第b1位，b2位，…，和bj位的值互换，这样便产生了两个新的项集向量V′m和V′n。重复这种逐对按位交叉操作，直到随机选定的⎣|Se|×δ」个项集向量均处理完毕为止。

假设选定了两个项集向量V1=<11010>和V2=<00110>，通过产生随机数来确定二者的第1位和第2位作按位交叉，得到新的项集向量V′1=<00010>和V′2=<11110>。

2.5 算法描述

算法1KCE的总体流程。

输入：事务数据库TDB，结果数量k，种群规模N，分位点ρ，交叉比例δ，最大迭代次数miter。

输出： top-k频繁项集。

1) Initialization( )；

2) whilet≤miterandPt不是二进制向量 do

3) 由公式(5)计算Pt；

4) 随机选取⎣|Se|×δ」个项集向量，执行按位交叉操作；

5) 根据Pt产生剩余的N-⎣|Se|×δ」个项集向量；

6) 依据支持度由大到小的顺序排列样本，得到新一代群体，记为X1，X2，…，XN；

7) 更新top-k频繁项集；

8) 由公式(3)计算γt；

9)t++；

10) end while

11) 输出top-k频繁项集。

KCE算法首先调用过程Initialization(算法2所示)进行初始化。一次迭代过程中，首先更新概率向量，然后选取一部分精英样本执行按位交叉操作，再由概率向量产生其他的下一代项集向量，进而更新top-k频繁项集，增加迭代次数。重复以上迭代过程，直到达到循环结束条件为止。

算法2Initialization( )

1) 扫描一遍数据库，根据过滤支持度删去无效的项目；

2) 用二进制位图表示数据库；

3)P0=(1/2, 1/2, …, 1/2)；

4) 由P0产生第一代种群；

5) 依据支持度由大到小的顺序排列样本，记为X1，X2，…，XN；

6) 计算top-k频繁项集；

7) 由公式(3)计算γt；

8)t=1。

初始化过程首先根据定理1对项目进行剪枝，再将数据库转换为位图形式。概率向量的每个概率元素的初始值均设为0.5，并据此得到初始种群和初始top-k频繁项集。最后，将迭代次数设置为1。

3 实验验证

我们与TopKRules[6]和TKFIM[11]两种算法进行了实验对比，其中：TopKRules算法的代码由SPMF平台下载获得[16]，TKFIM算法的代码由文献[11]获得。TopKRules算法的挖掘结果是top-k关联规则，为公平对比，我们省略了该算法由项集产生规则所带来的计算开销。此外，TKFIM算法的代码只能处理每行列数相同的数据集，对Retail这种每条事务包含项目数不等的数据则无法处理。因此，在3.2节与3.3节的实验结果中，未报告TKFIM算法在Retail数据集上的效率与内存消耗。

3.1 实验环境和数据集

KCE算法使用Java语言实现，实验平台的配置为macOS 11.1操作系统、2.3 GHz 4核CPU和8 GB RAM。

使用4个数据集验证算法的性能，其中：T20I30D10k和T40I45D50k是由SPMF平台[16]提供的数据生成器产生的合成数据集；Chess和Retail为真实数据，由SPMF平台下载获得。数据集的参数特征如表2所示。

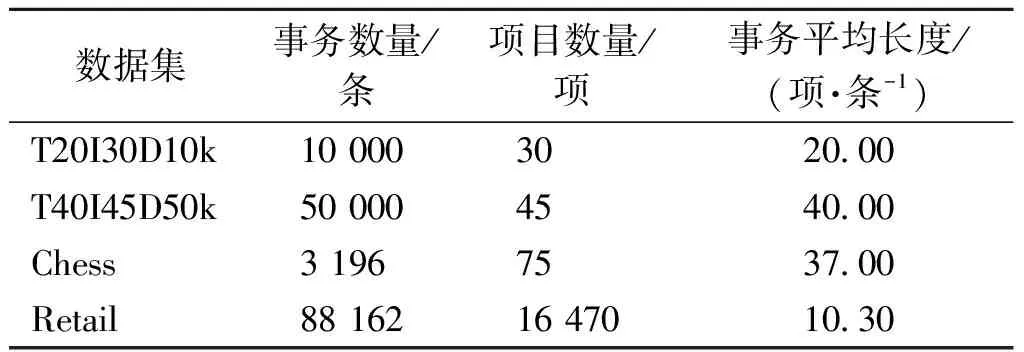
表2 数据集的特征Table 2 Characteristics of the dataset

对于所有的实验，我们设置每轮迭代的样本的大小N为2 000，分位点ρ为0.2，交叉系数δ为0.2，最大迭代次数miter为2 000。

3.2 时间消耗

图1展示了k取不同值时，3种算法在4个数据集上运行时间的对比，图1(b)、(c)纵坐标T为时间变量取对数后的结果。

图1 时间消耗比较Figure 1 Time consumption comparison

由图1可知，算法TKFIM的效率最低。这主要是由于TKFIM算法基于等价类的思想，通过反复对包含项集的事务集合作交运算，来维护临时的top-k频繁项集。除支持度和包含项集的事务差异之外，缺少更为高效的剪枝策略。

除Chess数据集外，KCE的运行时间始终优于TopKRules。KCE算法在Chess数据集上的运行时间不如TopKRules的原因在于，该数据集的规模非常小，仅有3 196条数据和75个不同的项目。启发式算法用于构建向量、计算过滤支持度、执行按位交叉策略的时间，反而超过了这些策略所能节约的时间。反之，当数据集较大时，如Retail数据集上，k取100时，使用过滤支持度可以在挖掘初期就删去16 370个不可能产生最终结果的项目，从而大大约简了搜索空间，提高了挖掘效率。

3.3 内存开销

3种算法的内存开销比较结果如图2所示。3种算法的内存开销与运行时间对比结果一致。TKFIM算法的内存开销依然最高，这主要是其使用的top-k列表结构需要保存大量中间结果而造成的。

图2 内存开销比较Figure 2 Memory consumption comparison

尽管KCE同样在Chess数据集上比TopKRules消耗了更多的内存。但随着k值的不断增加，二者之间的差距呈现了逐步减少的趋势。特别是当k取100时，KCE与TopKRules的内存消耗几乎完全一致。在其他3个数据集上，KCE的整体内存消耗均优于TopKRules。特别是在较大的数据集Retail上优势较为明显，由于过滤支持度在初始阶段就删去了大量不可能出现在最终结果内的项目，KCE在Retail数据集上内存消耗量平均是TopKRules内存消耗量的23.07%。

此外，相对于TopKRules而言，KCE的内存消耗总体上呈现出了较为平稳的趋势。这证明了基于启发式方法挖掘频繁项集无须建立额外的树或列表结构，一旦确定了向量的大小，开始了迭代挖掘，内存总体消耗就基本可以确定了。

3.4 精度测量

考虑到启发式top-k频繁项集挖掘算法无法保证在一定的迭代次数之内找到所有准确的结果。我们用来度量KCE方法的精度公式为

Ck/k×100%，

(9)

其中：Ck是KCE挖掘到的真实top-k频繁项集的数量。而实际的top-k频繁项集由精确算法TopKRules挖掘得到。

与3.2节和3.3节一样，我们在每个数据集上取5组不同的k值，共进行了20次实验。其中：KCE算法在T20I30D10k上的5次实验均能找到全部正确结果，而在T40I45D50k、Chess和Retail数据集上能找到全部正确结果的次数分别为4次、4次和2次。也就是说，在20次实验中，KCE算法能够得到全部正确结果的次数为15次，占总实验次数的75%；而且所有结果的精度均在90%以上。