基于SOLO分类理论的高考数学试题研究

陈小红，周锦程，石定埔，潘掖雪

（1.黔南民族师范学院 数学与统计学院，贵州 都匀558000；2.黔南民族师范学院 计算机与信息学院，贵州 都匀558000；3.黔南州复杂系统与智能优化重点实验室，贵州 都匀558000；4.黔南民族师范学院附属中学，贵州 都匀558000）

0 引言

高考不仅承载着科学的人才选拔功能，还对人才培养具有导向性的作用.当前，关于高考数学试题的评价，主要集中在数学试题中知识点的多少、难度及能力结构等方面，但关于高考数学试题思维层次方面的研究较少.基于皮亚杰的认知发展阶段理论，澳大利亚著名教育心理学家比格斯（Biggs）和卡利斯（Collis）在20 世纪80 年代建立了SOLO（Structure of the Observed Learning Outcome）分类理论.该理论是一种以等级描述为特征的质性评价方法.吴维宁［1］将SOLO 分类理论引入中国，介绍了SOLO 分类法的由来并将其用于学生的成绩评价中；李兆祥［2］阐明该理论可用于学生的思维评价；蔡永红［3］系统地对SOLO分类理论的起源以及它的主要内容进行了论述.

2006 年广东省历史学科最先将SOLO 分类理论用于高考命题［4］；曾建国［5］基于SOLO 理论并以三角函数模块为例，从知识点考查的视角对高考数学试题进行了评价研究；艾珲琏等［6］基于SOLO 分类理论对2016年全国卷高考数学试题进行思维层次分析发现：2016年的3份全国高考数学试卷整体的思维层次介于多点结构和关联结构之间；王亚婷等［7］基于SOLO 分类理论对2019 年高考数学全国卷进行试题思维层次分析发现：全国卷强调学生知识的基础性和综合性，试题思维层次侧重多点结构与关联结构；教育部考试中心（2019）［8］分析了2019年高考数学试题的变化以及对学生各方面的要求；教育部考试中心（2020）［9］针对2020年高考数学试题进行评析，揭示了高考命题与现实生活情景紧密相连.

随着SOLO分类理论研究的深入，越来越多的研究者开始关注将SOLO分类理论用于各种试题的思维层次评价中.因此，本文利用SOLO分类理论，以2016—2020年全国高考数学III卷（理科）和2021年全国高考数学甲卷（理科）为例（以下简称2016—2021年卷），从思维层次角度对高考数学试题进行研究.

1 研究设计

1.1 研究对象

本文选取2016—2020年理科数学普通高等学校招生全国统一性考试·全国III卷（以下简称全国III卷）以及2021 年全国甲卷理科数学作为研究对象.全国III 卷起于2016 年，其产生的根本原因是为了符合当前社会的需要和促进教育的公平与公正.2021年作为落实中共中央、国务院印发的《深化新时代教育评价改革总体方案》的开局之年，2021年无全国III卷，以往使用全国III卷的贵州、云南、四川、广西和西藏2021年则使用全国甲卷，故本文在2021年高考理科数学中选取2021年全国甲卷作为研究对象.

1.2 研究工具

SOLO被称为可观察到的学习结果的结构，它是一种以等级描述为特征的质性评价理论.SOLO分类理论能较好地评价学生思维能力所达到的深度和广度，它将学生的思维层次水平划分为前结构（P）、单点结构（U）、多点结构（M）、关联结构（R）和抽象拓展结构（E）五个从低到高的思维层次.SOLO 分类理论既能考虑到对学生知识量的评价，又能考虑到对学生学习质量的评价.

2 研究过程

2.1 试题SOLO层次划分

参考高凌飚等［10］主译的《评价学习的质量——SOLO 分类法》中认知发展的基本阶段和回答层级描述表，前结构表现出的能力为最低，问题线索和答案混淆，回答不存在逻辑的联系，回答包括三种情况：拒绝、同义反复和瞎说瞎撞.基于高考命题特点，前结构不符合高考命题的基本原则.因此，本文在进行划分试题SOLO层次时，将2016—2021年卷试题思维层次划分为单点结构（U）、多点结构（M）、关联结构（R）和抽象拓展结构（E）.

根据高考数学试题结构的特点，在SOLO 分类理论的基础上，本文参照周莹等［11］SOLO 层次划分方法，对2016—2021 年卷SOLO 层次从低到高进行划分以及对应试题难度从低到高进行界定，如表1所示.

表1 基于SOLO分类理论的试题思维层次划分表

2.2 试题内容的领域划分

参考《普通高中数学课程标准（2017年版）》［12］（以下简称《标准》）中高中数学课程的划分，将高中课程分为预备知识、函数、几何与代数、概率与统计、数学建模活动与数学探究活动五个主题，其中，预备知识属于必修课程，其余四个主题贯穿于必修课程和选择性必修课程之中.由于高考的特殊性，对数学建模活动与数学探究活动暂时无知识性考查，故暂不作分析.对2016—2021年卷进行分析，发现高考从知识、能力以及个性品质三个方面，以知识为基础，以问题为载体通过必考和选考对理工类学生进行考查，试题内容划分如表2所示.

表2 试题考查内容划分表

3 分析与讨论

确定试题思维层次和考查内容划分规则后，对2016—2021 年卷每道试题进行划分.对于思维层次界限模糊的试题作如下说明：（1）对于介于多点结构与关联结构以及关联结构与抽象拓展结构之间的试题，将综合考虑计算过程的复杂程度和试题所涉及的知识点个数等方面来进行划分；（2）当一道题的每小问涉及的知识领域不同时，将其单独划分，分值也将单独计算；（3）当一道题每小问处于不同的SOLO层次而考查的知识为同一知识领域时，以最高层次划分.

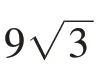
试题分析：本题主要考查三棱锥的相关知识，涉及的知识点有三角形面积、球的半径、三棱锥的体积.对学生空间想象能力、求解运算能力要求较高，将其划分为关联结构.

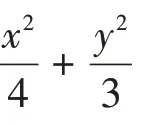
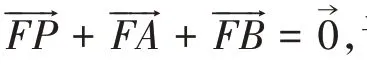
试题分析：本题主要考查直线与椭圆的位置关系以及等差数列的证明.第（1）问属于几何与代数知识，试题情景常见，思维层次要求不高，运算过程简单，故划分为多点结构；第（2）问属于函数领域知识，试题情景常见，需要进行推导，思维层次要求较高，计算过程较复杂，故划分为关联结构.

3.1 2016—2021年卷“内容领域与SOLO层次”的二维评价分析

按照表1～2 对2016—2021 年高考试题进行试题题号与考查内容分析.对试题进行“试题思维层次与考查内容”二维表划分，如表3～8所示，并从内容领域、题型类别以及SOLO思维层次三个方面进行分析与讨论.

表3 2016年卷“内容领域与SOLO层次”划分二维表

3.1.1 内容领域方面

由于2016 年首次出现全国III 卷，它在题量上略多于其他五套卷，具体区别表现：2016 年卷有三道解答题属于选择性必修课程，其中两道属于几何与代数主题，一道属于预备知识主题，2017—2021年卷均只有两道解答题属于选择性必修课程，一道属于几何与代数主题，一道属于预备知识主题.

表4 2017年卷“内容领域与SOLO层次”划分二维表

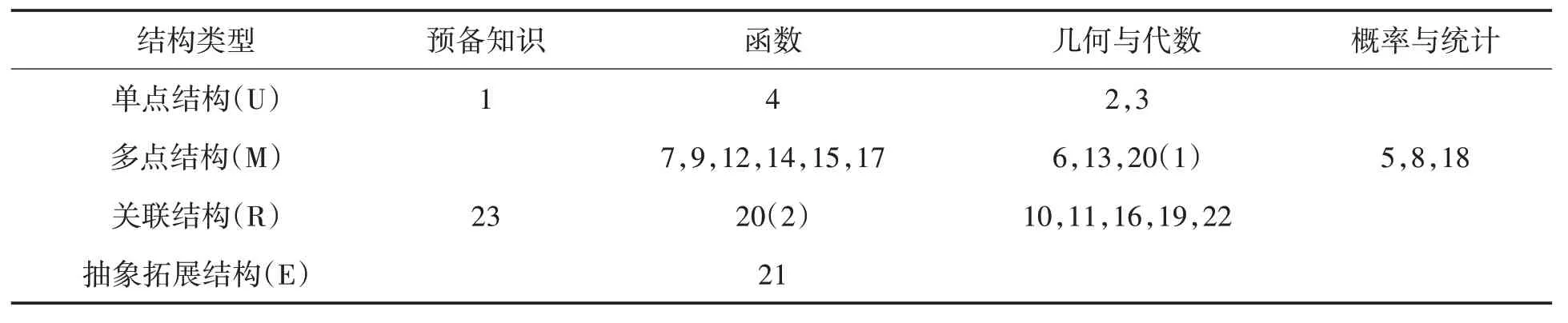
表5 2018年卷“内容领域与SOLO层次”划分二维表

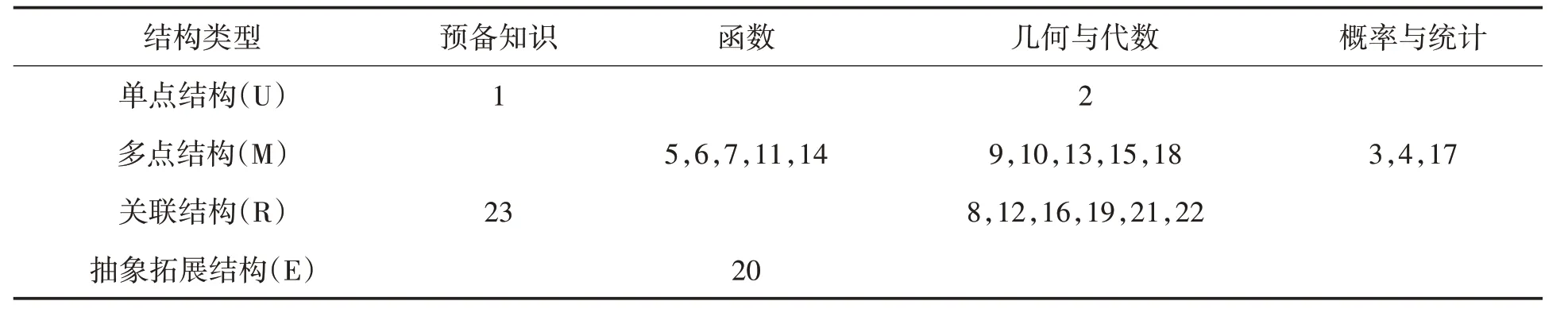
表6 2019年卷“内容领域与SOLO层次”划分二维表

表7 2020年卷“内容领域与SOLO层次”划分二维表

表8 2021年卷“内容领域与SOLO层次”划分二维表

3.1.2 试题题型方面

六套试卷在某些相同题号所考查的内容和形式一致，设计有规律，能够初步看出高频考点.例如，第（1）题和第（2）题均以选择题的方式考查预备知识主题内容和几何与代数主题内容，第（19）题与第（22）题都以解答题的方式考查几何与代数主题知识；除2016 年卷外，其余五套卷第（23）题都以解答题的方式考查预备知识主题知识；值得注意的一点是，以解答题的方式考查概率与统计主题知识在2016年卷、2017 年卷、2018 年卷中都是第（18）题，而2019 年卷和2021 年卷则改变其规律将其放在第（17）题；2019年卷第（21）题是对几何与代数主题知识的考查，其他五份试卷都是对函数主题知识的考查.

3.1.3 试题思维层次方面

六套试卷具有同样特征：对多点结构（M）和关联结构（R）的考查较多，对单点结构（U）和抽象拓展结构（E）的考查相对较少.每个题型的试题思维层次从低到高，循序渐进，符合学生的认知发展规律，如表3～8所示.

3.2 2016—2021年卷试题相关分值统计分析

2016—2021年卷总分值为150分，其中，选择题共计12小题（每小题5分，总计60分），填空题共计4小题（每小题5分，共计20分），解答题共6题（17～21题为必考题，每小题12分；22、23为选考题，每小题10 分，共计70 分）.由于解答题各小问所考查的知识点领域以及SOLO 层次不同，第一问较为简单，定为5 分，第二问较为复杂，定为7 分.其中2016—2021 年卷选考题区分度以及难度相当，SOLO 思维层次属于多点结构，考查内容固定不变，因此不参与分值统计.

3.2.1 2016—2021年卷SOLO层次分值统计

根据表3～8绘制出2016—2021年卷SOLO 层次分值统计图，如图1所示，进一步探讨2016—2021年卷内容结构特点以及试题趋势，从而预测全国卷命题对SOLO层次的考查走向.

由图1 可知，2016—2021 年卷对试题SOLO 层次的考查有侧重点，且多点结构＞关联结构＞单点结构＞抽象拓展结构，2016—2021 年卷试题思维层次侧重分布在多点结构，其次是关联结构；除2017 年卷和2021 年卷有两道抽象拓展结构的试题外，2016 年卷、2018 年卷、2019 年卷和2020 年卷的共同点是均有一道抽象拓展结构的试题，且题型都是解答题.总体来看，2016—2021年卷的试题思维层次多处于多点结构，并且题型、结构和难度总体保持稳定；2016—2021 年卷均对四个水平结构进行考查，有利于全面考查学生的思维层次水平.

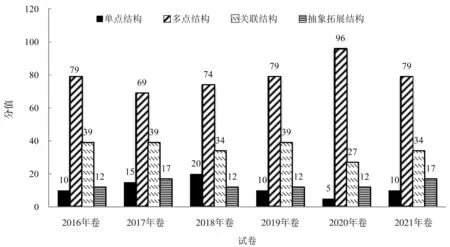
图1 2016—2021年卷SOLO层次分值统计图

3.2.2 2016—2021年卷知识点领域分值统计

根据表3～8 绘制出2016—2021 年卷知识点分值统计图，如图2 所示，探讨2016—2021 年卷对知识领域的考查力度.

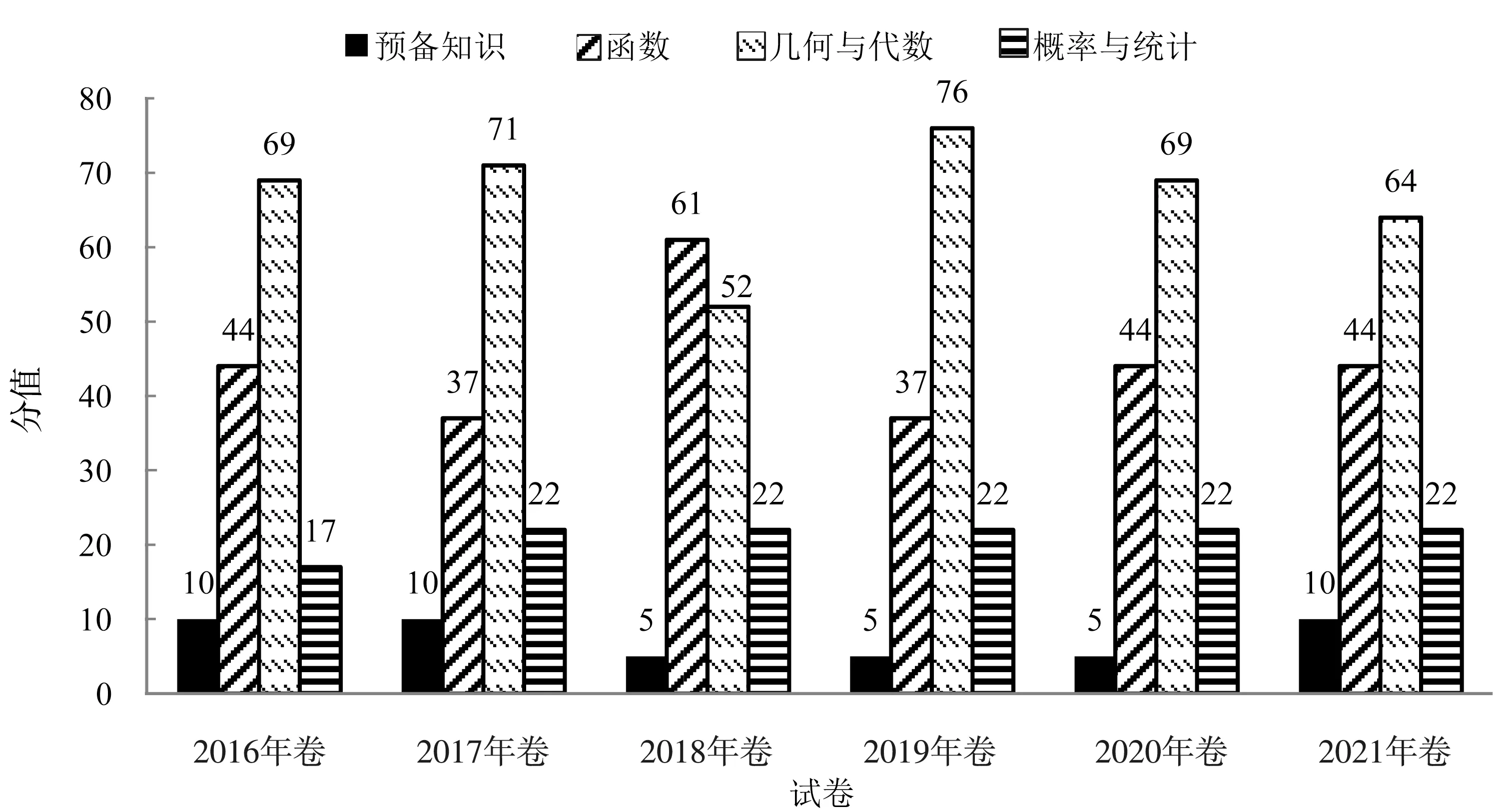
图2 2016—2021年卷知识点分值统计图

由图2可知，试题对各个领域均有考查，分值的设置有层次.从分值来看，2016年卷、2017年卷、2019年卷、2020 年卷和2021 年卷对几何与代数主题的知识考查力度最大，所占分值比例最高，特别是2019年卷，峰值点达到76，而2018年卷对函数主题知识考查力度最大，几何与代数主题知识次之.总体而言，2016—2021 年卷对预备知识主题知识的考查力度较小，对概率与统计内容的考查相对稳定，2016 年卷设置一道选择题和一道解答题，2017—2021 年卷均设置两道选择题和一道解答题；2016—2021 年卷连续六年以选择题的方式考查集合和复数，可见集合和复数是高频考点；2017—2019 年卷连续三年以选择题的方式考查二项式的应用，可见二项式是一个高频考点.从分值变化幅度上看，分值变化主要集中在函数主题和几何与代数主题上，因此，可看出全国III卷和全国甲卷对知识领域的考查轻重分明，各域齐抓.

4 结论与建议

4.1 研究结论

4.1.1 坚持改革，稳重有变

通过对2016—2021年卷试题思维层次的统计分析，发现六份试卷试题思维层次多处于多点结构和关联结构，单点结构和抽象拓展结构相对较少.整套试题主要考查中档难度试题，对简单题和难题的考查较少，符合高考命题改革原则，使高考不仅是服务于高校选拔，更是立德树人的重要载体.此外，解答题在内容和顺序上具有一定的规律，但不是一成不变.例如，2016 年卷、2017 年卷、2018 年卷和2020 年卷在解答题部分对概率与统计主题的知识考查都放在第（18）题的位置，而2019年卷和2021年卷则是放在第（17）题.从这一点来看，试题对考查内容的位置进行了轻微的调整.这同时也说明，在整体符合考试大纲及考试说明的前提下，部分内容的布局和难度可以进行调整，这种调整有助于学生全面掌握重点知识和重点内容，破解僵化的应试教育.

4.1.2 坚持开放创新，考查关键能力

通过对2016—2021年卷试题思维层次的统计分析，从整体上来说，第（1）题～第（10）题思维层次均处于单点结构和多点结构，相对容易；第（13）题、第（14）题、第（17）题和第（18）题思维层次多处于多点结构；第（11）题、第（15）题、第（16）题、第（19）题和第（20）题的思维层次多处于关联结构；第（21）题的思维层次多处于抽象拓展结构.可以看出六套试卷均贯彻“低起点、多层次，高落差”的科学调控原则，对学生思维层次的考查稳定，试题结构层次分明，面向全体学生.但是，在整体稳定的过程中，也不缺乏创新.例如，在高考改革的大环境下，结构不良问题的适度开放，2021 年卷改变以往只出现结构良好问题的规律，在第（18）题出现结构不良问题，相比结构良好的问题，结构不良问题具有开放性，能够有效考查学生构建数学问题、分析问题以及解决问题的能力.

4.2 教学建议

4.2.1 以课程标准为基点，深入研究教材

通过“试题思维层次与考查内容”二维表可以看出，高考试题思维层次分布为：多点结构＞关联结构＞抽象拓展结构＞单点结构；从分值上看，对抽象拓展结构的考查与单点结构的考查总体分值趋于稳定，变化幅度小；从知识领域上看，试题的命制重视对学生知识的基础性、综合性以及全面性的考查.因此，教师在教学中，首先，以课程标准为基点，深入剖析教材，从学生的角度分析教材制订的初衷；其次，运用教材使学生掌握的知识实现从无到有；最后，教学过程应该符合学生的认知规律，注重学生对基础知识的掌握和运用.例如，在椭圆及其标准方程这一节中，教材通过“节引言”提出问题，引导学生明白本节课的学习目标，利用“探究”栏目提出问题，引导学生探究椭圆的几何特征，为学习椭圆的概念和性质奠定基础.以“思考”栏目引导学生思考如何利用椭圆的几何性质建立合理的直角坐标系.在学生得到椭圆方程以后，利用第二个“思考”栏目，借助勾股定理引导学生理解引入b2的合理性，进而得到椭圆的标准方程.因此，在教学时，教师应该认真剖析《标准》和教材，根据教材内容系列化的设置，对学生进行层层递进的提问、引导，形成环环相扣的教学活动，使学生充分参与探究知识的发生和发展过程中.

4.2.2 淡化解题技巧，重视对理性思维能力的培养

高考数学强调理性思维，而逻辑思维能力是理性思维的重要体现.用SOLO 分类理论对2016—2021年卷进行试题思维层次分析，发现每套试题对单点结构、多点结构、关联结构和抽象拓展结构皆有考查，且考查逻辑思维能力的题型也在不断创新.在以往的教学中，部分教师重计算结果而轻思维分析过程，以技能训练代替思维分析.如此一来，学生会产生思维定势，不能深入思考问题.因此，在教学过程中，教师要注重对学生逻辑思维能力的培养，以学生的学习质量为出发点，对数学知识间的逻辑关系进行分析，使用SOLO 分类理论评价学生的学习效果，促进学生逻辑思维能力的提高.例如，在进行三角恒等变换的教学时，在学生学习诱导公式和两角差的余弦公式之后，根据学生所在的思维层次进行两角和与差的正弦、余弦、正切公式的教学，引导学生厘清各公式之间的内部逻辑关系.

4.2.3 立足基础知识，重视数学思想方法的渗透

通过分析2016—2021 年卷试题思维层次发现，多点结构所占分值最高，并且高考试题利用数学思想方法对分散的知识点进行整合，考查学生对数学知识的掌握程度，尤其是对学生数学知识的基础性、综合性以及全面性的考查.学生的思维层次从单点结构提升到抽象拓展结构，需要利用数学思想方法将分散的知识点进行“黏合”，而数学思想方法是伴随着知识的学习而逐渐培养起来的.因此，在教学中，教师应该立足于基础知识，注重数学思想方法的渗透，对分散的知识点进行整合，找到知识点之间的内部联系，让学生在学习的过程中领悟数学基本思想、积累数学基本经验.例如，教师在进行分段函数的教学时，先引导学生画出函数y= |x|的函数图像，再通过讨论与分类，将数学思想方法融入课堂教学中，对学生进行数形结合、分类与整合思想的渗透.