信号交叉口非机动车速度与流量关系研究
2022-04-24朱普周段宇洲杨森森
朱普周,段宇洲,杨森森
(1.河南工业大学 土木工程学院,河南 郑州 450001;2.长春工程学院 管理学院,吉林 长春 130021)
随着我国经济水平的不断提高,城市交通拥堵现象日益增多,其中非机动车道内自行车及电动自行车造成的拥堵现象也日益严重。为此,国内外学者进行了大量的研究,其中贾顺平[1-2]等通过实地调查,分析了电动自行车交通流三参数之间的关系,对非机动车进行了定量分析;孙明正等[3]在大量实测数据的基础上,对信号控制交叉口作为间断流交通运行特征的自行车流展开了较为深入的研究,分析了自行车的膨胀特性;周晨静等[4]分析了信号交叉口自行车对临近车道机动车通行能力的影响;Schleinitz等[5]发现不同类型的电动自行车与人力自行车的平均行驶速度有显著差异;徐程[6-7]等针对传统自行车和电动自行车混行路段,构建了基于高斯混合模型的速度分布函数,并通过引入机动车速度-密度关系模型,提出了非机动车交通流速度-密度关系模型。
本文在前人研究的基础上,通过信号交叉口非机动车交通数据的调查与分析,研究信号交叉口非机动车速度与流量的关系,为非机动车交通流的研究提供思路,以减少交通冲突与拥堵。
1 数据采集与处理
1.1 数据的采集
利用Adobe After Effects CS4软件,设定数据提取精度为25帧/s,时间精度为0.04 s,于2019年4月22日—26日共5个工作日的下午5:30—6:30的交通高峰时期,对郑州市区黄河路与花园路、纬五路与花园路的两个交叉路口进行数据提取,获得了两个信号交叉口非机动车流量、速度等数据。所调查的两个信号交叉口南北方向禁止机动车、非机动车左转,其中花园路与黄河路交叉口示意图如图1所示。

图1 花园路与黄河路交叉口示意图Fig.1 Schematic diagram of the intersection of Huayuan Road and Huanghe Road
1.2 数据的处理
在交通流参数统计时,经常使用车辆换算系数这一概念,车辆换算系数是指交通流中各类车型化为标准车的当量值。因此对于非机动车,其换算系数即为相同道路条件下单位电动自行车等效于单位自行车的数量。关于非机动车换算系数,叶晓飞等[8]基于有效面积和冲突事件模型提出两种计算模型,最终得到电动自行车的换算系数为1.229 5;徐兴等[9]结合非机动车有效行驶面积计算模型与超车率法,最终得出电动自行车对自行车的换算系数为1.346 2。从上述研究可以看到,电动自行车对自行车的换算系数都大于1.2且小于1.4,因此本文参考上述文献最终选定电动自行车对自行车的换算系数为1.3。
2 评价指标
2.1 流量指标
由于不同宽度的非机动车道,非机动车的通行能力是不同的[10]。参照机动车流量定义,非机动车流量定义为单位时间内通过单位宽度非机动车道的非机动车数量,即[11]
(1)
式中:q为非机动车流量,辆/(s·m);Q为特定区域单位时间内通过非机动车道的车辆,辆;W为非机动车道的宽度,m;t为调查时间,s。
2.2 饱和流率指标
非机动车群通过信号交叉口时,受到信号灯的影响,集群性比较明显。当绿灯刚刚启亮,非机动车以饱和流率释放,不规则地行驶在非机动车道上。由于不同宽度的非机动车道,饱和通过的非机动车流量是不同的,由此可将非机动车的饱和流率定义为单位时间内单位宽度的非机动车道饱和释放的非机动车数量。
绿灯刚启亮时,信号交叉口停车线处的非机动车以饱和状态完全释放,一般按照10 s的时间来计算饱和通过的非机动车数量。根据信号交叉口非机动车道的宽度,结合文献[12]交通流研究与机动车交通流调查方法,非机动车饱和流率的计算公式为[11]:
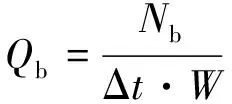
(2)
式中:Qb为非机动车饱和流率,辆/(s·m);Nb为非机动车以饱和状态通过信号交叉口的数量,辆;Δt为Nb辆非机动车以饱和状态通过信号交叉口所用的时间,s。
在实际计算非机动车饱和流率时,由于非机动车具有集群性,在绿灯前期的短时间内就会释放完成,因此通常选取高峰时段绿灯启亮5 s的时间内通过的非机动车辆作为调查对象;另外,由于非机动车骑行者在绿灯启亮前通常就会越过停车线占据到信号交叉口内,因此非机动车道宽度可以根据信号交叉口前排车辆实际占用的平均宽度确定。
2.3 速度指标
非机动车的速度主要指自行车与电动自行车混合下的各自速度,通常考察指标有区间速度和平均速度。
2.3.1 区间速度
区间速度指的是非机动车通过某一区间的速度,又称为行程车速,公式如下:
(3)
式中:vs为区间速度,m/s;t1、t2分别为非机动车驶入、驶出区间的时刻,s;L为该区间的距离,m。
2.3.2 平均速度
平均速度指的是非机动车行驶一定距离H与平均行驶时间的比值,如下式所示:
(4)
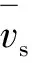
对不同类型非机动车分别进行统计,使用区间速度公式求取不同类型非机动车的速度;根据所求速度由平均速度公式得到不同类型非机动车间的速度差,以验证不同比例非机动车流对交通流的影响。
3 评价指标分析
3.1 非机动车流量结构
各信号交叉口非机动车流量如表1所示。由表1可以看出,信号交叉口电动自行车占非机动车总数的比例均在70%以上,其中花园路—黄河路南进口道的电动自行车所占比例为87.69%。

表1 信号交叉口不同类型非机动车流量构成Table 1 Composition of traffic flow of different types of non-motor vehicles at signalized intersections
3.2 非机动车饱和流率
高峰时段绿灯启亮5 s内通过信号交叉口4个进口道的非机动车数量如表2所示。由表2可以看出,非机动车饱和流率主要集中在0.76~0.97辆/(s·m),平均饱和流率为0.90辆/(s·m)。

表2 信号交叉口饱和流率统计表Table 2 Statistics of saturated flow rate at signalized intersections
3.3 非机动车速度
非机动车速度数据如表3所示,不同路段非机动车的速度分布如图2、图3所示。由表3可以看出:黄河路—花园路的自行车平均速度为12.81 km/h、85%位车速为16.52 km/h;电动自行车平均速度为19.39 km/h、85%位车速为24.47 km/h。纬五路—花园路的自行车平均速度为13.73 km/h、85%位车速为18.15 km/h;电动自行车平均速度21.17 km/h、85%位车速为25.94 m/h。显然,非机动车通过交叉口的速度差异较大,主要表现为:(1)电动自行车和自行车的平均速度差异较大,最大相差达7.44 km/h;(2)在绿灯中端或末端时,非机动车没有加速启动时间与非机动车群限制,速度较大,最大速度超过30 km/h。虽然如此,但是所调查信号交叉口电动自行车的85%位车速在25 km/h左右,基本满足最新政策规定的电动自行车限速到25 km/h的要求。

表3 非机动车速度特性 Table 3 Speed characteristics of non-motor vehicles
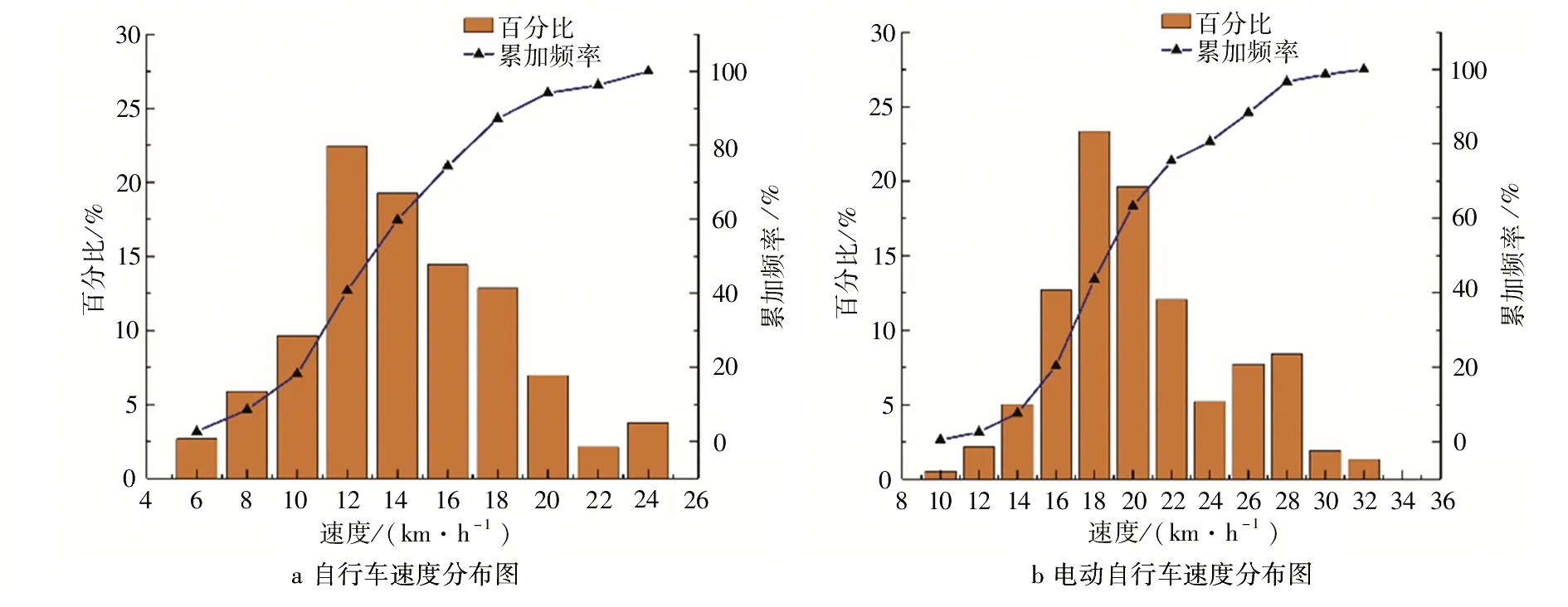
图2 花园路—黄河路不同类型非机动车速度分布情况Fig.2 The speed distribution of different types of non-motor vehicles on Huayuan Road-Huanghe Road
图3 花园路—纬五路不同类型非机动车速度分布情况Fig.3 The speed distribution of different types of non-motor vehicles on Huayuan Road-Weiwu Road
由图2、图3可以看出:约90%的自行车速度小于18 km/h,约90%的电动自行车速度小于26 km/h;相较于花园路—黄河路,花园路—纬五路上的非机动车速度较大,最大速度超过34 km/h。显然,这与两者的非机动车道的宽度和流量有着较大联系。
4 速度-流量模型
4.1 速度-流量模型构建
以花园路—黄河路为例进行速度-流量的回归分析。在回归分析之前要对电动自行车与自行车的流量进行统一化,即根据非机动车的不同换算系数,把两者进行统一化;然后再根据统一化的流量数据,得到花园路—黄河路信号交叉口非机动车的速度-流量散点图,如图4所示。分析图4,发现其速度-流量之间具有明显的幂函数关系,因此建立数学模型如下:
vu=a1Sa2
(5)
式中:a1、a2为回归系数;vu表示非机动车统一化后的速度,km/h;S表示非机动车统一化后的流量,由实际数据拟合得到,辆/(h·m)。
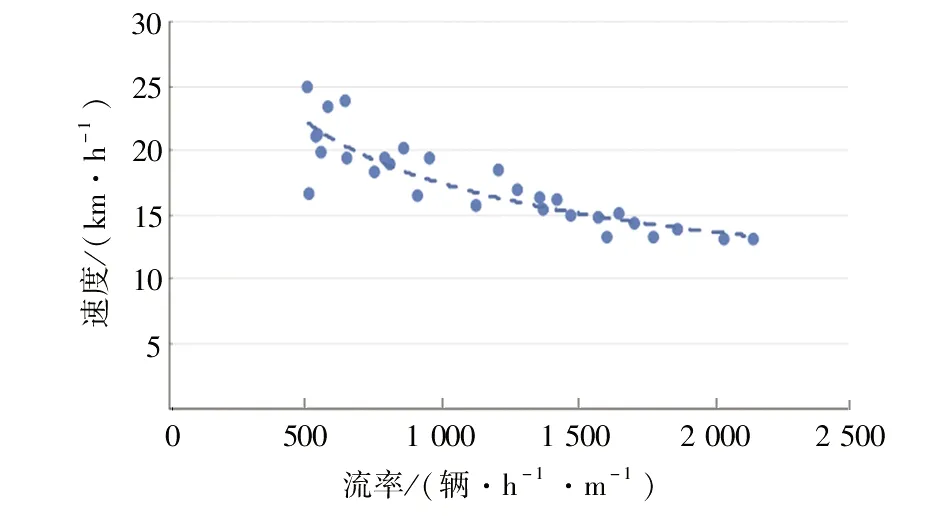
图4 速度-流量关系拟合图Fig.4 Fitting diagram of velocity-flow relationship
4.2 速度-流量模型的拟合检验
利用最小二乘法计算回归模型中的具体参数值,并对回归方程进行统计检验。模型摘要如表4所示,回归方程的显著性检验如表5所示,回归系数的显著性检验如表6所示,图5为标准化残差。
表5回归方程检验、表6回归系数检验(B值表示回归系数与截距)的显著性均为0.000,小于0.05,说明速度与流量之间存在相应关系且具有显著意义,图5回归标准残差曲线服从正态分布,能够较好地反映回归方程相应变量的变化规律;表4在未去除全部奇异值时,相关系数为0.868,判定系数R2为0.753>0.7,表明拟合效果较好。

表4 模型摘要Table 4 Model summary
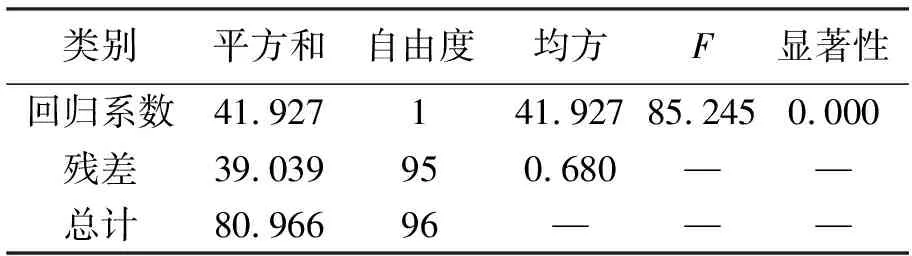
表5 回归方程的显著性检验Table 5 Significance test of regression coefficients
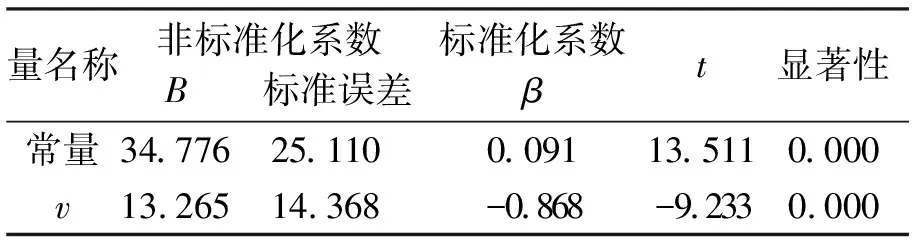
表6 模型回归系数分析Table 6 Model regression coefficient analysis
根据调查地点的速度-流量数据,得到回归方程为v=199.34S-0.352。
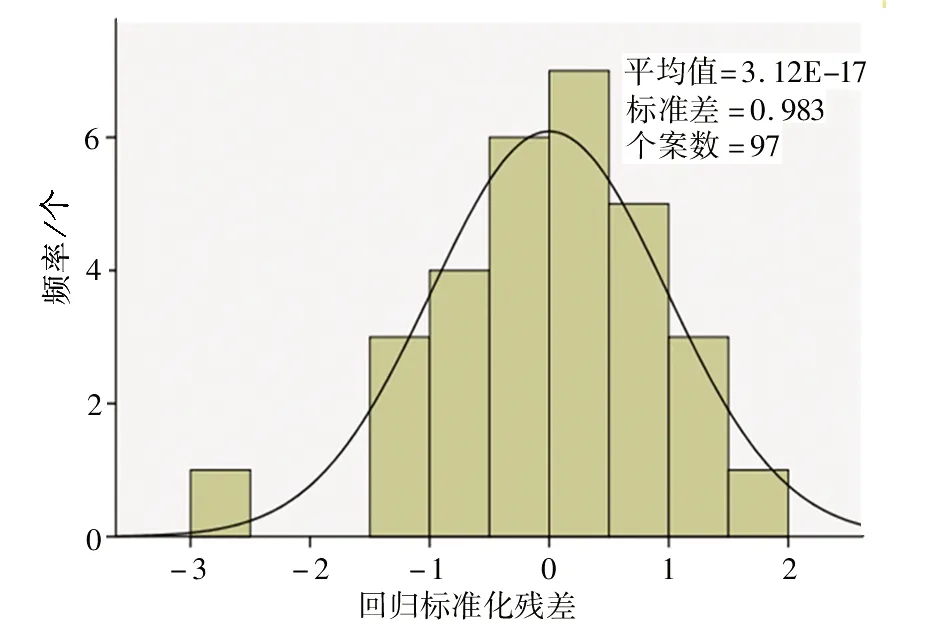
图5 回归方程标准化残差Fig.5 Standardized residuals of regression equations
5 结论
通过对非机动车交通流速度、流量的调查分析,发现其速度-流量之间具有明显的幂函数关系,回归方程为v=199.34S-0.352,R2为0.753﹥0.7,显著性<0.05,拟合效果较优。
