站在学生角度 突破思维障碍 解法自然

山东省淄博市周村区实验中学 王立功

几何证明问题，是学生感到困惑的问题类型之一。尤其是对于图形比较复杂的问题，学生常常出现思维障碍，找不到解决问题的方法。作为教师可以实现一题多解，学生一法难求。而当教师将方法讲给学生后，学生的收益往往甚微，再次遇到类似题目仍无法独立解决。教师没有达到“授之以渔”的目的。因此作为教师更应该站在学生的角度去思考和分析学生的思维障碍，引导和帮助学生从突破自身思维障碍出发，正确找出解决问题的方法。

下文笔者通过一个有代表性的一道几何问题，详细阐述如何从学生角度分析问题，解决思维障碍，最后得出多种解决问题的策略的思考过程，希望对读者有所帮助。

一、例题呈现

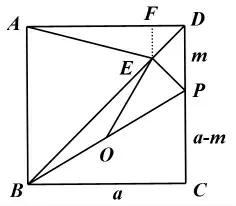
如图，在正方形ABCD中，点P是CD边上的动点，连接BP，点O为BP的中点，过点P作PE⊥BD，垂足为E。 连接EO，AE，猜想线段BP与AE之间的数量关系，并证明。

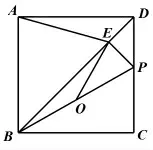
二、学生的思维障碍

1.题目的结论未知，仅通过直观观察看不出它们之间的数量关系；点P是一个动点，通过点P的运动，线段BP和AE都在变化，长度不是定值，学生感觉无从下手。

2. 题目中没有数据可以运用，BP和AE的长度无法求出。

3.BP和AE没有在同一个直角三角形中，所以通常三角函数等知识无法解决。

4.感觉BP和AE长度不相等，无法运用全等三角形解决。

三、站在学生角度，解决思维障碍，探索解决问题的方法

1.学生思维障碍一：结论未知，看不出两条线段是什么数量关系。

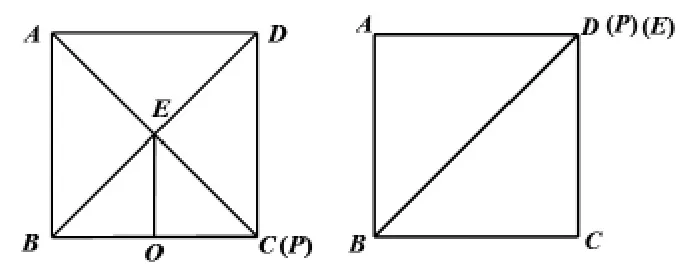
作为教师如果直接给出学生答案，或者直接利用证明的方式给学生讲解，最后得出结论对学生来说是收获甚微的。不利于学生思维的培养。因此教师可以站在学生的角度思考问题，如果看不出两者的数量关系可以从什么地方入手来思考。课堂上可以提问学生：“自己的困难在哪？”部分学生会回答：“看不出它们之间的数量关系。”教师顺势再问“为什么看不出来？”“因为点P是动点，长度不确定。”“那么你能感觉它们的关系是确定的吗？”“一定是确定的。”“那么与点P的位置有关吗？”“无关。”这时便有学生可以联想到未知问题的探索可以从猜测开始，而且对于动点问题可以通过特殊位置作出猜测，而特殊位置往往取运动的起始端和末端。当点P运动到点C时，点O运动到BC的中点处。点E恰好是正方形对角线AC与BD的交点，则容易算出；当点P运动到点D时，则点E恰好与D重合，此时容易算出故有不完全归纳法可以猜测出BP与AE的关系为BP=

2.学生思维障碍二：BP和AE长度不相等，无法运用全等三角形解决。

这种思维障碍是学生的思维狭窄，仅仅把线段关系理解为是否相等。因此教师应引导学生思考：两条线段除了在全等三角形中的相等关系，还会出现不等关系。即一条线段是另一条线段的倍数（或几分之几）。这样就可以引导学生思考如何解决不在一起的两条线段倍数问题。因此从学生思维的角度很容易得到可以证明两条线段所在的三角形相似，然后把目标线段之比转化成两条已知的线段之比。于是可以有下面的证明方法：

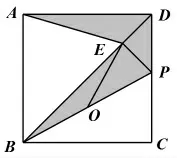
解后反思：构造三角形相似解决两条线段之比的问题是比较直接的方法。当然也可以通过过点A作AF⊥BD,垂足为点F，利用△AFE∽△BCP来解决。

3.学生思维障碍三：题目中没有数据可以运用，BP和AE的长度无法求出。

学生这种思维障碍限制在了仅仅运用数字来计算线段长度。为了突破思维障碍教师可以引导学生对于线段的计算除了有数字的代数计算外，还有代数式的运算。因此自然容易得到用设参数的方式表示出所求线段的长度。而对于两条线段的关系最一般的思路就是通过计算它们的长度进行比较，这样的解法更为自然。于是可以有下面的解法：

解法2：过点E作EF⊥AD，垂足为F.

设正方形的边长为a，DP的长为m，则PC=a-m，

在Rt△PBC中，根据勾股定理，

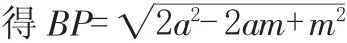
在等腰直角△DEP中，斜边DP=m，

当然对于线段的计算，教师可以进一步引导学生将图形放置在平面直角坐标系内解决。比如通过以点B为坐标原点，BC所在直线为x轴，以AB所在直线为y轴建立平面直角坐标系。再通过引入参数结合坐标系有关知识来解决类似问题。用代数知识解决几何问题，这也正是数形结合思想的重要体现。

4.学生思维障碍四：BP 和AE 不在同一个直角三角形中。

解决这个思维障碍就应引导学生思考是否可以想办法将两条线段放在同一个三角形中（即两条线段有公共顶点）。首先想到的便是将其中的一条（或两条）转化为与其相等的线段。最终借助第三方线段放在同一个三角形中。通过观察发现在正方形中AE=EC，而BP=2OE，故只要探索EC和OE的数量关系。因此容易想到连接OC，将上述问题转化到直角△EOC中。

解法3：连接OC，EC，由四边形ABCD是正方形，易证AE=CE，因为△BPE和△BCP都是直角三角形，又因为点O是BP的中点，所以BP，设∠EBP=α，则∠OBC=45°-α，∠EOP=α，则∠POC=90°-2α，故∠EOC=90°，由勾股定 理 得：OC2+OE2=EC2，所 以EC2=2OE2，即由BP=2OE，AE=EC，得

思路2：利用正方形对称性将AE转化为CE，问题就变成了BP如何转化到与EC有公共顶点的三角形中。故可以在点E或C处构造与BP相等的线段。因此利用E，B，C，P四点共圆，BP转化为EF。则由即可以解决。

解法4：连接CE，由四边形ABCD是正方形，易证AE=CE.因为PE⊥BD，所以∠PEB=90°，因为四边形ABCD是正方形，所以∠PCB=90°，所以点E，B，C，P四点在以点O为圆心，OE为半径的圆上，作出该圆，延长EO交⊙O于点F并连接CF，则BP，EF都是圆的直径，所以BP=EF，因为∠F=∠EBC=45°，所以△ECF是等腰直角

5.学生思维障碍五：部分同学可以探索出BP= AE，但思维障碍是如何构造： AE.

上述思维障碍产生的原因是学生对于直角三角形勾股定理以及三角函数知识点不够熟悉。教师应该引导学生思考，在什么情况下一个三角形中会出现倍的关系。因此学生很容易想到等腰直角三角形的斜边与直角边的比即为。因此可以利用旋转构造以AE为直角边的等腰直角三角形，得到然后将BP放在同一个三角形中。解决了这个思维障碍便可以得到如下解法：

解法5：将△ADE绕点A顺时针旋转90°，得到△AFB，连接EF，则△AED≌△AFB，得AE=AF，∠EAF=90°，FB=ED，∠ABF=∠ADE=45°，所以，因为PE⊥BD，∠EDP=45°，所以ED=PE，所以FB=PE，由∠ABD=45°，得∠ABF+∠ABD=90°，所以∠FBD=90°，所以FB∥PE，则四边形FBPE是平行四边形，所以BP=EF，因为

当然也可以将AE绕点A逆时针旋转90°，构造以AE为直角边的等腰直角三角形，得到

解后反思：直接告诉学生本题可以运用旋转变换来解决，对学生来说是有一定困难的。而通过解决学生思维障碍的角度看，构造等腰直角△FAE便会顺其自然。其本质也就是旋转。当然按照上述思路还可以先得到AE=EC，然后构造BP=

当然部分同学会想到AE=EC，仍然是存在思维障碍：如何构造因此可以类似上面解法，通过旋转构造以EC为直角边的等腰直角三角形。

四、反思

1.教师要放手让学生自己寻找解决思维障碍的方法。

传统的数学教学教师常常以自己为中心，不顾学生的实际情况，察觉不到学生的思维困难，而是任由教师按照自己的思路或知识逻辑灌输式教学。这也就导致教师讲解完例题之后学生真正掌握的非常少。学生没有把教师所讲的知识内化为自己的知识。所以当学生自己去解决问题时往往感到无所适从。学生遇到一个或多个思维障碍无法克服，长此以往便形成了学生思维的肤浅性和数学思维的消极性。因此教学中不能仅仅让优秀生完美地展示他们的过程，更应该鼓励解题有困难的同学暴露他们的思维障碍，通过解决思维障碍，引领他们思维的深度和广度，逐步培养学生的思维能力。前苏联教育家维果茨基曾提出儿童最近发展区理论。而学生思考问题的每一个思维障碍便是学生已有水平与将要解决的问题的差距。从学生思维的现有角度去思考和解决问题符合学生的发展规律。叶澜教授曾指出：“课堂教学中，教师应积极地看，积极地听，设身处地地感受学生的所作所为、所思所想，积极鼓励学生质疑问难，允许出错，允许改正”。教学中多鼓励学生多换一个角度想问题，勤问一下有困难的学生思考到了哪一步，你还需要哪些条件，你做了哪些尝试，等等。因此课堂教学中教师要站在学生的角度，教给学生克服思维障碍的方法才会让学生形成良好的解题习惯，真正提升学生的数学素养。

2. 解决思维障碍有助于实现一题多解，能够提炼通性通法。

几何证明题重在培养学生逻辑思维能力和分析问题的能力。一题多解就需要学生认真分析条件和结论，大致可以从哪几个大的方面去思考。每一条思路遇到思维障碍要及时变通，思考如何解决，遇到瓶颈更要学会有没有其他路线可以运用。打通每一个思路便是一种好的解题方法。当然教学中应当让学生去总结遇到类似的问题一般从哪些方面去解决，这就是通性通法。通性通法的总结和提升应当是学生在教师的引导下来总结，更多的是学生的思考，而不是教师的灌输。通性通法的总结有助于帮助学生解决学生思维障碍，实现高效解题。因此日常教学要教会学生通过解题反思自己的思维障碍，并以此总结通性通法。

3.以生为本，尊重学生的认知规律，课堂教学积极应对学生的思维障碍。

教学中教师要想了解到学生的思维障碍就应从学生的学习实际出发，了解到每一名学生存在的思维障碍。比如小组合作尽量不要让优秀的同学讲解自己独到的方法，让他们成为一言堂。而更应该利用学习小组鼓励思维有困难的同学先讲解自己的思路，暴露自己的思维障碍，然后由同学或老师帮助解决。这样的合作才更有效。组长对本组内每一名学生的思维障碍反馈给教师，教师根据学情有针对性的讲解，打通每一名同学的思维障碍，这才是真正的以学定教，这样的课堂才更有实效性。

4.鼓励学生有克服困难的信心。

对于几何问题的教学，应鼓励学生敢于应对困难，提升自己思维的敏捷性。遇到思维障碍导致思路停滞不前时，善于寻找突破思维障碍的关键因素。对题目的已知条件和隐含条件重新梳理，对自己的思考方向寻找突破口。鼓励学生善于变换角度思考问题，拓宽自己的思维视角。当然对于一个几何问题的解决不一定有多种证明方法，但是当学生具备了能够突破自己思维障碍的思维品质时，自己的解题能力会有较大提升。对于教师的教学来说，应该做到以生为本，真正落实学生的主体地位。教学中将自己的思维“放低”，站在学生的立场思考问题，和学生一起思考解决问题的方法。善于运用“台阶式”的问题启发学生的思维，逐步克服学生的思维障碍，实现高效的数学课堂。