巧用几何画板 探究存在问题*——以“二次函数背景下直角三角形存在性问题”为例

广东省中山市东区松苑中学(528400) 张青

存在性问题是命题的结论不确定的一类问题,常以“是否有”、“是否存在”、“是否变化”等词语出现,是中考数学的常见题型,直角三角形的存在性问题常与二次函数、一次函数有机结合起来考察,对知识的迁移能力、分析问题和灵活运用问题的能力要求较高,发现和总结二次函数背景下直角三角形存在性问题的解题方法,对于夯实“四基”,发展“四能”,培养学生的理性思维意义重大,在问题解决的过程中,通过“学会”走向“会学”.

1 内容分析

1.1 地位和作用

函数是初中数学的核心内容,以二次函数为载体的直角三角形存在性问题,是中考的重点也是难点,综合考察了学生的运算能力、逻辑推理能力、数学抽象能力等,借助几何画板的动态直观演示,通过本节课的教学设计,帮助学生整体复习二次函数的性质、一次函数的性质、勾股定理、直角坐标系等相关知识,帮助学生建立二次函数、一次函数、三角形、直角坐标系之间的联系,构建更广阔、更简约的知识体系,促进学生思维发展.

1.2 思想方法

数形结合、分类讨论、转化

1.3 能力发展

基于二次函数背景下的直角三角形存在性问题,建立二次函数与三角形、一次函数的联系,在寻找问题解决的过程中,发展了学生的数学抽象能力,培养了学生的逻辑推理能力和直观想象能力.

1.4 教学重点

学会从代数和几何两方面寻找基于二次函数背景下直角三角形存在性问题的解决方法,并且解决新的问题.

2 教学目标

(1)回顾二次函数和直角三角形的相关性质,会用待定系数法求函数的解析式.

(2)掌握“以二次函数为载体的直角三角形存在性问题”的代数方法和几何方法,领悟分类讨论的数学思想方法.

(3)结合图像理解二次函数、一次函数、三角形之间的关系,感受数形结合、转化的数学思想.

(4)能根据具体问题选择合适的数学方法,发展逻辑推理和直观想象能力.

3 教学问题诊断分析

3.1 学生已有的基础

学生已经复习了二次函数、一次函数的图像和性质、勾股定理等相关知识,初步理解了数学知识的相关联系,知道了分类讨论、转化、数形结合等数学思想.

3.2 存在的困难

学生面对分类讨论的问题有“畏难心理”,很难建立函数与直角三角形之间的联系,难以合适构建“数学模型”,从而解决数学问题.

3.3 教学难点

学生难以借助“数形结合”研究数学问题,尤其是当动点在二次函数图像上时,在解决综合问题上有困难.

4 教学过程

4.1 知识回顾,方法渗透

例1 如图1,已知抛物线y=-x2+bx+c与直线AB相交于A(-3,0),B(0,3)两点.

图1

(1)求抛物线的解析式;

(2)设C是抛物线对称轴上的一动点,求使∠CBA=90°的点C的坐标.

解析:(1)把点A(-3,0),B(0,3)代入y=-x2+bx+c易得y=-x2-2x+3.

(2) 法一(如 图2) :过点B作CB⊥AB,交抛物线的对称轴于点C,过点C作CE⊥y轴,垂足为点E,∵y=-x2-2x+3,∴抛物线对称轴为直线x=-1,∴CE=1,∵AO=BO=3,∴∠ABO=45°,∠CBE=45°,∴BE=CE=1,∴OE=OB+BE=4,∴点C的坐标为(-1,4).

图2

法二(如图3) :设C(-1,m),∵∠CBA=90°,根据勾股定理得AB2+BC2=AC2,即32+32+12+(3-m)2=22+m2,解得m=4.∴点C的坐标为(-1,4).

图3

法三:设C(-1,m),∵∠CBA=90°,∴kBC ·kAB=-1,即=-1,解得m=4.∴点C的坐标为(-1,4).

【设计意图】通过本题的学习回顾用待定系数法求解二次函数的解析式,初步体会直角三角形的性质,运用勾股定理相关知识表示直角三角形的三边关系,体会“数形结合”的数学思想方法,初步体会方法的多样性,感受“数形结合”方法的“简洁性”.

【信息技术运用】通过几何画板现场直观展示动点所在位置,以几何画板为载体,通过“图文并茂和标注颜色”直观感受,搭建“数”与“形”的桥梁,当∠CBA=90°时,求得点C的坐标.

4.2 知识运用,分类讨论

例2 (2020 年内蒙古通辽市中考试卷改编)如图4,在平面直角坐标系中,抛物线y=-x2+bx+c与x轴交于点A、B,与y轴交于点C.且直线y=x-6 过点B,与y轴交于点D,点C与点D关于x轴对称,过点P(2,0)作x轴的垂线交抛物线于点M,交直线BD于点N.

图4

(1)求抛物线的函数解析式;

(2)在y轴上是否存在点Q,使得以Q,M,N三点为顶点的三角形是直角三角形? 若存在,直接写出点Q的坐标;若不存在,说明理由.

解析:(1)抛物线的解析式为:y=-x2+5x+6(略).

(2)把x=2 代入y=-x2+5x+6得M(2,12),把x=2 代入y=x-6得N(2,-4).

当∠QMN=90°时(如图5),QM//x轴,则Q1(0,12);

图5

当∠MNQ=90°时(如图6),NQ//x轴,则Q2(0,-4);

图6

当∠MQN=90°时,设Q(0,n).

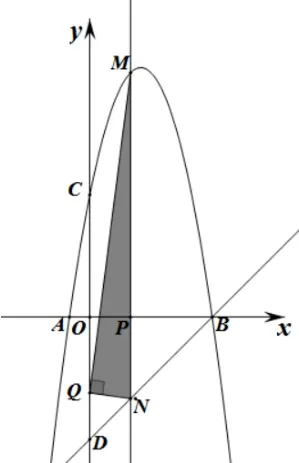
图7

图8

【设计意图】当动点P在一条直线上时,探索不同解决问题的办法,感受代数和几何方法的异同,掌握函数背景下直角三角形存在性问题的解决方法,领悟“转化”、“分类讨论”和“数形结合”的数学思想方法,建立二次函数、一次函数、三角形之间的联系,构建知识体系.

【信息技术运用】通过几何画板,搭建“数”与“形”的桥梁,通过图形直观,感受数学思想,将复杂的数学问题清晰可视化,从而达到解决问题的目的.

4.3 知识升华,拓展运用

变式练习:如图9,在平面直角坐标系中,抛物线y=ax2+2x+c与x轴交于A(-1,0),B(3,0)两点,与y轴交于点C.

图9

(1) 求抛物线的解析式和直线AC的解析式;

(2)试探究:在拋物线上是否存在点P,使以点A,P,C为顶点,AC为直角边的三角形是直角三角形? 若存在,请求出符合条件的点P的坐标;若不存在,请说明理由.

解析:(1)二次函数的解析式为y=-x2+2x+3,直线AC的解析式为y=3x+3.(略)

(2)解:设P(m,-m2+2m+3),当PC⊥AC时(如图10),过C点作直线l垂直于y轴,过点A、P分别作直线垂直于直线l,并且与直线l分别交于点D、E,垂足分别为点D、E.

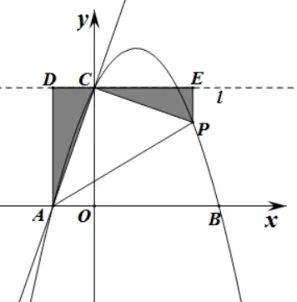
图10

图11

【设计意图】当动点P在抛物线上时,通过分析问题,发现利用勾股定理表示三边关系会出现四次方,计算比较繁琐,寻找其他方法,巧用“数形结合”,利用三角形相似或者三角函数可以解决问题,感受“数形结合”方法的“间接性”,通过“学会”转向“会学”,进一步领悟“分类讨论”、“转化”、“数形结合”等思想方法.

【信息技术运用】借助几何画板,感受“数形结合”思想方法的优越性,培养学生的直观想象能力,发展学生的逻辑推理能力,促进深度教学.

4.4 归纳小结,构建体系

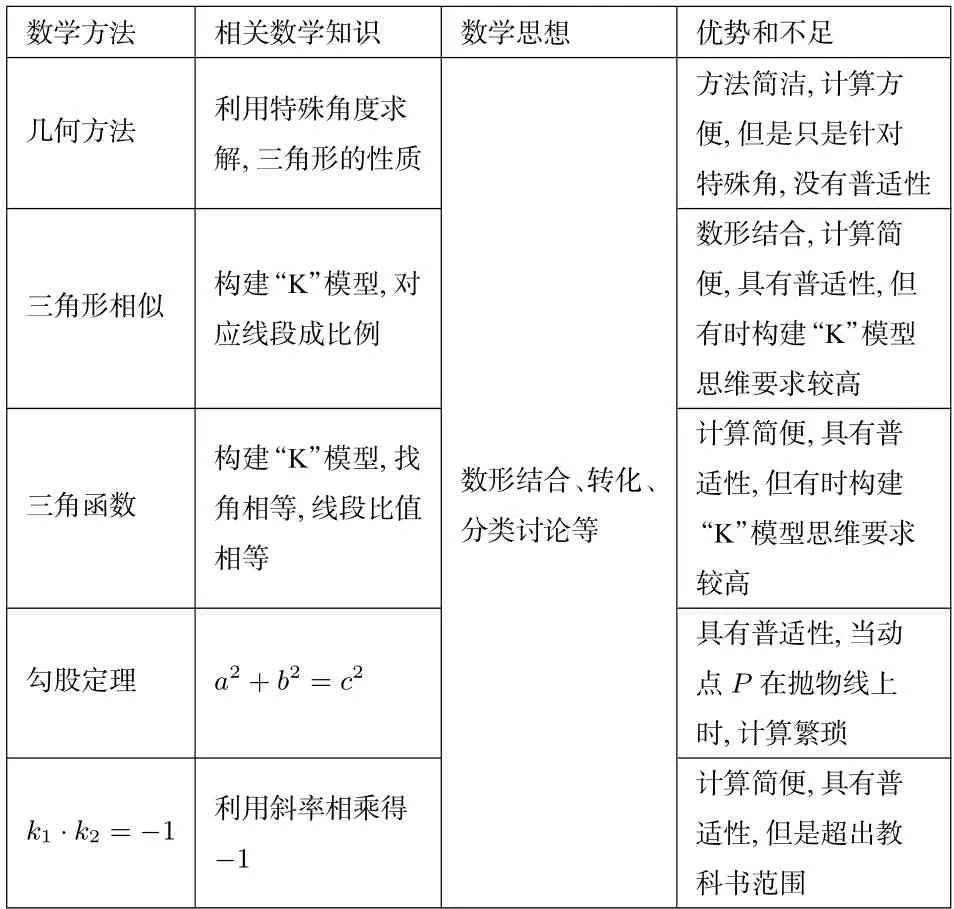
5 教学思考

5.1 以几何画板为催化剂,助推一题多解

《义务教育数学课程标准(2011 年版)》指出:“经历从不同角度寻求分析问题和解决问题的方法的过程,体验解决问题方法的多样性,掌握分析问题和解决问题的一些基本方法[1].”让学生通过小组合作学习,借助几何画板的动态演示,让学生直观感受二次函数背景下直角三角形存在性问题的过程,假设直角三角形存在,根据已知条件建立等量关系,得出正确结论,如果得出的结论与题意矛盾,则不存在,在解决问题的过程中发展了学生逻辑推理能力,在运用“数形结合”思想建立数学模型的过程中,发展了学生直观想象能力,在运用勾股定理等数学知识解决问题的过程中发展学生的数学运算能力,教师在教学过程中鼓励学生根据题意选择适合的数学方法,让“核心素养”在课堂的主阵地上落地生根.

5.2 以几何画板为载体,渗透数学思想

“存在性问题”综合考察了学生的运算能力、逻辑推理能力、数学抽象能力、直观想象能力等,对学生的思维要求较高,直观想象是抽象思维的基础,教师在教学过程中以几何画板为载体,通过图形直观,将点线之间的关系显性化,将复杂的数学问题进行分解,通过“数”与“形”的结合,把抽象的数学问题、不好理解的数学知识变得直观、可理解,使问题解决的思路有序化、可视化、清晰化,体现数学“简约美”,渗透转化、分类讨论、数形结合等数学思想方法,引领学生深度思考.

5.3 以几何画板为桥梁,通过“学会”走向“会学”

郑毓信教授在“数学深度教学”十讲中提到数学教育的目标由“帮助学生学会数学地思维”转向“通过数学学会思维[2].”“深度教学”是从思维激发角度达到“深度”,利用几何画板辅助初中课堂教学,搭建“数”与“形”的桥梁,激发学生的“思维”,通过“二次函数背景下直角三角形存在性问题”专题复习的数学思想方法拓展到等腰三角形、等边三角形、平行四边形存在性问题,从“学会”转向“会学”,引领学生深度思考,让学生真正成为学习的“主人”.