基于芳纶平纹织物微观几何结构的纱线抽拔力学性能分析
2022-04-24刘岳岩胡瀚杰
马 莹, 刘岳岩, 赵 洋,2, 陈 翔, 禄 盛,2, 胡瀚杰
(1. 重庆邮电大学 先进制造工程学院, 重庆 400065; 2. 西安交通大学 机械结构强度与振动国家重点实验室, 陕西 西安 710049; 3. 重庆交通大学绿色航空技术研究院, 重庆 401120)
芳纶平纹织物具有高比强度、绝热阻燃和应力分布均匀等特点,是抵抗弹道冲击的优质材料[1]。然而,由于纱线空间构型的复杂多样性和冲击加载所带来的高瞬态、高度非线性等问题,为该研究带来巨大挑战。
现有研究多通过实验来探索织物尺寸、材料属性和初始条件对纱线抽拔的影响规律。Kirkwood等[2-3]、Nilakantan等[4]、Zhu等[5]和Bai等[6]都探究了织物尺寸和横向预紧力对芳纶平纹织物抽拔性能的影响规律。Dong等[7]设计了多种芳纶织物单纱抽拔与弹丸冲击对比实验,提出包含纤维直径和纤维模量的纱线抽拔力计算公式。Bilisik等[8-12]设计了不同密度的芳纶织物纱线抽拔实验。上述研究方法均能有效展示各因素对纱线抽拔性能的影响规律,但未能揭示抽拔过程中的应力传播和能量转换机制。Dong等[7]使用ABAQUS模拟了平纹织物的纱线抽拔过程,该模型将被抽拔的纱线模拟为高度简化的多层长条,将其余纱线模拟为刚体。Valizadeh等[13]采用单胞函数模型和整体仿真2种方法,在ABAQUS中模拟了平纹织物的纱线抽拔过程,该模型中被抽拔的纱线为实体单元,其余纱线由壳体单元组成。朱德举等[5]建立了由实体单元组成的平纹织物模型,并使用LS-DYNA模拟其抽拔过程。以上研究方法所用织物模型均较为理想化,忽略了纱线截面形状变化,且未能有效解决纤维力学属性对抽拔性能的影响。
织物由丝束编织而成,每根丝束由单根或多根纱线构成,而每根纱线含有数百根纤维,因此,织物几何结构可以在丝束、纱线和纤维尺度上进行分析构造。在微观尺度上,纱线的空间构型由纱线中每根纤维的路径决定。亚纱线尺度的织物几何结构建模方法,弥补了纱线尺度建模方法在探索织物微观几何结构、尺度间的能量转化和纱线真实空间构型等问题上的局限性,进而促进织物的力学性能和损伤机制研究。Nilakantan[14]和文献[15-17]均建立了单根纱线的微观几何模型,并使用有限元软件进行受力分析。虽然上述2类纱线模型中纤维数量趋近于真实纤维数量,但截面形状和纤维间的排列方式较为理想化,与真实纱线内部结构存在差距,无法比拟真实纱线受力时的动力学响应。
本文参考文献[2-3]和[5,18-20]等抽拔实验方案设计实验,以获得芳纶平纹织物抽拔力-位移曲线;进而基于数字单元法理论[21-23],构建可反映织造工艺及纤维间相互作用的芳纶平纹织物变截面几何模型,在ABAQUS中进行纱线抽拔过程仿真,并与实验结果进行对比验证分析。该研究旨在获得纱线抽拔过程中织物内部的能量转换机制,横向预紧力和纱线间的摩擦因数对抽拔力的影响规律,为织物几何结构设计和力学性能预测提供方法和依据。
1 实验部分
图1(a)示出纱线抽拔实验示意图。实验装置由织物固定装置和抽拔装置构成,织物固定装置主要由外侧钢架、两侧夹具、传动螺杆及预紧力传感器构成。

图1 纱线抽拔装置及过程示意图Fig.1 Schematic diagram of yarn pull-out device(a) and process (b)
沿水平方向将芳纶织物纬纱左侧置入固定夹具,织物纬纱右侧置入滑动夹具中,实验前保持2个夹具间纬纱宽度为15 mm。可旋转螺杆上的螺母带动右侧夹具沿轴承水平滑动,通过改变夹具间距对织物施加不同的横向预紧力,并经传感器测得预紧力大小。抽拔装置由珠海市三思泰捷电器设备有限公司生产的气动夹具、力值传感器及CMT-5105电子万能试验机连接杆构成,沿竖直方向使用气动夹具夹紧单根经纱,并将传感器连接到试验机来测量抽拔力的大小。
纱线抽拔主要分为2个阶段:静摩擦阶段和动摩擦阶段,如图1(b)所示。在静摩擦阶段,被抽拔纱线的末端位置保持不变,受力端沿抽拔方向移动,纱线由屈曲状态缓慢伸直,该阶段抽拔力与纱线受力端位移几乎呈线性关系。当抽拔力达到峰值纱线呈伸直状态,此时进入动摩擦阶段,整根纱线沿抽拔方向平移,抽拔力呈正弦曲线式下降波动。每当被抽拔纱线的末端滑入和滑出一个经纬纱线的交叉点时,抽拔力达到最大和最小。
2 理论模型
在本文模型中,将被抽拔纱线以外的织物部分视为连续体矩阵。纱线抽拔过程中,被抽拔纱线与织物一直处于静态平衡,可得
(1)
式中:F为被抽拔纱线所受的张力大小,N;x为被抽拔纱线的长度,m;ψ为纱线的等效面积,m2;τ为经纬纱线交叉点处的剪应力,Pa。当F较小时,τ与被抽拔纱线受力端移动距离S呈线性关系。纱线移动距离可通过纱线伸长量与连续体矩阵的缩短量之差来定义

(2)

(3)

(4)
式中:L为纱线长度,m;Fpull=F(L),即x=L时的抽拔力,N。分别对式(1) 和式(4)求导并联立可得
(5)
将式(4)除以式(5)可得到静摩擦下F与τ的函数关系为:
(6)
在静摩擦阶段随着抽拔力的增加,已经伸直的纱线长度为d,仍处于屈曲状态的纱线长度为L-d。抽拔力F1可表示为纱线从屈曲到伸直所需抵抗的阻力Fst和已经伸直的纱线滑移出织物所需抵抗的阻力Fsl:
(7)
式中:τmax为静摩擦阶段最大剪应力,Pa;τconst为动摩擦阶段最大剪应力,Pa。将边界条件F(0)=0、F(L-d)=Fst,代入式(4)可得:
(8)
F(x)=Fst+τconstψ(x-L+d),L-d≤x≤L
(9)
在动摩擦阶段纱线已完全伸直,抽拔力可表示为
F(x)=τconstψx, 0≤x≤L-Δd
(10)
式中,Δd为纱线末端的移动距离,m。
3 数值模型
本文研究所用芳纶织物面密度为220 g/m2,厚度为0.3 mm,单胞长和宽分别为2.997[5,24]和2.982 mm[25], 在索维特特殊线带有限公司织造而成。每根纱线约包含1 000根纤维,纤维体密度(Di)为 1.44 g/cm3, 弹性模量(E11)为110 GPa,线密度为 165.6 tex, 直径为12 μm,购自美国杜邦公司。
3.1 平纹织物几何模型
3.1.1 微观模型
织物结构的最小重复单元为单胞,为大幅提高计算效率,可忽略单胞间的细微差异,采取仅对单胞进行建模,然后在经纬方向拼接的方法得到织物模型。图2示出平纹织物纤维离散过程。根据平纹织物的单胞结构建立初始松弛模型,此时经、纬纱线各由1根数字纱线组成,其截面形状为圆形。由于在真实织造过程中,纱线截面形状随时间发生变化,为模拟这一特征,分5次对纱线进行纤维离散化处理,通过在经、纬纱线首尾两端施加0.2 N张力,使纤维在张力的作用下发生相对运动,改变纱线截面形状直至织物整体势能变化趋近于0。仿真过程中经纬方向的数字纤维首尾2点始终保持在同一水平高度,在长度或宽度方向上相距1个单胞长度,实现织物结构的周期性。织造过程历时84.315 ms,随着纱线中纤维化离散程度的增加,纤维体积分数增加,织物厚度减小,其几何结构趋近于真实织物。当经纬纱离散为112根数字纤维时,所得平纹织物面密度为223 g/m2,厚度为0.342 mm,与真实织物仅分别相差1.34%和14%。

图2 平纹织物纤维离散过程Fig.2 Discrete process of plain weave fabric
3.1.2 细观模型
由于纱线抽拔过程中不涉及纤维断裂等失效情况,为使织物模型的尺寸接近真实织物大小,而避免在仿真过程中耗费大量内存,本文基于微观尺度的织物几何模型计算得出真实纱线轮廓形状,进而使用变截面细观尺度织物模型模拟纱线抽拔。
纱线轮廓的计算涉及的参数有:d为2个纱线轮廓线的间距,m;R为与纱线横截面面积大小相等的圆的等效半径,m;Rs为用于确定纱线轮廓曲线的圆辊半径,m;r为数字纤维半径,m;n为纱线轮廓等分直线的数量。其中d/R=0.5,Rs/r=15,n=48。

图5 织物表面结构和纱线截面对比图Fig.5 Comparison of fabric surface and yarn cross-section shape. (a) Actual fabric surface; (b) Numerical fabric model surface; (c) Comparison between actual and numerical yarn cross-section shape
以图2所示单胞起始位置处纱线截面为例,该纱线轮廓计算方法分为以下3个步骤。首先,通过组成数字纤维的节点和杆单元所在位置和方向计算纱线路径,该路径经过纱线截面几何中心,并与所在截面垂直。其次,在垂直于纱线路径的平面,沿纱线横截面逆时针滚动半径为Rs的圆辊,获得由圆辊圆心轨迹形成的闭合曲线,如图3(a)所示。最后,将圆辊沿闭合曲线内侧逆时针滚动,获得由圆辊圆心轨迹形成的新的闭合曲线,如图3(b)所示。将该曲线等分为n份,用直线依次连接起来,即为纱线横截面的轮廓。

图3 纱线截面轮廓计算示意图Fig.3 Calculating schematic diagram of yarn cross-section profile. (a) Outer yarn profile;(b) Inner yarn profile
每间隔距离d的长度重复以上3个步骤,重新计算一次纱线横截面轮廓,并用直线将2个相邻的纱线截面轮廓在等分处连接,形成纱线表面网格。圆辊半径Rs和纱线轮廓等分直线的数量d影响纱线截面轮廓的真实程度,轮廓线间距n影响纱线表面的真实程度。圆辊半径和轮廓线间距越小,纱线轮廓等分直线的数量n越大,所得纱线几何结构越趋近于真实纱线,反之则越趋近于理想模型,纱线表面网格示意图如图4所示。用此方法可获得变纱线截面形状的真实织物细观几何模型,其与实际纱线截面和织物表面对比[13]如图5所示。

图4 纱线表面网格计算示意图Fig.4 Schematic diagram of calculating yarn surface mesh
3.2 纱线抽拔模型
3.2.1 材料属性
由线密度与体密度的比值可得到理想化的纤维束横截面积Ai为0.115 mm2,但纤维间排列存在间隙,纱线与纤维材料参数未形成线性关系,需要通过理想纤维束与纱线横截面关系获得真实纱线的弹性材料参数。通过CATIA软件测得所建纱线模型的平均面积Ar为0.150 8 mm2,则纱线密度Dr可表示为
(11)
式中,Di为纤维体密度,g/m3。纱线的轴向弹性模量E11可表示为
(12)
由Gasser等[26]研究可知,当G12、G13、G23与ν12、ν13、ν23较小,且E22和E33为E11的十分之一时,则模型具备正交异性线弹性纱线行为,具体参数如表1所示。其中:G12、G13、G23为对应方向的剪切模量;ν12、ν13、ν23为对应方向的泊松比;E22、E33、E11为对应方向的弹性模量;下标数字1、2、3代表坐标系,设置纱线为正交各向异性材料,其中1为纱线路径的切线方向,与纱线截面轮廓垂直;2为纱线截面与形心相距最远的方向;3为材料方向1和方向2的叉乘。

表1 纱线正交异性线弹性材料参数Tab.1 Parameters of yarn orthotropic linear elastic material
3.2.2 网格划分准则
平纹织物纱线抽拔过程受力方向均位于同一平面,纱线弯矩对抽拔行为影响较小,可忽略不计。在厚度方向只布种1个减缩积分实体单元来降低纱线弯曲刚度,准确表征其高挠曲柔韧特性如图6(a)所示。
图6 网格划分示意图Fig.6 Schematic diagram of mesh division. (a) Mesh unit division; (b) Meshed yarn cross-sectional shape with local seed distribution
本文采用六面体为主的网格划分方法,经纱节点密度为0.1,纬纱节点密度为0.08。将纱线从中间平面等分为2个部分,将中间平面向左右各移动0.6 mm建立2个基准面,并对端面进行局部布种,保证端面各节点间单元数为1,最终可得每根纱线的网格单元数量约为2 350个,如图6(b)所示。
3.2.3 初始条件
在纱线间建立通用接触,耦合织物上下端面,令摩擦因数为0.2,抽拔速度为1.67 mm/s。抽拔仿真通过以下2个分析步进行模拟:首先固定纬纱下端面,并对上端面施加横向预紧力,在10 s内将横向预紧力从零线性增加到设定值,并在5 s内保持不变;其次固定纬纱的上端面,并沿经纱方向匀速抽出指定纱线。
4 结果与分析
4.1 能量转化机制
图7示出预紧力为100 N,尺寸为50 mm×14.91 mm的织物受到纱线抽拔时能量随时间变化曲线。

图7 能量-时间曲线Fig.7 Energy-time curves
由图7可知,整个纱线抽拔过程中外力做功主要转化为应变能、摩擦耗能和动能,其中动能趋近于零而远小于应变能与摩擦耗能。在0~15 s施加横向预紧力阶段,织物主要通过应变能吸收能量;随着横向预紧力的线性增大,纱线的应变能也线性增大,当时间为10 s时预紧力达到设定值,应变能逐渐趋于平衡,应变能占此阶段外力做功的72.10%;在 15~45 s 纱线抽拔阶段,外力做功主要通过摩擦耗能来吸收能量,摩擦耗能占此阶段外力做功的85.83%;随着抽拔的进行,4条曲线逐渐趋于平衡。
4.2 纱线抽拔力
图8示出预紧力为100 N,尺寸为50 mm×14.91 mm的织物受到的纱线抽拔力随时间变化曲线。可以看出,仿真所得抽拔力线性增大到峰值后呈正弦衰减,波动频率与实验一致,抽拔力峰值与实验相差5.96%。对比整个仿真与实验抽拔过程中产生的抽拔力峰值和每个波峰、波谷,其平均差值依次为0.27、0.42和0.05 N。可得该仿真模型能够较为有效地预测纱线在各位移时的抽拔力,其中对波谷的预测最为接近。

图8 仿真和实验抽拔力-位移曲线Fig.8 Simulation and experimental pull-out force-displacement curves
图9示出预紧力为100 N,尺寸为50 mm×14.91 mm的织物受到的纱线预紧力与位移变化曲线。
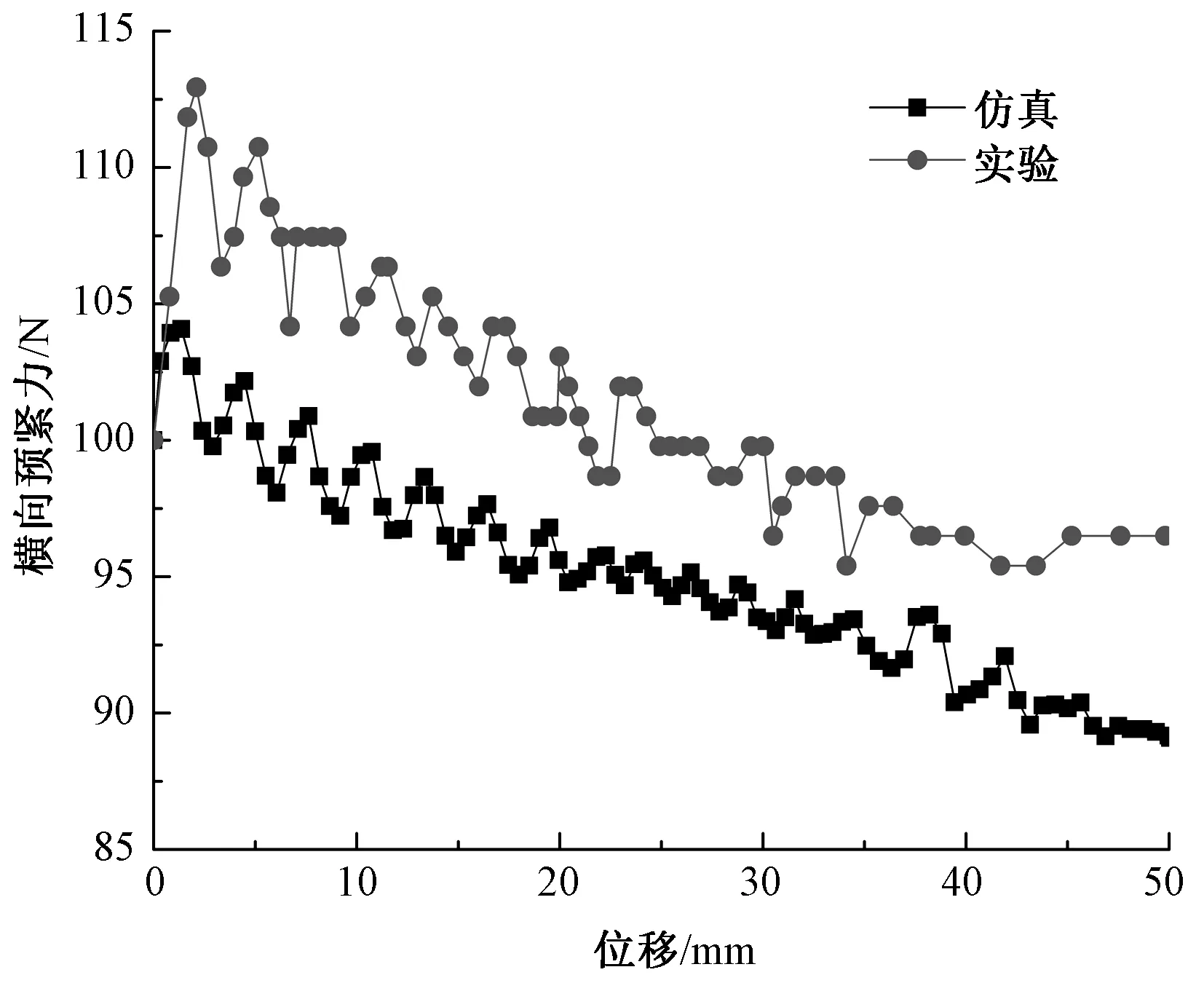
图9 仿真和实验预紧力-位移曲线Fig.9 Simulation and experimental pre-tension force-displacement curves
由图9可知,仿真所得横向预紧力波动情况和抽拔力相似,横向预紧力峰值为104.08 N,与实验值仅相差-8.51%。由于横向预紧力大小受纱线弯曲刚度的影响,受限于织物模型的尺度,只能通过网格划分的方法降低纱线的弯曲刚度,以达到准确表征纱线柔韧特性的目的,所以横向预紧力整体大小略小于实验值。以上结果验证了该模型的有效性。
4.3 参数化分析
本文取尺寸为15 mm×14.91 mm的织物模型,研究横向预紧力和摩擦因数对抽拔力峰值和衰减速度的影响规律。
4.3.1 横向预紧力
图10示出横向预紧力对抽拔力的影响。可知,横向预紧力为0、100、200和300 N时,随着横向预紧力增加,抽拔力峰值也不断增大。当横向预紧力为0 N时,经纱每通过1根纬纱,抽拔力衰减为0 N。由图10(b)可知:当横向预紧力从0 N增加至100 N时,抽拔力峰值增大383.16%;当横向预紧力从 100 N 增加至200 N时,抽拔力峰值增大了36.25%;当横向预紧力从200 N增加至300 N时,抽拔力峰值增大21.51%。表明随着横向预紧力不断增大,其对纱线抽拔力增加的影响程度逐渐减小。

图10 横向预紧力对抽拔力的影响Fig.10 Effect of transverse pre-tension on pull-out force. (a) Pull-out mechanical and displacement curve;(b) Linear fitting of peak pull-out force curve
4.3.2 摩擦因数
经纬纱线的摩擦因数计算公式为:
μ=μd+(μs-μd)e-ξ|Vrel|
(15)
式中:Vrel为纱线表面相对运动速度,m/s;μd为动摩擦因数;μs为静摩擦因数;ξ为指数衰减因数。忽略抽拔速度对摩擦因数的影响,令ξ为0,得到μ=μs。
将各横向预紧力下的摩擦因数(y)变化对抽拔力峰值(x)的影响拟合为线性方程y=kx+b,研究了3种不同横向预紧力作用下,纱线间摩擦因数变化对抽拔力的影响如表2所示。可知,随着纱线间摩擦因数的减小,k和b也随之减小。
图11示出摩擦因数对纱线抽拔力的影响。可知,当预紧力为100、200和300 N时,摩擦因数与抽拔力成正比,随着摩擦因数的减小,抽拔力峰值也依次减小。当摩擦因数从0.20降低至0.15时,抽拔力峰值平均下降26.26%;当摩擦因数从0.15降低至0.10时,抽拔力峰值平均下降29.07%。表明随着纱线间摩擦因数的减小,抽拔力峰值减小速度逐渐变快。
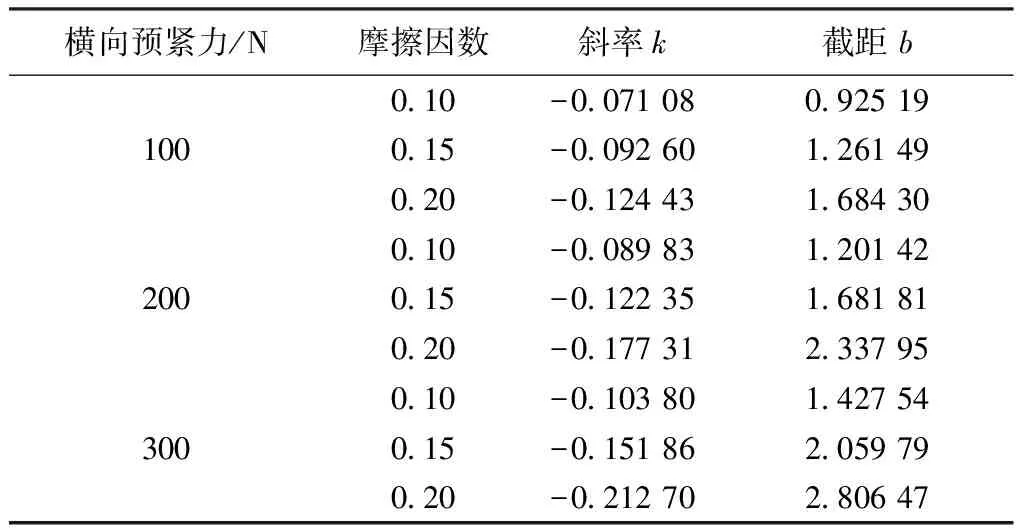
表2 各摩擦因数下的峰值线性拟合Tab.2 Linear fitting of peak values under various friction coefficients

图11 摩擦因数对纱线抽拔力的影响Fig.11 Effect of friction coefficient on yarn pull-out force
5 结 论
本文从纤维尺度模拟了芳纶平纹织物的织造过程,并对其内部微观几何结构进行预测与建模;然后根据该微观模型计算出真实的纱线空间构型,并导入ABAQUS进行抽拔仿真和实验对比分析。在此基础上获得了横向预紧力和纱线间摩擦对抽拔性能的影响,得到如下主要结论。
1) 数字单元法所建平纹织物几何模型中,纱线表面和截面形状与真实织物一致,能够反应其微观几何结构特征。
2) 抽拔过程中,在施加横向预紧力阶段,应变能吸收外力做功占72.10%;在纱线抽拔阶段,摩擦耗能吸收外力做功占85.83%,随着抽拔的进行,外力做功、摩擦耗能、动能和应变能趋于平衡。
3) 对于50 mm×14.91 mm大小的织物,仿真所得抽拔力峰值、抽拔力波峰和波谷与实验值平均差值分别为0.27、0.42和0.05 N,所得横向预紧力峰值与实验值仅相差-8.51%,证实了方法的有效性。
4) 对于15 mm×14.91 mm大小的织物,随着横向预紧力的增加,抽拔力峰值的增加程度逐渐减缓;随着纱线间摩擦因数的减小,抽拔力-位移曲线峰值线性拟合的斜率绝对值与截距也随之减小。
