跨厚比对高强玻璃纤维增强复合材料单向板弯曲性能的影响

白 鑫, 王云英, 王雅娜, 陈新文, 何玉怀

（1．中国航发北京航空材料研究院, 北京 100095；2．南昌航空大学 材料科学与工程学院, 南昌 330063）

玻璃纤维/聚合物基复合材料具有高比强度、高比模量、优异的耐疲劳性能、良好的耐腐蚀性能且价格较低等优点，广泛应用于航空航天、汽车工业、体育器械等领域[1-5]。大多数材料或构件在使用过程中不可避免地会受到弯曲载荷作用而产生损伤或破坏，所以复合材料的弯曲性能（弯曲强度、弯曲模量等）是质量控制、应用评价必须考虑的关键性能指标。弯曲性能测试方法主要有三点弯曲、四点弯曲测试法，其测试结果都会受到层间剪切应力的影响。研究表明，跨厚比的变化能改变层间剪切应力对弯曲性能测试的影响[6]。国内外相关标准对跨厚比的规定均不相同，国内外研究者对此进行了一些相关研究[7-8]。

周少荣等[9]研究了跨厚比对C/C 复合材料层合板室温、高温弯曲性能测试结果的影响，结果表明，当跨厚比大于临界跨厚比时，C/C 复合材料的弯曲强度不再增加，层间剪切应力对弯曲性能的影响随跨厚比的增加逐渐削弱。Syayuthia 等[10]研究了不同跨厚比（32、40、60）的碳纤维/环氧树脂复合材料夹层板三点弯曲测试结果的影响，结果表明，当跨厚比增大时，碳纤维/环氧树脂复合材料夹层板的弯曲强度降低，并指出弯曲强度的降低可能由于裂纹长度的增加。Nandanwar 等[11]研究了不同跨厚比（10、20、32、48）对胶合板弯曲性能的影响，发现胶合板的弯曲弹性模量（modulus of elasticity，MoE）、断裂模量（modulus of rupture，MoR）均随着跨厚比的增大而增大，但增大幅度越来越小，并建议胶合板的三点弯曲性能测试的临界跨厚比为20。Li 等[12]研究了GLARE 层合板的弯曲破坏机理及损伤行为，结果表明：跨厚比通过影响复合材料的破坏模式来影响其弯曲力学性能；当跨厚比为14～24 时，GLARE 层合板发生有效的弯曲破坏；GLARE 层合板的弯曲破坏分为4 个阶段：（1）弹性变形阶段；（2）塑性变形阶段；（3）局部纤维断裂阶段；（4）分层阶段。

Zhu 等[13]采用有限元分析和实验方法研究了铝蜂窝、泡沫铝、聚氨酯弹性体夹芯层合复合材料箱梁的三点弯曲性能。徐学宏等[14]的研究表明缝合密度对缝合复合材料的弯曲性能影响较大。龚亮等[15]研究了热氧老化对三向正交复合材料弯曲性能的影响，并基于改进型随机过程模型得到预测三向正交复合材料弯曲强度的模型。冯景鹏等[16]指出2.5D 浅交直联Cf/Al 复合材料的弯曲失效机制为经向纱线被压断、纬向纱线产生挤压变形。Yin 等[17]的研究表明跨厚比的变化对三点弯曲梁初始断裂能释放率的影响很小，但跨厚比增大会使不稳定断裂能释放率略微下降。研究表明[18-19]不同类型的复合材料三点弯曲测试应选用不同的跨厚比。许多学者研究了碳纤维复合材料及其他复合材料[20-23]不同结构的弯曲力学性能，近年来玻璃纤维/树脂复合材料的用量越来越大，但针对玻璃纤维/树脂复合材料弯曲性能研究的文献报道较少，因此有必要对玻璃纤维/树脂复合材料弯曲力学性能进行研究。

本工作通过三点弯曲实验测试不同跨厚比高强玻纤复合材料单向板的弯曲性能，研究跨厚比对单向板弯曲强度、弯曲模量等性能的影响，通过分析弯曲破坏机制确定三点弯曲测试的临界跨厚比，基于实验数据进行拟合，得到任意跨厚比下单向板弯曲强度的预测公式及单向板弯曲破坏的失效准则。

1 实验材料与方法

1.1 实验材料

实验材料为中航工业基础技术研究院复合材料技术中心研制的S6C10-800/AC318 复合材料单向板，纤维体积分数为60%。其中纤维为南京玻璃纤维研究设计院生产的S6C10-800 高强玻纤，树脂为中航工业基础技术研究院复合材料技术中心研发的高韧性环氧树脂AC318。单向板弯曲试样规格72 mm×12 mm×1.7 mm，力学性能如表1。

表1 单向板力学性能Table 1 Mechanical properties of unidirectional plate

1.2 实验方法

参考ASTM D7264/D7264M—2015 标准，在Instron 5982 电子万能材料试验机进行弯曲性能测试，跨厚比α分别选定为10、16、20、26、32。

1.3 数据计算方法

（1）弯曲应力

根据ASTM D7264/D7264M—2015 标准，弯曲强度定义为最大载荷对应的跨距中点外表面的正应力。其中，跨距中点外表面的正应力按式（1）计算：

式中：σ为跨距中点外表面的弯曲正应力，MPa；P为载荷，N；L为跨距，mm；b为试样宽度，mm；h为试样厚度，mm。最大载荷Pm对应的跨距中点外表面弯曲正应力值即为弯曲强度σF。

（2）弯曲应变

跨距中点外表面正应变按式（2）计算：

式中：ε为跨距中点外表面正应变；δ为跨距中点的挠度，mm。

（3）弯曲模量

根据式（1）、式（2），将实验过程中连续记录的载荷-挠度数据转换成连续的应力-应变数据，并绘制弯曲应力-应变曲线。弯曲模量按式（3）计算：

式中：Ef为弯曲模量，GPa；Δε为弯曲应力-应变线性段上两个所选应变点之间的应变差，με；Δσ为与Δε对应的两个所选应变点之间的应力差，MPa。弯曲弹性模量计算选取的应变范围为1000～3000 με。

（4）弯曲应力的大挠度修正

当采用较大的跨厚比时，复合材料变形量较大，在支座处产生较大的端部载荷，导致应力-应变曲线非线性，此时需对弯曲应力公式进行大挠度修正，如式（4）所示。

（5）弯曲实验中的剪应力

当采用较小的跨厚比时，复合材料在发生弯曲破坏前可能由于层间剪切应力过高而提前发生分层破坏，故采用式（5）评估弯曲实验过程中的最大层间剪切应力。

式中：τ为弯曲实验过程中的最大层间剪应力，MPa；Pm为最大载荷，N。

2 结果与讨论

2.1 不同跨厚比的应力-应变曲线和失效模式

图1 和图2 分别为采用跨厚比α＝10、16、20、26、32 弯曲实验测得的单向板典型应力-应变曲线和断裂模式。由图1、图2 可知，采用不同的跨厚比时，单向板试样的应力-应变曲线和断裂模式存在显著差异。

图1 不同跨厚比单向板的典型弯曲应力-应变曲线Fig. 1 Typical stress-strain curves of unidirectional plates with different span-thickness ratios

跨厚比α＝10 时（图2（a）），应力-应变曲线在初始破坏前一直保持良好的线性关系，发生初始破坏后，应力-应变曲线斜率逐渐减小，并在达到最大应力水平后，应力骤降；试样的破坏模式为典型的层间剪切破坏，能明显分辨出试样分层损伤萌生于试样的中部，且分层沿长度方向逐渐向试样的两侧扩展，而试样的上、下表面并未发生破坏。这是由于跨厚比很小时，实验过程中试样内部层间剪切应力水平较高，且此时最大层间剪切应力与材料的层间剪切强度大小相当。

当跨厚比α＝16 时（图2（b）），试样从最初加载到最终破坏，应力-应变曲线明显保持线性关系。试样的破坏模式为混合破坏，明显分辨出试样内部产生分层，少量试样出现上表面压缩破坏或下表面拉伸破坏，破坏机制为试样上、下表面的损伤萌生后迅速演化为分层破坏，导致宏观失效模式以分层为主。跨厚比变大时，试样内部应力分布发生变化，由小跨厚比的以层间剪切应力为主转变为弯曲应力占主导，但层间剪切应力的影响依旧不可忽略。

跨厚比α＝20 时（图2（c）），试样从最初加载到最终破坏，应力-应变曲线一直保持线性关系；试样的破坏模式为以上表面压缩破坏为主，存在少量分层，试样发生轻微的纤维横向劈裂，一条劈裂主裂纹由试样跨距中点处沿纤维方向向两端扩展，扩展至试样长度的1/3 处，并且裂纹宽度极小，断口较粗糙，破坏机制为试样上表面严重压缩损伤诱发分层破坏，导致宏观失效模式表现为上表面压缩和分层的混合破坏模式。随着跨厚比的进一步增大，试样内部弯曲应力逐渐增大，层间剪切应力进一步减小，层间剪切应力对材料弯曲性能测定的影响便可忽略。

当跨厚比α＝26 时（图2（d）），试样的应力-应变曲线呈现一定的非线性特征，这是由于试样产生的大挠度变形导致的。试样的破坏模式为上表面压缩破坏和下表面拉伸破坏，但是下表面的拉伸破坏是由于上表面压缩破坏后损伤扩展导致的，纤维横向劈裂比较明显，多条劈裂裂纹萌生于试样跨距中点处，且一直沿纤维方向扩展至试样长度的1/2～1/3 处为止，劈裂裂纹宽度比跨厚比α＝20 时变大，同时存在极少量分层。当跨厚比α＝32 时（图2（e）），试样的应力-应变曲线的非线性特征更加明显，这也是由于试样产生的大挠度变形导致的。试样的破坏模式为上表面压缩破坏和下表面拉伸破坏，仍以上表面压缩破坏为主，纤维横向劈裂更加严重，多条劈裂裂纹由萌生位置沿纤维方向向两端迅速扩展，最终几乎贯穿整个试样的长度方向，且劈裂裂纹宽度明显增大，分层损伤程度再次降低。

图2 不同跨厚比的典型断裂模式（a）α= 10；（b）α= 16；（c）α= 20；（d）α= 26；（e）α= 32；（1）受拉伸的下表面；（2）受压缩的上表面Fig. 2 Typical fracture modes with different span-to-thickness ratios （a）α= 10；（b）α= 16；（c）α= 20；（d）α= 26；（e）α= 32；（1）lower surface of specimen under tension； （2） upper surface of specimen under compression

通过分析试样宏观断口可看出，随着跨厚比的增加，试样分层损伤程度逐渐降低，而纤维横向劈裂程度增加。此外，跨厚比α≤20 时，随跨厚比的增加，应力-应变曲线越来越符合线性关系，当α＞20，应力-应变曲线不再符合线性关系，跨厚比为16、20 时，从试样开始加载到最终破坏，应力-应变曲线明显符合线性关系，跨厚比为10 时，应力-应变曲线的非线性主要是分层损伤的萌生和扩展导致的，而在跨厚比为26、32 时，应力-应变曲线的非线性主要是大挠度变形导致的。

2.2 不同跨厚比的弯曲强度

表2 给出了不同跨厚比试样的弯曲强度和最大载荷下对应的层间剪切应力。其中，跨厚比α＝10、16 下的挠度较小，弯曲强度无须进行大挠度修正。跨厚比α＝20、26、32 下试样发生较大的挠曲变形，弯曲强度需要进行大挠度修正。

表2 不同跨厚比试样的弯曲强度及破坏载荷下对应的层间剪应力Table 2 Bending strength with different span-to-thickness ratios and corresponding interlaminar shear stress under failure load

图3 为试样破坏时其中面的层间剪切应力与跨厚比的关系，图4 为试样弯曲强度与跨厚比的关系。随着跨厚比的增加，弯曲强度随之增加，但弯曲强度的增加幅度越来越小；随着跨厚比的增加，试样破坏时中面处的最大层间剪切应力迅速降低。可见单向板的弯曲强度不仅取决于其本身的材料属性，而且会随着材料断裂模式、受力状态的变化而变化。

图3 不同跨厚比的单向板破坏时跨距中点的层间剪应力Fig. 3 Interlaminar shear stress at the span midpoint of unidirectional plates with different span-thickness ratios

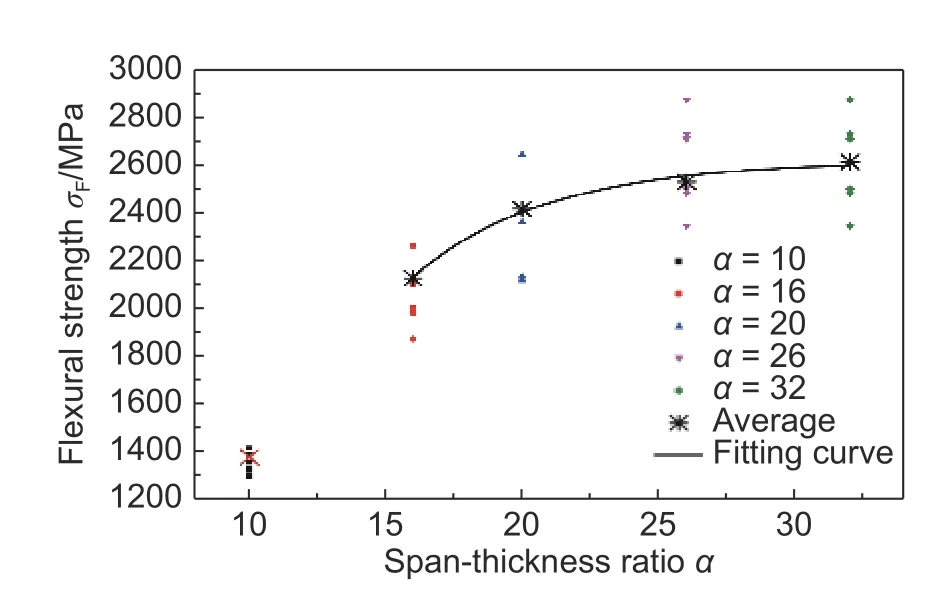
图4 单向板的弯曲强度与跨厚比的关系Fig. 4 Relationship between the bending strength and the span-thickness ratio of a unidirectional plate

当跨厚比α＝10 时，试样破坏时的层间剪切应力已经逼近层间剪切强度（经测试，所用材料的层间剪切强度为76.3 GPa），试样的破坏是由于发生了分层，测得的弯曲强度最低，根据弯曲强度的定义，由于试样并未发生上、下表面的破坏，因此，测得的弯曲强度是一个虚假的弯曲强度值；跨厚比α＝16 与α＝10 相比，测得的强度显著增加了51.76%，观察断口形貌虽然宏观上主要表现为层间分层破坏，但该分层破坏是由于上、下表面的损伤诱发的，此时测得的弯曲强度是有效的。

跨厚比α＝20 时，试样的断裂模式转变为以压应力破坏为主导，伴随有少量的分层，试样破坏时其中面的层间剪切应力大幅度降低，这是由于试样的破坏载荷随着跨厚比的增大而减小（如表2 所示），根据式（5），试样的破坏载荷减小，而试样的宽度、厚度不变，从而导致层间剪切应力减小，此时的弯曲强度也比α＝16 增加了13.95%，说明在弯曲实验中采用较大的跨厚比可有效地减小层间剪切应力对弯曲强度的影响。

当跨厚比α＞20 时，单向板的弯曲强度随着跨厚比增加幅度很小，这是由于高跨厚比导致了复合材料沿纤维方向发生劈裂较严重，劈裂破坏了复合材料的整体性，从而最终导致了弯曲强度增幅的下降；跨厚比的增大还可能会导致复合材料基体内部裂纹增多，裂纹长度增大，裂纹尖端应力集中加剧，裂纹扩展阻力减小，较容易扩展至基体与纤维的界面处，使得复合材料被破坏，导致力学性能下降，弯曲强度增加幅度减小。综上所述，跨厚比主要通过影响试样中的应力分布，导致断裂模式的差异，进而影响测得的弯曲强度值。

根据α＝16、20、26、32 下的弯曲强度值，进行数据拟合，得到了以跨厚比α为自变量表示单向板弯曲强度的理论公式（6），拟合曲线如图4 所示，由图4 可见，式（6）可很好地描述弯曲强度随跨厚比的变化。

σF=2622−12755•exp(−0.2α) (6)

2.3 不同跨厚比的弯曲模量

表3 为不同跨厚比的单向板弯曲模量。由表3 可见，随着跨厚比的增加，单向板的弯曲模量先增大后减小。

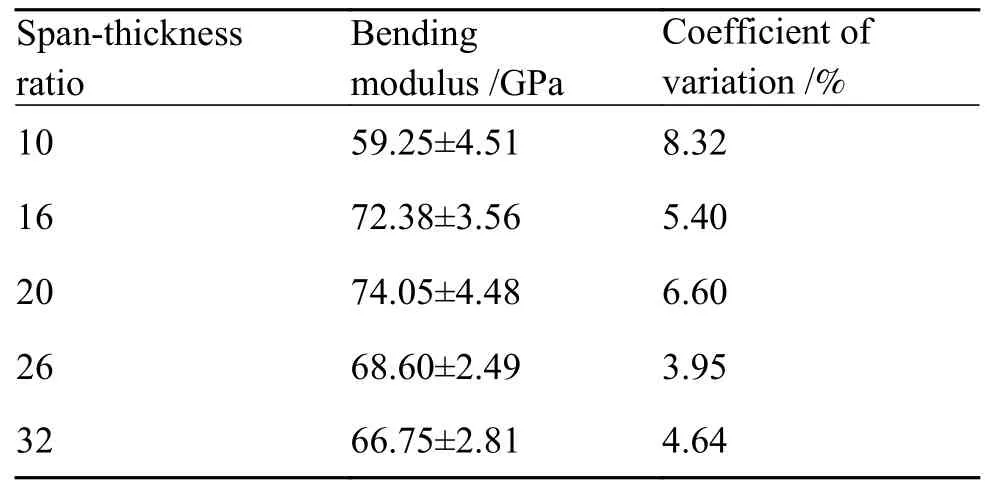
表3 不同跨厚比的复合材料弯曲模量Table 3 Bending modulus of composite materials with different span-thickness ratios

当跨厚比α＝10 时，测得的模量远小于其他跨厚比时的模量，这是由于弯曲实验中试样不可避免地受到剪应力作用产生变形，测出的挠度既包含了弯曲挠度，还包含了剪切挠度，但在实验数据处理计算时按纯弯曲载荷作用考虑，忽略了剪切载荷作用的影响，因此计算出的模量要比材料的实际模量低；并且跨厚比越小，剪切载荷引起的挠度就越大，从而小跨厚比测得的模量远小于较大跨厚比测得的模量。跨厚比α＝20 时，单向板的弯曲模量最大，为74.05 GPa，可见复合材料的弯曲模量是一个与跨厚比有关的参数，不能当作材料的固有属性。

当跨厚比α＞20 时，测得的弯曲模量略有减小，这可能由于跨厚比增大会导致复合材料变形量增大，因弯曲模量的计算公式是基于复合材料应变呈线性变化这一假设的，变形量过大时，复合材料应变呈现出非线性分布，弯曲模量计算可能不再成立，最终得到的弹性模量就略有减小。

2.4 高强玻纤弯曲破坏失效准则

基于跨厚比为16、20、26、32 下测试的弯曲性能结果，改进了一种经典的复合材料失效判据——二维Hashin 准则中适用于纤维压缩破坏模式的失效准则，其未改进的表达形式如式（7）所示，得到了适合于高强玻纤复合材料单向板的失效判定准则，拟合结果如图5 所示。

图 5 基于实验数据改进Hashin 准则的拟合结果Fig. 5 Improving fitting results of Hashin criterion based onexperimental data

纤维压缩破坏模式(σ11＜0)：

由于单向板在进行三点弯曲实验时，材料的主要破坏模式为纤维压缩破坏，且伴随有不同程度的层间分层，改进后的单向板弯曲破坏的失效判定准则如式（8）所示，改进后的准则考虑了层间分层的影响。

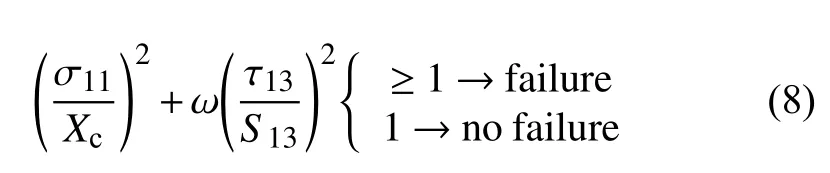
式中：σ11为α＝16、20、26、32 试样测试得到的弯曲强度；τ13为α＝16、20、26、32 弯曲测试过程中的最大层间剪应力（如表2 所示）。图5 中的拟合结果为拟合参数：ω＝4.40。

3 结论

（1）随跨厚比的增加，单向板的弯曲强度增大，但增加幅度越来越小，而弯曲模量先增大再减小，在跨厚比α＝20 时达到最大值，为74.05 GPa。跨厚比主要通过影响试样内部的应力分布，使其断裂模式各有差异，进而影响测得的弯曲性能。

（2）随着跨厚比的增加，弯曲性能受剪切应力的影响越小，其断裂模式由以剪切导致的分层破坏为主（α＜20 时）逐渐转变为以拉应力和压应力导致的弯曲破坏为主（α≥20），但当跨厚比过大（α＞20）时，试样沿纤维方向发生严重劈裂。

（3）当α≤20 时，跨厚比越大，应力-应变曲线越符合线性关系，当α＞20 时，应力-应变曲线不再符合线性关系；单向板三点弯曲性能测试的临界跨厚比建议取20；基于实验数据拟合，得到了用于预测单向板在不同跨厚比下弯曲强度的公式及适用于高强玻纤/树脂复合材料单向板的三点弯曲破坏的失效判定准则。