飞机前轮转弯系统潜在故障预警方法研究

黄世杰，蔡景，何盛

（1.南京航空航天大学民航学院，南京210016）（2.中国东方航空江苏有限公司飞机维修部，南京211113）

0 引言

在飞机的地面运行过程中，机组要控制飞机在地面的滑行，将飞机停放在目标位置。在此过程中飞机转弯发挥着关键的作用。飞机前轮转弯系统不仅可以控制飞机在地面的灵活滑行，而且一定程度上还可以避免轮胎磨损及局部高温，是现代民用飞机和大多数军用飞机实现地面方向控制的常用方法。飞机在地面滑行时如果前轮转弯失效，轻则导致航班延误，飞机停留在跑道上，影响其他飞机的正常起飞和降落；重则导致轮胎严重磨损甚至爆破，威胁机上人员的安全。为了预防飞机前轮转弯系统出现故障，现有的飞机计划维修体系对前轮转弯系统采用定期检查的方法，实践证明，该方法虽然可以提前发现诸如前轮磨损、胎压差值较大等外部故障，但对于管路渗漏、活门故障等潜在故障基本无法提前识别。其原因是这类潜在故障具有很强的隐蔽性，不会在短时间内直接影响功能的使用。但当潜在故障累积到一定程度时，就会导致“转弯困难或失效”，这种故障由于在定期检查中基本不能被提前检测到故障征兆，而往往被误认为突发随机故障。但实际上，根据飞机前轮转弯系统的结构和原理可知，转弯困难或失效故障模式具有渐变式的特点。因此，可以通过挖掘快速存取记录器（Quick Access Recorder，简称QAR）中记录的数据，找到反映转弯失效故障征兆的特征参数，实现对故障的提前识别。

国内针对飞机前轮转弯系统开展了一定的研究。例如，梁建平和孙贵杨针对波音737NG 飞机前轮跑偏故障分析了其发生的原因、形式并总结了排除该故障的常规方法；金磊通过对某型飞机“漂移”故障机理进行分析，提出了应对漂移故障的改进措施；罗刚通过对A320 飞机的原理进行介绍，针对A320 滑行中非指令性方向偏转的故障，总结了前轮转弯系统排故经验；薛海红等以某型飞机的前轮转弯系统为例，基于故障模式及影响分析（Failure Mode and Effects Analysis，简称FMEA）建立了贝叶斯网络模型，可以有效融合多源信息对前轮转弯系统进行故障诊断；Dai Zhi‑yong 等针对飞机ABS 系统提出了一种基于模型和灰色关联分析相结合的诊断策略，经验证拥有相对准确的诊断准确度；Liu Kuijian 等针对起落架收放机构提出了一种基于深度学习模型的多源信号特征融合方法，具有较好的特征融合能力和较高的诊断精度。可见，目前国内针对飞机前轮转弯系统故障的研究都集中在故障诊断方面，未见有关故障预警方面的研究报道。国外针对起落架收放和刹车系统故障诊断和预测有较多研究，但未找到关于前轮转弯系统故障诊断的相关研究。

飞机QAR 数据在故障预测方面已有广泛的应用。因此，本文针对飞机前轮转弯系统在现有计划维修体系下故障具有隐蔽性的特点，通过挖掘QAR 数据，研究飞机前轮转弯系统“转弯困难或失效”故障的潜在特征，实现对前轮转弯系统关键潜在故障的提前预警。

1 特征参数提取

1.1 QAR 参数获取

QAR 是飞机机载记录系统中的快速存储装置，可实现飞行数据的便利存取。QAR 记录的参数在飞机落地后由地面人员将数据拷贝或者通过无线快速存取记录器（Wireless Quick Access Re‑corder，简称WQAR）下传，经过专门的译码软件处理后，为飞机性能分析、系统状态监控、故障诊断及飞行品质监控提供数据支持。

根据飞机前轮转弯系统的工作原理，“转弯困难或失效”故障的预警主要跟表征飞机转弯角度的参数有关。QAR 记录了许多与前轮转弯相关的参数，结合其采样原理本文选择以下特征参数（如表1 所示）分析“转弯困难或失效”故障的潜在表现。

表1 前轮转弯参数列表Table 1 List of front wheel turning parameters

1.2 前轮转弯的数据采集特点

根据飞机前轮转弯系统的结构和原理，并分析其典型故障及原因发现：管路渗漏、安全活门故障、缺少润滑等可能导致前轮转弯指令值与实际值出现延后及偏差，从而造成转弯困难或失效。因此，选取前轮转弯指令参数和实际角度参数，通过分析正常情况和故障情况下两个参数之间的相关性特征，建立飞机前轮转弯系统的故障预警方法。通过分析QAR 数据发现：机载的两套刹车和转弯控制组件（Braking/Steering Control Unit，简称BSCU）中，当BSCU2 处于接通状态时指令值恒为0，这与数据采集的来源有关，因此BSCU1 处于未接通时记录的数据并非前轮转弯的实际值。一般情况下，1 次航班中BSCU1 和BSCU2 各出现1次持续一段时间的接通，如果出现二者多次交替接通的情况，为了保证所分析数据的连续性，只需要选择BSCU 1 接通时持续时间最长的一段数据进行分析即可。

1.3 数据预处理

原始航班数据经过译码后导出的QAR 数据包含了表头、时间列等与分析无关的信息，而且不同参数由于采样频率不同，会导致某些参数存在缺省的情况，因此要对译码后的QAR 数据进行预处理。

参数NWS_ORDER_ANG 和NWS_WHEEL_ANG 的采 样频 率为4 Hz，BSCU1_EGD 和BS‑CU2_EGD 的采样频率为1 Hz，故二者存在缺省。该缺省值由于记录的并非数据而是BSCU 的接通状态，当存在BSCU 切换时，采用上一采样值填补的方法最多影响3 条（即0.75 s）数据，且查看大量航班数据发现，一个航班中BSCU1 和BSCU2 的切换最多出现3 次，这对于整个航班动辄上万条数据来说是可以忽略的，故选择该缺省值填补方法处理缺省数据。处理后的部分数据如表2 所示。

表2 部分QAR 数据展示Table 2 Part of QAR data display

2 基于Pearson 相关性系数的故障预警方法

通过分析“转弯困难或失效”故障案例，发现该类故障存在一个共同的故障表现：驾驶员的转弯指令得不到准确地执行，即驾驶员的指令值与实际执行值之间存在不一致。不一致可以从两个方面考虑：（1）指令值与实际值存在漂移（指令延后）；（2）指令值与实际值相关性低。

2.1 QAR 数据初始分析

根据有故障航班数据，绘制指令值和实际值的变化图，如图1 所示，可以看出：故障航班中存在指令值和实际角度值明显偏离的情况。

图1 故障航班中所研究参数的变化情况Fig.1 Changes of the parameters studied in the faulty flight

绘制正常航班对应参数变化图，如图2 所示，可以看出：即使正常航班也存在指令值和实际值指令漂移较大的情况，故“指令值与实际值指令漂移较大”不能作为故障的征兆，可通过分析指令值与实际值之间的相关性特点，得到故障的特征。

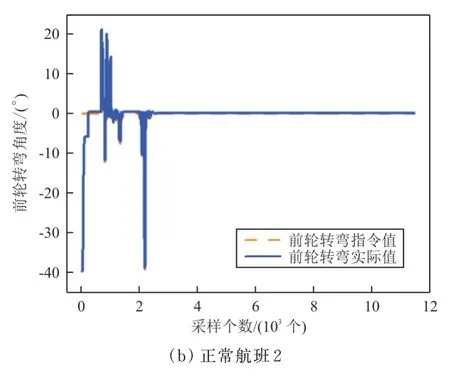
图2 正常航班中所研究参数的变化情况Fig.2 Changes of parameters studied in normal flight

2.2 基于指令值与实际值相关性的预警分析

2.2.1 Pearson 相关性系数

统计学中有三种常见的相关性系数：Pearson积差相关性系数用于量度两个变量和之间的线性相关；Spearman 秩相关性系数利用两变量的秩次大小作线性相关分析，但效能不如前者；Ken‑dall 秩相关性系数适用于两个变量均为有序分类的情况。

Pearson 相关性系数是英国统计学家Pearson于20 世纪提出的一种用于度量两个变量和之间的相关（线性相关）程度的方法，可以用来进行特征选择、模型预测、寻找最优解等，具有广泛的应用领域。本文选择Pearson 相关性系数进行分析。

假设两个变量、分别是一个数集，则和之间的Pearson 相关性系数可以通过式（1）进行计算。

式中：ρ为、的Pearson 相关性系数；（）和μ均为的期望值；σ为的方差；（）和μ均为的期望值；σ为的方差；cov（，）为、的协方差。

计算所得的相关性系数的绝对值越大，相关性越强。相关性系数越接近1 或-1，相关性越强；相关性系数越接近0 则相关性越弱。当相关性系数为0 时，和两变量无关系；当一个的值增大（减小），另一个值增大（减小），两个变量为正相关，相关性系数在0 与1 之间；当一个的值增大（减小），另一个值减小（增大），两个变量为负相关，相关性系数在-1 与0 之间。

2.2.2 相关性分析

根据历史数据绘制指令值和实际值的关系图，如图3 所示，可以看出：二者基本呈线性关系，符合Pearson 相关性系数的使用条件。

图3 指令值和实际值关系变化图Fig.3 Diagram of the change of the relation between instruction value and actual value

在前轮转弯过程中，如果转弯指令发出后，2 s 内系统没有做出相应的动作，飞行员可以明显感知到存在指令延后，因此对于指令延后的分析范围设定为2 s。由于指令值和实际值的采样频率为4 Hz，2 s 对应8 个数据位，可以对实际值延后0~7 个数据位分别与指令值进行相关性分析。

将指令值和实际值作为Pearson 相关性分析方法的输入数据集。首先对总计106 个连续无故障航班的QAR 数据进行相关性分析计算，得到的指令值和延后不同位数的实际值的相关性系数如表3 所示。

表3 连续正常航班的相关性分析结果Table 3 Correlation analysis results of continuous normal flights

从表3 可以看出：大多数情况下，无延后的实际值与指令值之间的相关性系数最大，少数情况下，1~2 个数据位延后的实际值与指令值之间的相关性系数最大。表明前轮转弯中数据延后的现象并不明显或者可以认为指令延后的现象可以忽略；另外，各个正常航班对应的相关性系数均在0.9 以上，不同延后下的相关性系数变化范围在0.05 以内，表明指令值与实际值之间具有高度的相关性，符合前轮转弯系统正常工作状态的实际情况。

在故障案例中，分析故障航班的QAR 数据与该次航班之前的连续11 个航班的数据的相关性，分析结果如表4 所示。

表4 存在故障的连续航班相关性分析结果Table 4 Correlation analysis results of continuous flights with faults

从表4 可以看出：相关性系数最大时数据延后位数基本为1 个，但值与不延后时相差极小，可认为数据延后现象并不存在；故障前相关性系数基本在0.8 以上，其中延后不同位数的相关性系数变化范围值均在0.06 以内，且在靠近故障航班时值明显变大。对于有故障航班，系数值低至0.55 左右，表明指令值和实际值相关性低，出现了指令偏移；且延后不同位数的相关性系数变化范围为0.18，与正常航班表现出明显差别，表明数据的连续性也受到了影响。

11 个航班延后0~7 位数据相关性系数变化区间的长度如图4 所示。

图4 11 个航班的相关性系数变化区间长度图Fig.4 Variation length of correlation coefficient of 11 flights

综合上述分析结果，可得：

（1）当某航班指令值和实际值的相关性系数较低（低于0.8）时，表明前轮转弯系统可能存在潜在故障，需要在飞行中给予一定的关注；当连续出现较低情况时，极有可能出现了潜在故障，需要停飞检查。

（2）当某航班指令值和实际值的相关性系数较低时，且将实际值延后0~7 位与指令值的相关性系数变化范围超过0.1（保守估计），表明二者之间的连续性受到影响，出现指令偏移，极有可能存在潜在故障，需要对前轮转弯系统进行检查以免影响飞行安全。

需要注意的是，上述结论是基于整个航班数据得到的，且相关性系数计算的准确度与数据量呈正相关的关系，飞行前期由于数据量较少可能会产生虚警，因此采用该方法实现对前轮转弯系统的实时监控尚具有一定的挑战性。

3 实例验证

以某航空公司相同机型的飞行数据为例进行验证。由于前轮转弯系统的故障很少，为了验证“转弯困难或失效”潜在故障与“指令值与实际值”相关性系数之间的关联性，在对该飞机的前轮转弯问题进行定期维修前，收集和整理该飞机最近13 个航班的QAR 数据，对其指令值和实际值作相关性进行分析，结果如表5 所示。

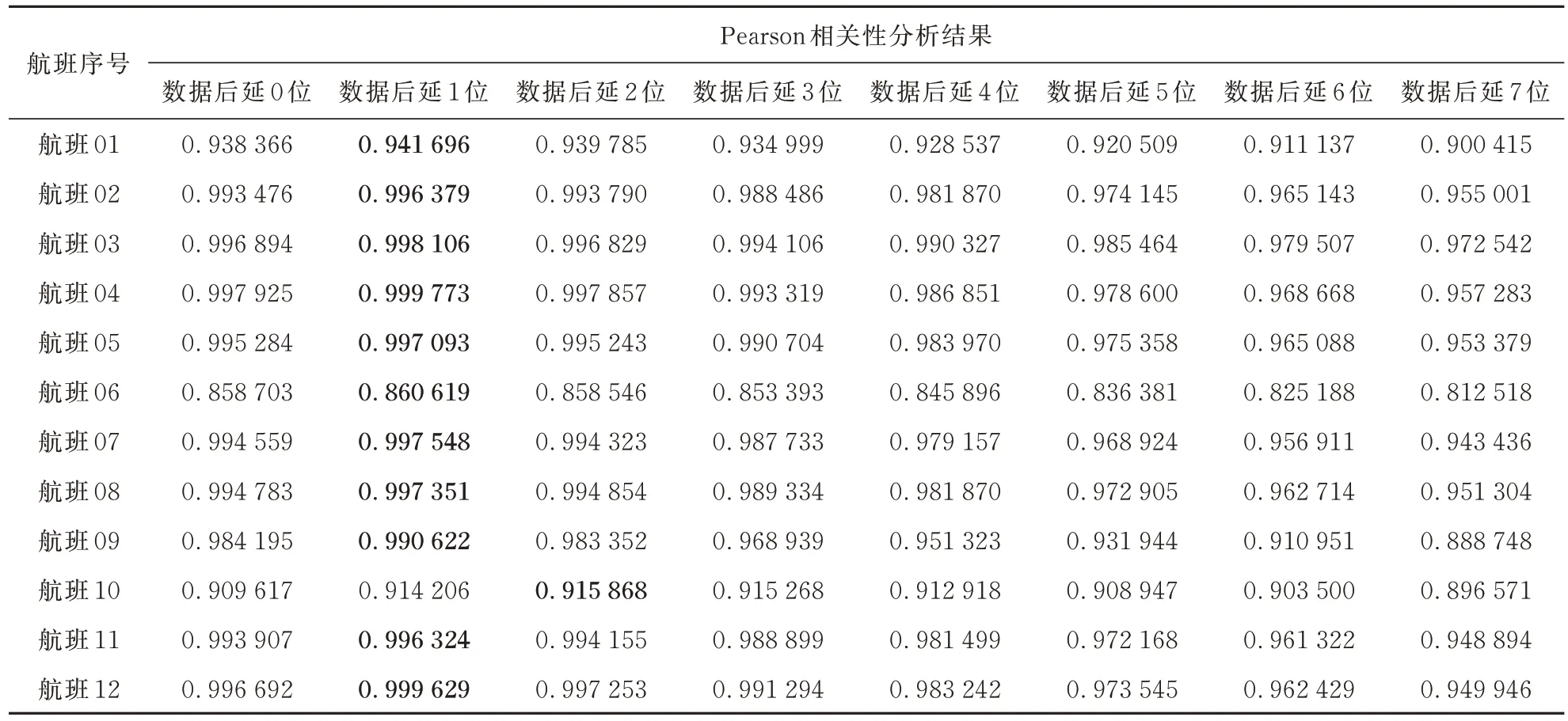
表5 用于验证的连续航班的相关性分析结果Table 5 Correlation analysis results of consecutive flights for validation

从表5 可以看出：除编号为06 的航班外，其余航班的相关性系数均在0.9 以上，编号为06 的航班的相关性系数也都在0.8 以上，因此可以认为该飞机前轮转弯系统无潜在故障。将这一分析结果与该航空公司的维护人员执行定期维修时的检查结果完全符合，证明所提预警方法对于该机型的有效性。

另外，由于上述所使用的数据均来自相同型号的飞机，所得结论是否适用于其他型号的飞机有待相关数据佐证，本文所提出的分析方法可供参考。

4 结论

（1）根据飞机前轮转弯系统的工作原理和故障特点，选取转弯角度指令值和实际值作为预警监测参数，采用Pearson 相关性分析方法，得出“转弯困难或失效”的故障规律及阈值：相关性系数低于0.8 或实际值延后0~7 位时变化范围超过0.1，实现了对飞机前轮转弯系统潜在故障的预警。

（2）利用同型号飞机QAR 数据对本文所提预警方法进行了验证，预警结果与维修人员实际检测结果一致，表明了预警方法的有效性。