求解抽象函数问题常用的五种策略

陈海燕

(甘肃省张掖市实验中学)

所谓抽象函数,是指没有给出函数解析式,但给出了函数的部分性质或运算法则的函数.因为抽象函数问题具有题设抽象、构思新颖、综合程度高等特点,所以它是学习函数时的一大难点,大多数学生在解题时往往无从下手、束手无策.根据以往的经验,解题的关键是引导学生对症下药,因题制宜,随题应变,利用赋值、“穿脱”、数形结合、模型、构造等策略处理,问题就迎刃而解了.下面就这些解题“大招”进行具体例析,供读者参考.

1 赋值策略

赋值策略是指根据题目所给条件,通过观察、分析、类比、联想等思维活动,对变量赋予特殊值,然后进行合理的运算,达到解决问题的目的.这种策略在解决抽象函数问题时具有独特的功效,它简单方便,是探求抽象函数问题的一种常用的思维策略.

例1若奇函数f(x)(x∈R)满足f(2)＝1,f(x＋2)＝f(x)＋f(2),则f(1)＝( ).

抽象函数求函数值需用赋值法,由奇函数的性质得f(-1)＝-f(1),结合题设条件f(2)＝1,f(x＋2)＝f(x)＋f(2),令x＝-1,得f(1)＝f(-1)＋1,即f(1)＝-f(1)＋1,从而2f(1)＝1,所以f(1)＝,故选D.

赋值法是演绎推理下的一种特殊化策略,解题时若能根据具体情况,有目的、有方向、合理巧妙地对某些自变量赋予一些确定的特殊值,往往能使问题有效获解.

例2已知函数f(x)的定义域为R,且对任意a,b∈R,都有f(a＋b)＝f(a)＋f(b),f(x)＜0在(0,＋∞)上恒成立,则函数f(x)的奇偶性为( ).

A.奇函数

B.偶函数

C.非奇非偶函数

D.既是奇函数又是偶函数

函数f(x)的定义域为R,所以定义域关于原点对称,判断奇偶性的关键是求f(-x)＝f(x)或f(-x)＝-f(x).结合题设等式f(a＋b)＝f(a)＋f(b),可以令a＝x,b＝-x,这样会出现f(0),故第一步先求f(0).

因为对任意a,b∈R,都有f(a＋b)＝f(a)＋f(b),所以令a＝b＝0,得f(0)＝2f(0),即f(0)＝0.再令a＝x,b＝-x,得f(0)＝f(x)＋f(-x),即f(-x)＝-f(x),所以函数f(x)为奇函数,故选A.

赋值法是解决抽象函数问题常用的方法,它适用于抽象函数的求值,判断抽象函数的奇偶性等,有时还需要多次赋值.

2 “穿脱”策略

加上函数符号“f”即为“穿”,去掉函数符号“f”即为“脱”.对于有些抽象函数,可根据函数值相等或函数的单调性,实现对函数符号“f”的“穿脱”,以达到简化解题的目的.

例3已知奇函数f(x)是定义在(-2,2)上的减函数,若f(m-1)＋f(1-2m)＞0,则实数m的取值范围为( ).

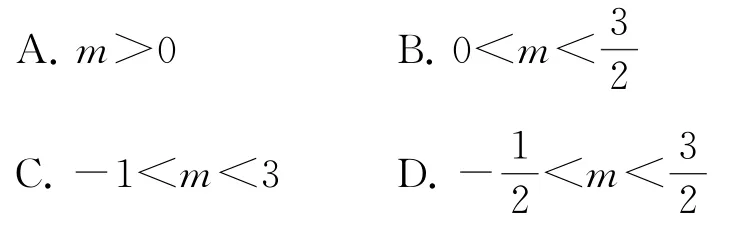
由f(m-1)＋f(1-2m)＞0,且f(x)是奇函数,得f(m-1)＞-f(1-2m)＝f(2m-1),又因为f(x)是定义在(-2,2)上的减函数,故-2＜m-1＜2m-1＜2,解得0＜m＜,故选B.

移项的目的是利用奇函数的性质解题,也为脱去“f”做准备,过程环环相扣,层层递进,逻辑关系紧密,这类题目只要掌握其规律,往往水到渠成.

例4已知函数f(x)是定义在(0,＋∞)上的增函数,且满足对于任意的正实数x,y,都有f(xy)＝f(x)＋f(y),且f(2)＝1.

(1)求f(8)的值;

(2)解不等式f(x)＞f(x-2)＋3.

第(1)问求f(8)的值,合理赋值即可.第(2)问解不等式可以利用f(x)的单调性“穿脱”求解,但这之前必须利用题设等式将不等式右边合并.

(1)在f(xy)＝f(x)＋f(y)中,令x＝y＝2,得f(4)＝2;令x＝2,y＝4,得f(8)＝3.

(2)f(x)＞f(x-2)＋3⇔f(x)＞f(x-2)＋f(8)⇔f(x)＞f[8(x-2)].

因为函数f(x)是定义在(0,＋∞)上的增函数,则x＞8(x-2)＞0,所以2＜x＜从而原不等式的解集为(2

涉及抽象函数的单调性求解不等式的题目,我们常常利用函数f(x)的单调性,脱去函数符号“f”,将函数值的不等式转化为自变量的不等式求解.

3 数形结合策略

一般来说,抽象函数无图像,但可根据题设中所给的抽象函数性质,画出符合题意的草图,通过观察、对比,运用数形结合思想全面判断,并做定量分析,可使抽象函数形象化、具体化、直观化,从而减少推理、计算量.

例5若函数f(x)为R 上的奇函数,且在(0,＋∞)上为增函数,有f(2)＝0,则的解集为( ).

A.(-2,0)∪(0,2)

B.(-∞,-2)∪(0,2)

C.(-∞,-2)∪(2,＋∞)

D.(-2,0)∪(2,＋∞)

因为f(x)是R上的奇函数,所以f(x)的图像关于原点对称,根据题设条件可以画出函数f(x)在R 上的草图,如图1所示.

图1

解决数学抽象问题,直观永远是第一准则,要培养学生的数学抽象能力,离不开图形的直观性、形象性,有了直观才能想象.

例6已知定义在R 上的奇函数f(x),当x2＞x1＞0 时,f(x2)＜f(x1),且f(1)＝0,求不等式(2x-1-1)f(x)≥0的解集.

由题设条件可知,函数f(x)在(-∞,0)和(0,＋∞)上均为减函数,故画出函数f(x)在R 上的草图,如图2 所示,现分类讨论如下.

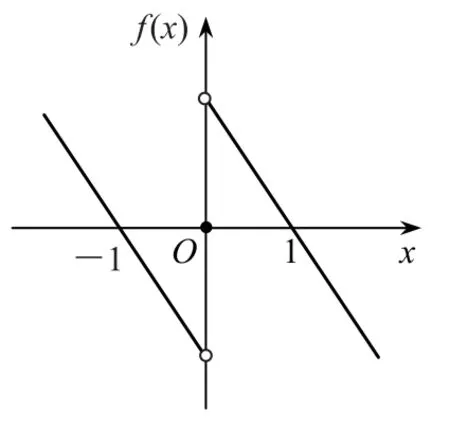
图2

当x≤-1 时,x-1≤-2,2x-1≤2-2＝,故2x-1-1＜0,但f(x)≥0,故满足不等式(2x-1-1)f(x)≥0的只有x＝-1.

当-1＜x≤0时,-2＜x-1≤-1,＜2x-1≤,故2x-1-1＜0,但f(x)≤0,故满足不等式

当0＜x≤1时,-1＜x-1≤0＜2x-1≤1,故2x-1-1≤0,但f(x)≥0,故满足不等式(2x-1-1)·f(x)≥0的只有x＝1.

当x＞1时,x-1＞0,2x-1＞1,故2x-1-1＞0,但f(x)＜0,不满足不等式(2x-1-1)f(x)≥0.

综上,不等式(2x-1-1)f(x)≥0 的解集为[-1,0]∪{1}.

草图是撬开分类讨论的有力杠杆,既省时省力,又直观明了.草图只要满足题意越简单越好,依靠数形结合思想解决抽象函数问题是培养学生抽象思维能力的主要途径.

4 模型策略

亚里士多德说过:“我们的思维是从与正在寻求的事物相类似的事物、相反的事物或者与之相接近的事物开始进行的,以后便追寻与之相关联的事物,由此产生联想.”模型化策略,就是根据题设所给的抽象函数性质,通过联想与类比,大胆猜想生成抽象函数的原始模型,作出目标猜想,利用模型函数的有关性质去探索解题方法.对于选择题和填空题,可用模型函数直接解决.对于解答题,模型函数只能起到启迪思路、指导解题的作用,解题时还必须从题设条件出发加以演绎推理,再证明或运算,切不可用特殊代替一般,发生逻辑上的错误.

例7定义在R上的函数f(x)对任意x,y∈R,满足f(x＋y)＝f(x)f(y),当x＜0时,f(x)＞1,则函数f(x)在[a,b]上( ).

A.有最小值f(a) B.有最大值f

C.有最小值f(b) D.有最大值f(b)

根据题设知指数函数f(x)＝满足条件,其在R上为减函数,所以函数f(x)在[a,b]上有最小值f(b),最大值为f(a),故选C.

例8设定义在R上的函数f(x)对于任意x,y都有f(x＋y)＝f(x)＋f(y),且f(1)＝-2,当x＞0时,f(x)＜0.

(1)判断f(x)的奇偶性,并加以证明;

(2)试问:当-3≤x≤3时,f(x)是否有最值.如果有,求出最值;如果没有,说明理由.

对于任意x,y都有f(x＋y)＝f(x)＋f(y),可猜想f(x)＝kx,由当x＞0 时,f(x)＜0,知k＜0,所以问题(1)(2)的答案可大胆猜想如下:(1)函数f(x)是奇函数;(2)函数f(x)在R上是减函数.

(1)令x＝y＝0,可得f(0)＝0,再令y＝-x,则f(0)＝f(-x)＋f(x),所以f(-x)＝-f(x),所以f(x)为奇函数.

(2)设-3≤x1＜x2≤3,令y＝-x1,x＝x2,则

因为x＞0时,f(x)＜0,故f(x2-x1)＜0,即

所以f(x2)＜f(x1),所以f(x)在区间[-3,3]上单调递减,所以当x＝-3时,f(x)有最大值为

当x＝3时,f(x)有最小值为f(3)＝-6.

“模型”策略是顺藤摸瓜,未做先知,预先看穿问题本源,洞穿问题实质,大多数抽象函数方程都有其对应的初等函数,常见抽象函数方程对应的原型函数如表1所示.

表1

5 构造策略

在求解抽象函数单调性的过程中,首先应熟悉单调性的定义,即在某一区间D上,当x1,x2∈D,且x1＜x2时,函数f(x)有f(x1)＜f(x2)(或f(x1)＞f(x2))则称函数f(x)在D上为增函数(或减函数);其次需见缝插针地构造一个“大”自变量,如“x1＝(x1-x2)＋x2”“x2＝(x2-x1)＋x1”“x1＝·x2”或“x2＝·x1”等,这样才可以充分利用题设条件,巧妙利用定义证明单调性问题.

例9已知函数f(x)的定义域为[-1,1],若对任意x,y∈[-1,1],都有f(x＋y)＝f(x)＋f(y),且当x＞0时,f(x)＞0.

(1)判断并证明函数f(x)的奇偶性;

(2)判断并证明函数f(x)在[-1,1]的单调性.

第(1)问用赋值法证明;第(2)问中转化x2＝(x2-x1)＋x1,有意构造出x2-x1＞0使解题豁然开朗,因为这样就可以利用题设条件当x＞0时,f(x)＞0顺利解题.

(1)令x＝y＝0,得f(0)＝0,再令y＝-x,得f(-x)＝-f(x),所以函数f(x)为奇函数.

(2)由题意,设-1≤x1＜x2≤1,则

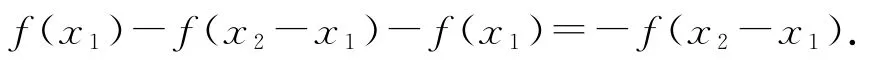
因为x2-x1＞0,所以f(x2-x1)＞0,-f(x2-x1)＜0,即f(x1)＜f(x2),所以函数f(x)在[-1,1]上单调递增.

构造x2＝(x2-x1)＋x1,解决了利用单调性定义证明中的难点.

例10函数f(x)的定义域为(0,＋∞),且对一切x＞0,y＞0,都有f＝f(x)-f(y),当x＞1时,有f(x)＞0.

(1)求f(1)的值;

(2)判断f(x)的单调性,并证明你的结论;

(3)若f(4)＝2,解不等式

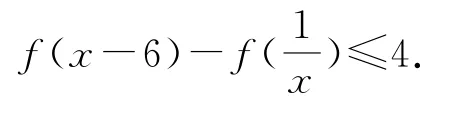
第(1)问用赋值法求f(1);对于第(2)问f(x)的单调性,取自变量大于0的两个点即可判断出f(x)的单调性,证明该结论需构造一个“大”自变量,让它利用当x＞1时,f(x)＞0这一题设条件,故可想到＞1,f)＞0,之后的证明就自然而然了;第(3)问先根据f＝f(x)-f(y)与f(4)＝2猜出函数f(x)＝log2x,得到4＝log216＝f(16),之后用“穿脱”法解决.

(1)在f＝f(x)-f(y)中,令x＝y＝1,得f(1)＝0.

(2)由题意,设0＜x1＜x2,所以＞1,所以＞0,即f(x2)-f(x1)＞0,所以f(x1)＜f(x2),则函数f(x)在(0,＋∞)上单调递增.

解得6＜x≤8,所以原不等式解集为(6,8].

例11定义在R上的函数y＝f(x),f(0)≠0,当x＞0时,f(x)＞1,f(2)＝3,且对任意的a,b∈R,有f(a＋b)＝f(a)f(b).

(1)求f(4)和f(0);

(2)求证:对任意的x∈R,恒有f(x)＞0;

(3)判断f(x)的单调性,并证明你的结论;

(4)不等式f(3-ax)f(ax2-3x)≤9在R上恒成立,求a的取值范围.

第(1)问类比f(a＋b)＝f(a)f(b)用赋值法可求出f(0)和f(4);第(2)问根据当x＞0时,f(x)＞1,只需求证当x＜0时,f(x)＞0即可,通过设x＜0,则-x＞0,再代入f(a＋b)＝f(a)·f(b)即可转化为函数值的关系;第(3)问判断f(x)的单调性,由f(0)与f(4)就可判断出f(x)的单调性,证明需构造一个“大”自变量,让它利用当x＞0 时,f(x)＞1这一题设条件,故可想到x2-x1＞0,之后的证明就顺理成章了;第(4)问根据第(3)问的单调性脱去函数符号“f”,之后蜕变为二次型不等式,再分类讨论求解即可.

(1)在f(a＋b)＝f(a)f(b)中,令a＝b＝2,得f(4)＝9,再令a＝b＝0,结合f(x)≠0,得f(0)＝1.

(2)当x＞0时,f(x)＞1,故设x＜0,则-x＞0,f(-x)＞1在f(a＋b)＝f(a)f(b)中,令a＝x,b＝-x,得1＝f(x)f(-x),即

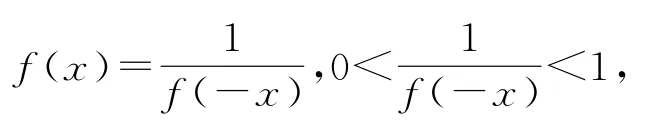
则0＜f(x)＜1,再有f(0)＝1.

综上,对任意的x∈R,恒有f(x)＞0.

(3)由f(0)＝1,f(4)＝9猜测y＝f(x)在R 上为增函数,下面给出证明.

设x1＜x2,则x2-x1＞0,因为

因为x2-x1＞0,所以f(x2-x1)＞1,1-f(x2-x1)＜0.由第(2)问f(x1)＞0,故f(x1)[1-f(x2-x1)]＜0,得f(x1)＜f(x2),所以f(x)在R上为增函数.

(4)因为不等式f(3-ax)f(ax2-3x)≤9在R上恒成立,而f(4)＝9,故f(3-ax)f(ax2-3x)≤f(4),又因为f(a＋b)＝f(a)f(b),所以f(3-ax＋ax2-3x)≤f(4),即

又因为函数f(x)在R 上为增函数,所以ax2-(a＋3)x＋3≤4,即ax2-(a＋3)x-1≤0在R 上恒成立,这是一个二次型不等式,下面分类讨论.

当a＝0时,x≥-在R上不是恒成立,不满足题意;

当a≠0时,不等式为ax2-(a＋3)x-1≤0,这是二次不等式,由ax2-(a＋3)x-1≤0在R上恒成立,必须满足解得-9≤a≤-1,所以原不等式解集为[-9,-1].

第(2)问中,由当x＞0时,f(x)＞1,联想到设x＜0,则-x＞0,f(-x)＞1,进而利用1＝f(x)f(-x),转化得出f(x)＝,体现出解题时等价转化与理性思维的重要性.

从本文可以看出,选择合适的方法策略对解决抽象函数问题能起到十分重要的作用,对于五种方法策略的理解、掌握、应用,则需要在平时的学习中多体会与感悟,这样才能游刃有余地解决此类问题.另外,由于抽象函数问题题设的抽象性,解析式隐而不露,它的解答锻炼了抽象思维能力、逻辑思维能力和等价转化能力,培养了严谨的数学思维,更激发了探索与创新精神.

(完)