城市车辆行驶速度的影响因素研究

冯玲FENG Ling

（南京信息工程大学数学与统计学院，南京 210044）

0 引言

随着居民生活水平和消费水平的提升，交通出行成为家庭中必不可少的部分，对于城市交通系统的探究也更为广泛深入。2020 年，道路交通事故万车死亡人数1.66 人，下降7.8%[1]，虽然呈下降趋势，但是车辆基数总体呈增长趋势，道路安全问题不容小觑[2]。城市交通流的速度、流量和密度的关系是建立城市仿真模型的基础[3]。其中超速是肇事致人死亡较多的违法行为之一，明确建立关于车速的影响因素模型对研究交通安全、交通事故、交通仿真有重要意义。在城市道路上车速高低除了与交通流量密切相关外，还受到道路条件、交通组成、交通管理、驾驶员的习惯等因素影响[4]。

车辆行驶速度对事故发生几率和严重程度均有显著影响[5]，提高行驶安全需要着重研究车速，制动距离和侧翻临界转弯半径都跟行驶车速的平方呈正相关[6]。郑楠等人对典型车型的车速进行累计频率曲线分析发现，大型客车和中型以上载重车在公路上所占比例会对交通情况有较大影响[7]。吴彪等人基于实测数据建立不同区域与车型的车速正态分布模型，说明在施工区路段车速呈现减速趋势[8]。

由于多种因素的综合影响，例如道路因素、交通设施因素、道路环境因素、交通管理因素[9]。使车速研究复杂化，仅靠理论推导的数学模型，难以完整地反映行车速度的实际状况，而交通方面对此建立线性模型来探究影响因素的研究较少，因此文章采用实测的方法，在测量车速的同时，同步测量若干因素，分析并建立数学模型。

1 影响因素分析

文章主要研究车辆行驶速度的影响因素，考虑到中型空载车辆上坡行驶时可能会受到坡度、交通流量及大、中型重载车辆的影响。故选取数据为车速、流量、坡度、重车百分比的实测样本，主要目的是为了分析各变量之间的关系，以及从各数据分析所体现出的交通情况，样本数据中道路宽度为双向两车辆。（表1）

表1 符号说明

由于连续变量较多，依据坡度的数据采用组距分组。图1 为坡度分布，直观地反映出样本中选取坡度为3，3.17，7.3 的数量是一样的，出现频率是6 次，占总样本数量的27.3%。其中坡度为5.9 的测量数据较少，应当多一些测量数据，使交通量和速度的分析更具有普遍性和精确性，一般来说，选取的样本越多，越趋向平均值，则所得分析结果更为精确，更能反映出不同坡度下交通量的情况。

图1 坡度的频数分布

文章对车速y，交通量x2，重车百分率x3采用SPSS 统计分析软件，对试验路段的各参数数据进行处理，进一步了解数据的集中趋势和离散程度，统计结果如表2 所示。

表2 车速、交通量、重车百分比描述统计表

由表2 可看出：车速y 的偏度值-0.021＜0，可以判断为左偏，峰度值-0.737＜0，表明数据的分布比标准正态分布平缓，为平峰分布；交通量x2偏度值-0.105＜0，可以判断为左偏，峰度值-1.331＜0，数据的分布比标准正态分布平缓，为平峰分布，但相较于车速要陡一点；重车百分率的偏度0.881＞0，为右偏，峰度值1.902＞0，表示数据的分布比标准正态分布更陡峭，为尖峰分布。

利用单样本K-S 检验法对车速样本进行正态分布拟合优度检验，计算结果如表3 所示，根据给定的显著性水平α=0.05，由表3 可得，双尾检验概率P 值＞0.05，因此可认为车速样本数据服从正态分布。

表3 车速的正态分布单样本K-S 检验

为了更加直观地分析，分别绘制车速与坡度、交通量、重车百分率的散点图，研究变量间的统计关系以及它们的强弱程度和数据对的可能走向。由图2 不难看出车速与坡度间存在强负相关关系，而很难看出交通量、重车百分比与车速有较明显的相关关系。为了验证其具体的相关性，后文统计计算相关系数分析车速与坡度、交通量、重车百分率的线性关系。

图2 车速、坡度、交通量、重车百分比的散点图

虽然散点图能够直观展现变量之间的统计关系，但并不能精确地表示两者间的相关关系。相关系数以数值的方式精确地反映了两个变量间线性相关的强弱程度。表4 总结了车速与坡度、交通量、重车百分率的相关系数，所提的原假设为：车速与坡度、交通量、重车百分比无线性相关性。

表4 车速与坡度、交通量、重车百分率的相关系数统计表

由表4 可知：车速与坡度的简单相关系数为r=-0.790，表示两变量之间存在强的负的线性相关关系，它的相关系数检验的概率p 近似为0，当显著性水平α 为0.05 时，应拒绝相关系数检验的零假设，认为两总体存在显著的线性相关性，表明坡度对车速的影响较大，坡度越大，车辆行驶越缓慢。与交通量的简单相关系数为r=-0.265，|r|＜0.3，表示两变量之间存在较弱的负相关分析，可以认为两总体不存在显著的线性相关性；车速与重车百分率的简单相关系数为r=0.301，表示两变量之间存在较弱的正线性相关关系，同样依据检验概率，可以认为两总体不存在显著的线性相关性。可以看出，车速变化主要是随坡度变化而变化。

2 车辆行驶速度的经验模型

为了更好地探究分析车速与坡度、交通量、重车比率的关系，建立车速与坡度、交通量、重车比率的关系式。由表5 得出：由于该方程中有多个解释变量，因此参考调整的判定系数。由于调整的判定系数R^2=0.666，判定系数越接近1，拟合优度越高，因此认为拟合优度较高，被解释变量可以被模型解释的部分较多，未能被解释的部分较少。

表5 车速与坡度、交通量、重车比率的模型拟合情况

由表6 得出：被解释变量的总离差平方和为270.673，回归平方和及均方分别为193.2 和64.4，剩余平方和及均方分别为77.472 和4.304，检验统计量的观测值为14.963，对应的概率p 值近似为0。依据该表可进行回归方程的显著性检验。如果显著性水平α 为0.05，由于概率p值小于显著性水平α，应拒绝回归方程显著性检验的零假设，认为各回归系数不同时为0，被解释变量与解释变量全体的线性关系是显著的，可依据车速、重车百分率、交通量、坡度建立线性模型，线性模型关系式如表7 所示：y=33.735±3.453-（1.512±0.356）x1-（1.802±0.757）x2-（0.008±0.065）x3。

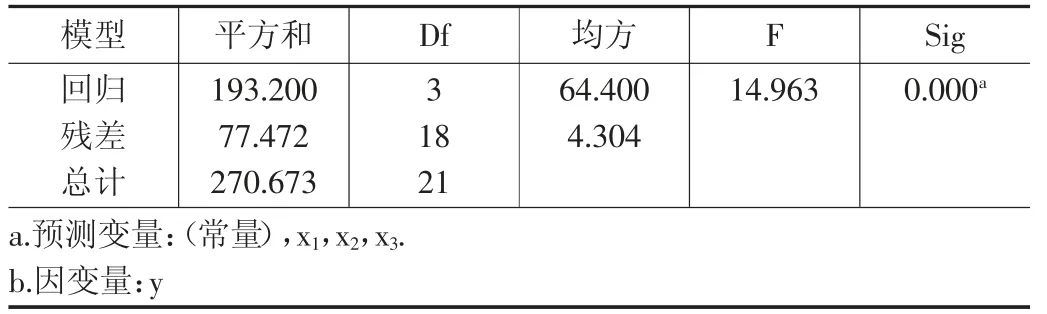
表6 车速与坡度、交通量、重车比率的回归模型

表7 车速与坡度、交通量、重车比率的模型参数及其显著性检验

表9 给出了每个模型中个解释变量的回归系数、回归系数显著性检验的情况。如果显著性水平α 为0.05，由于x3的回归系数显著性检验的概率p 值大于显著性水平α，因此该参数没有显著影响，而x1、x2的概率p 值小于显著性水平α，因此我们将线性关系显著的变量保留在模型中，重新建立线性回归模型如表8 所示：y=33.391±2.186-（1.499±0.229）x1-（1.800±0.737）x2。由于各参数检验的p 值小于显著性水平α，均通过了显著性检验因此模型合理，这说明坡度与交通量对车速的影响存在一定线性模型关系，坡度与交通量越大，车辆行驶速度越缓慢。

表8 车速与坡度、交通量的模型拟合情况

表9 车速与坡度、交通量的模型参数及其显著性检验

研究基于线性模型计算相对的模型值，图3 的横坐标表示样本观测值，纵坐标表示基于模型的对应计算值，可以观察到数值在对角线两边均匀分布，表明基于所求线性模型所计算的车速值能够很好地表示实际观测值。

图3 车速的观测值与模型值比较

3 结论

文章主要研究了车速与坡度、交通量、重车百分率的关系，通过描述性统计、相关分析、线性回归等一系列的分析，探究这些因素对车速的影响，这个研究在交通上有很大的实际意义，对车辆拥堵、交通状况等方面都可以提出一系列的针对性分析，以此想出更好的对策解决当下交通问题。

①以路段实测数据为基础，分析了车辆行驶速度的分布过程和规律并分别建立不同参数的正态分布模型，该模型与实际样本数据拟合较好，为车速特征分析提供有效支持。

②针对坡度、交通流、重车百分比对车速的影响相关分析后，显著影响最高的是坡度，其次是交通流，均呈现负相关关系。重车百分比对车速影响不存在显著相关性。

③探究分析各参数间的数学关系，建立车速与坡度、交通量、重车比率的关系式。确定线性模型y=33.391±2.186-（1.499±0.229）x1-（1.800±0.737）x2，通过调整坡度、交通量来调整车速，以便于缓解车辆拥堵状况，提升行车安全水平。

文章的研究结果表明，坡度、交通流量、重车百分比共同影响了车辆行驶速度，且坡度与交通流量的影响更为显著，该调查结果将为交通管理工作提供重要的参考价值，后续研究可以基于此改善交通拥堵等交通状况，使交通资料调查分析得到更为广泛地发展与应用。