含分布式光伏的有源配电网无功电压控制策略研究
2022-04-22陈志华柯强胡经伟李建坤万姗
陈志华,柯强,胡经伟,李建坤,万姗
(国网黄冈供电公司经济技术研究所,湖北 黄冈 438000)
0 引言
在电力系统中,保持电压的稳定性对于提升供电质量至关重要[1]。由于中压配电系统距用户较近,因此10 kV变电站母线的电压质量起着至关重要的作用[2-3]。通常,在变电站电压无功综合自动控制(voltage quality control,VQC)中,通过结合有载调压变压器(on-load tap changer,OLTC)和电容器组(capacitor banks,CB)实现变电站低压侧和高压侧无功功率的双参数控制[4]。其中,OLTC通过调整抽头位置,保持变电站二次母线的电压恒定,CB则用于补偿无功功率需求,从而降低电压降[5]。针对无功电压控制策略,文献[6-8]针对高渗透率光伏(photovoltaics,PV)的低压配电网的电压特性、运行成本以及线路损耗,提出了兼顾电网运行经济和电压安全的主动电压控制模型,通过双层迭代灾变遗传算法有效提高了多控制变量的解耦性能。文献[9]提出了一种基于动态模式切换的分布式电源电压无功协调控制方案,该方法可在保障实际功率损耗最小化和无功功率储备最大化的前提下,实现电压状况的明显改善。文献[10]针对传统配电网无功电压控制方法无法实现区域协调控制问题,提出了一种用于主动配电网过渡期的自适应双重电压控制方法,有效降低了电网能量损耗,提高电压质量。但上述方法普遍存在设备动作次数大的问题,导致设备成本较高。
目前,九区图控制(nine-zone diagram control,NDC)策略被广泛应用于VQC中,以使电压和无功功率保持在一定的范围内[11]。文献[12]和文献[13]基于NDC控制策略,提出了一种五区图控制和十三区图控制以减少振荡现象,但两种方法中均未解决配电网中的无功功率扰动问题。传统的配电系统常采用NDC控制策略,通过将高压侧无功功率和低压侧电压平面划分成9个区域,从而实现将无功和电压控制在规定的范围内[14]。为了有效降低CB和OLTC误动作次数,NDC控制策略采取多次测量方式,且每两次之间存在一定的延时。
随着分布式光伏电源逐渐接入配电网,其随机性和波动性使得NDC控制策略易导致配电网安全问题无法及时解决,大大降低了设备的使用寿命[5]。鉴于此,本文提出了一种基于九区图和光伏逆变器的无功电压控制策略。首先,基于现有的NDC控制策略,将NDC平面划分为9个区域,根据实时测量的电压和无功功率值确定OLTC和CB控制策略,同时通过构建的时间序列控制结构,减少了传统设备的动作次数;其次,利用Q-U曲线对多个调节装置进行建模,提出了一种计算光伏输出和跟踪电压值的算法,计算光伏逆变器控制(PV inverter control,PVC)范围内的最优值,避免了难以找到最优解的情况。最后,通过Matlab进行了多种案例下的控制仿真,验证了所提控制策略的有效性。
1 含光伏的配电网无功功率控制架构
目前,九区图控制广泛应用于VQC控制中,能够将变电站的低侧电压和高侧无功功率保持在可控范围内[16-17]。图1所示为九区图控制原理图。由图可知,协调平面分别由水平轴上的无功功率和垂直轴上的电压绘制。当无功功率或电压处于异常区域时,采用适当的控制方法将其保持在正常区域。图1中区域9为正常区域,因此不采取任何控制措施。
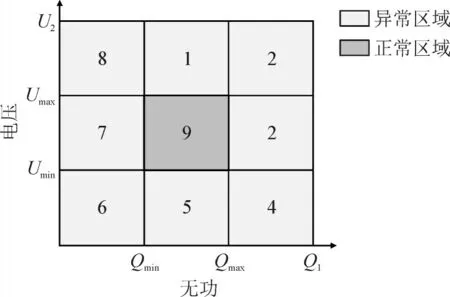
图1 九区图控制Fig.1 Control of nine-zone diagram
本文提出的基于NDC和PVC的无功电压控制策略控制方法,强调提高低压侧电压U2质量,使高压侧无功功率Q1满足要求,同时减少OLTC和CB操作次数。图2所示为所提出的控制架构,其中NDC系统与OLTC和CB具有通信链路,并在VQC系统中应用光伏逆变器控制与所有PV进行通信。
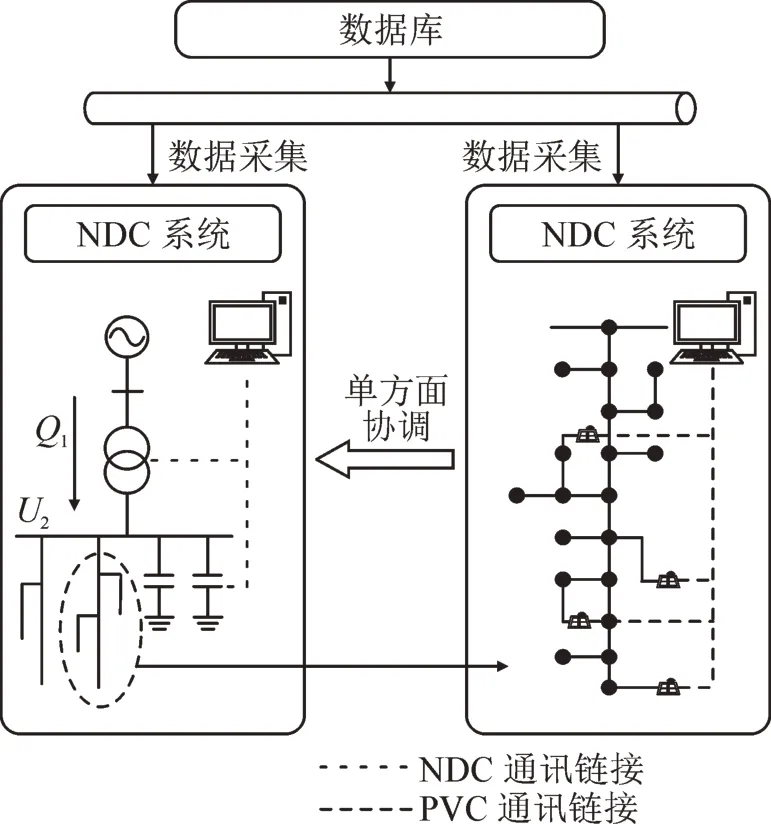
图2 无功电压控制策略架构Fig.2 Structure of reactive voltage control strategy
当电压或无功功率落入非理想区域时,NDC将存在时间延迟,考虑到传统设备无法解决时间延迟问题,PVC将被优先运行。在最优情况下,PV有可能在不运行OLTC和CB的情况下将电压和无功功率带入区域9。
图3为基于NDC和PVC的无功电压控制策略的时间协同图,从图3可以看出PVC和NDC在时域上为单向合作关系。该策略由两个控制层组成。其中,一个控制层位于周期T中的nT+t1处,为PVC层;另一层位于周期T中的nT+t2处,为NDC层。

图3 基于NDC和PVC控制策略的时间协同Fig.3 Time coordination based on NDC and PVC control strategies
通常,PVC层由参考值计算和参考值跟踪两部分组成。首先,利用最新的最优低压侧电压值调整无功功率及其他测量数据,PVC确定其最佳电压参考,以满足控制层结束时,即(n+1)T时刻的目标。其次,将无功功率分配给每个PV,以跟踪设定点命令。PVC控制后,低压侧和高压侧无功功率更新为(U2(nT+t2)和Q1(nT+t2))。
OLTC和CB在NDC控制层的控制作用由变量U2((nT+t2)和Q1(nT+t2))决定。通过选择NDC层考虑光伏控制作用对OLTC和CB操作次数的影响。最后,用新测量的OLTC和CB状态更新下一个周期的数据。
2 含光伏的配电网无功电压控制模型构建
2.1 系统描述与分析
图4所示为典型含光伏配电网的等效电路。其中:UG为发电机电压参考值;U1为变电站高压侧电压值;U2为变电站低压侧电压值;P1+Q1为变电站高压侧功率;PL+jQL表示具有滞后功率因数的聚合负载;PPV+jQPV表示馈线上PV的总注入有功和无功功率;jQC表示CB的注入无功功率;RG+jXG表示输电线路阻抗之和;RT+jXT表示变压器阻抗。忽略线路和变压器的并联支路,总电阻和电抗公式为
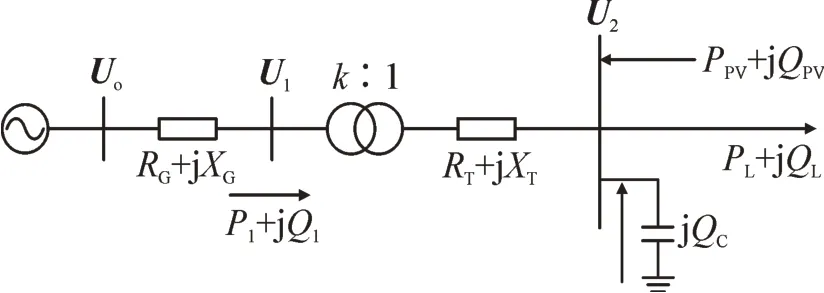
图4 典型含光伏配电网的等效电路Fig.4 Typical equivalent circuit of typical photovoltaic distribution network
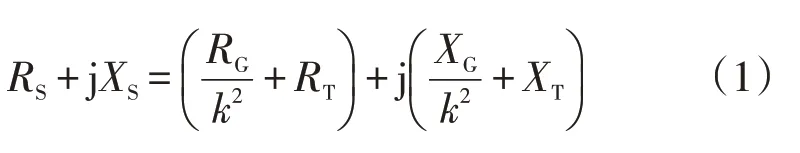
式中,k为OLTC的匝数比。
由于发电机的模型为恒压源UG,因此电压方程公式为
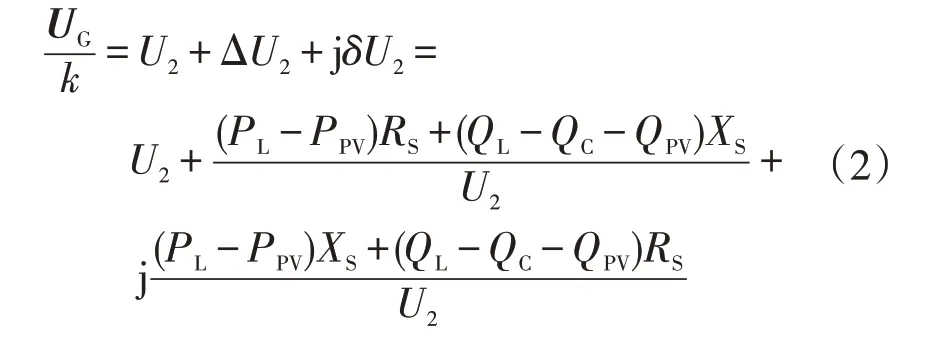
式中:ΔU2为电压降实部;jδU2为电压降虚部。
在配电系统中电压降的虚部可以忽略,因此公式(2)可以替换成公式为

当PV或CB的输出增加时,QL-QC-QPV可能会变小甚至为负,从而减小电压降。因此,PV和CB的无功功率会引起电压变化。
根据电压U2,高端无功功率公式为
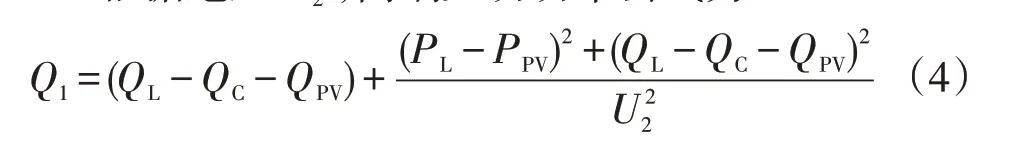
由式(4)可知,Q1与PV和CB的无功功率之间存在负相关。将式(3)取导数可得公式为
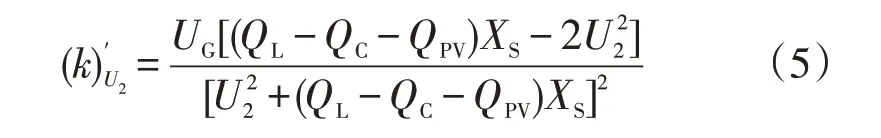
由式中可知,U2是相对于k的单调递减函数,因此Q1和k之间存在负相关。
2.2 OLTC模型构建
OLTC抽头位置的调整步骤为{-4、-3、-2、-1、0、1、2、3、4},其提供相对较少的电压校正,通常为标称电压的1.25%。
OLTC的抽头位置和匝数比公式为
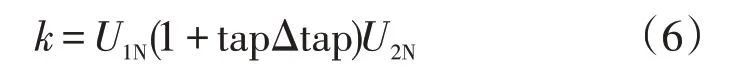
式中:U1和U2为一次绕组和二次绕组的额定电压;tap为有载分接开关的抽头位置;Δtap为两个抽头位置之间的最小电压校正,即0.012 5。通常,抽头位置的调整对系统阻抗RS+jXS影响不大,为了描述OLTC对无功功率和电压的影响,采用如下简化计算。
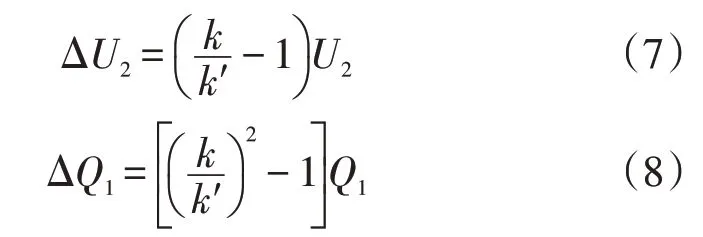
式中,k和k′分别为调整前后的匝数比。考虑到连续抽头位置调整之间存在间隔,因此调整前的抽头位置与一个周期内调整后的抽头位置相差一个位置。
2.3 CB与PV模型构建
通过灵敏度分析CB无功功率控制,使系统在其工作点附近呈现线性化,从而得到最优变量与无功功率变化间的关系。
低压侧和高压侧无功功率的变化计算公式为
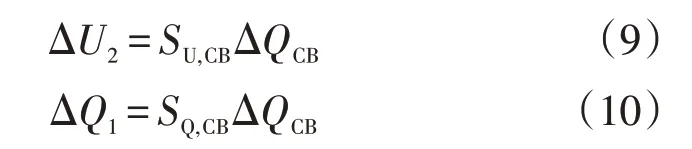
式中:SU,CB为与无功功率相关联的低压侧电压的灵敏度值;SQ,CB为与无功功率相关联的高压侧无功功率的灵敏度值;ΔQCB为无功功率变化率。
光伏的无功功率通常是可控的,但却受有功功率、容量和功率因数的影响。因此,控制器不能超过产生的功率,其光伏发电可产生的最大无功功率如下式所示。
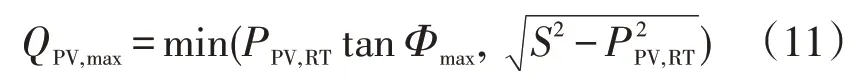
式中:S为PV的容量;Φmax为最大允许功率角;PPV,RT为PV的实时有功功率。
为了充分利用最大无功功率的能力,需要根据实际的有功发电量更新最大无功功率。假设电容性无功功率为正,电感性无功功率为负,调整量可以描述为

式中:QPV,RT为PV的实时无功功率;Umin和Umax分别为电压在九区平面的上限和下限。
电压和无功功率的变化为
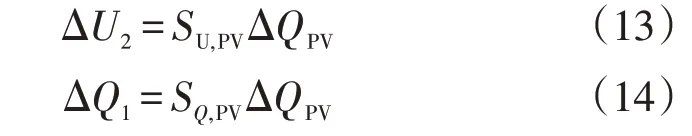
式中:SU,PV为低压侧电压对PV无功功率的灵敏度值;SQ,PV为高压侧无功功率对PV的无功功率的灵敏度值;ΔQPV为光伏的变化无功功率。
3 PVC控制策略
3.1 电压参考值计算
PVC由参考值计算和参考值跟踪组成,因此可选择参考值作为所有PV的母线电压或总无功功率。若使用电压设定值,当连接到PV的任一通信出现问题,PVC仍可以跟踪预定义值。
考虑到变电站的运行效率和电压分布,将传统设备在NDC范围内的最小总运行量与控制范围内的最小电压偏差相结合,构建的目标函数为

式中:ΔTtap和ΔNCB分别为OLTC和CB的操作次数;U2((n+1)T)为(n+1)T时刻的预测总线电压大小的集合。
在该多目标优化问题中,由于后一个目标维持电压稳定需要较高的成本,因此前一个目标比后一个目标具有更高的优先级。
其约束条件为

式中:∑ΔQPV为PV无功输出的总变化;Umin和Umax为电压的上限和下限;Qmin和Qmax为9区平面中的无功功率上下限;(n+1)T为一次性控制周期的终点。
在此约束中引入电压和无功功率限制,以避免在下一个周期中OLTC和CB的操作。由于NDC有多种情况,因此难以用现有方法有效解决优化问题,使得难以将离散设备的数量表示为精确的数学公式。可通过采用Q-U曲线的方法解决优化问题。根据式(13)和(14)可知,低侧电压和高侧无功功率随PV无功功率变化而改变,馈线上的总PV等于变电站母线上的PV。因此,PV的Q-U曲线为
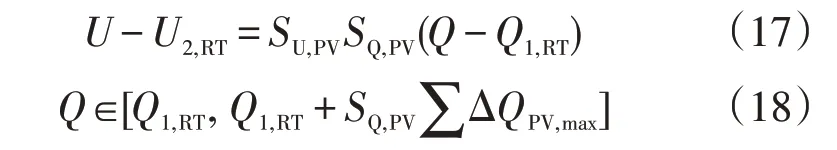
式中:SU,PV和SQ,PV分别为相对于母线等效PV的低侧电压和高端无功的灵敏度值。
式(18)中,Q的范围表示PV调节电压和无功功率的最大容量。由上式可知,PV的Q-U曲线表明了当PV电流值从当前值变为最大值时电压和无功功率的位置变化情况,沿曲线的任何点都可以通过PV获得。
图5所示为PVC的典型案例,电压和无功功率的位置受到限制。最上斜线是可通过式(17)和(18)计算的PV的Q-U曲线。
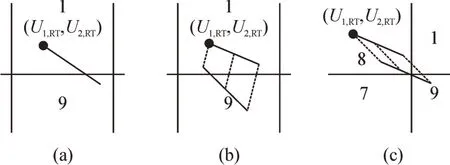
图5 PVC的典型案例Fig.5 Typical case of PVC
考虑到NDC中PV的容量和控制策略不同,将其主要分为以下几种情况:
1)若PV的Q-U曲线通过区域9,如图5(a)所示,则表示使用PV的无功功率可以优化电压性能或消除干扰。取曲线上的一个点,并根据式(15)中的后一个目标函数和式(16)中的约束对其进行计算,作为电压参考值。
2)若PV的Q-U曲线未通过区域9,则表示必须结合PVC和NDC来调整曲线,即称为调整后的Q-U曲线。当曲线经过9个区域平面中OLTC的第1个操作区域时,应在nT+t2处的OLTC操作调整Q-U曲线。如图5(b)所示,虚线为无功功率和电压的变化曲线,抽头从不同的初始点开始调整。将式(7)和式(8)代入式(17),可获得调整后的Q-U曲线,其最下边曲线表示为

3)若Q-U曲线未经过区域9,而经过CB组成的第1操作区域,则考虑通过CB操作调整Q-U曲线。如图5(c)所示,虚线是无功功率和电压的变化曲线,其中一组CB从不同的初始点被切断。将式(9)和式(10)代入式(17),可获得调整后的Q-U曲线,其最下边曲线表示为
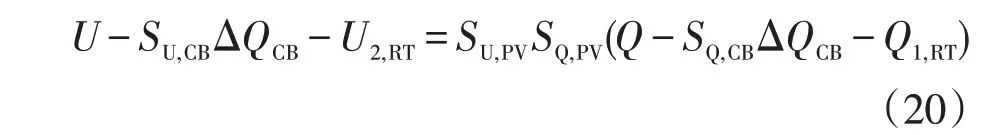
在第2、3情况中,最下边曲线是在PV和传统设备操作下调整后的Q-U曲线。若调整后的Q-U曲线通过区域9,则根据式(15)中的后一个目标函数,及式(16)中的约束条件计算电压参考值。否则,电压和无功功率不能在一个周期内满足要求,并将其设置为初始电压值U2,RT。
3.2 电压参考值跟踪
电压参考值跟踪用于将总无功功率分配给PV系统,以跟踪电压设置点。图6所示为电压基准值跟踪流程图。
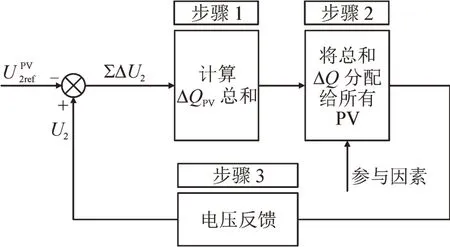
图6 电压基准值跟踪流程图Fig.6 Tracking flowchart of voltage reference value
由图6可知,在步骤1中,PVC根据低侧母线上的灵敏度SU,PV,将低侧母线电压的偏置转换为PV的总无功功率需求,其计算公式为

在步骤2中,将ΔQPV的总和分配给分布式电网中连接的所有PV单元。由于灵敏度是离线的,且在无功功率传输期间存在损耗,因此在步骤3中采用电压反馈消除偏差。通过比较电压参考值和实时反馈值,修改总无功功率。
4 仿真验证与分析
4.1 网络描述
为了验证所提出的控制策略的有效性,利用修改后的IEEE 33节点系统进行测试,见图7。由图7可知,在该配电网中,具有用于电压和无功功率调节的基本配电系统设备。在节点1和节点2之间存在OLTC,并具有17个分接头抽头,每个抽头的调节率为1.25%,节点2连接了2 400 kvar的可切换CB,其光伏装置的基本参数见表1。

表1 PV的基本参数Table 1 Basic parameters of PV
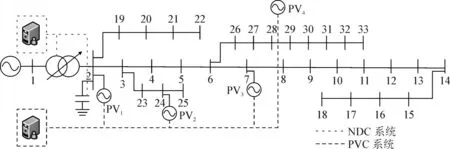
图7 修改后的IEEE 33节点系统的结构Fig.7 Structure of IEEE 33-node system after modification
图8所示为预测的每日总负荷曲线和总PV功率曲线。由图8可知,PV输出在14:00达到最大值,负载在17:00达到峰值。后续仿真过程中将选择这2个时刻,以验证所提出控制策略的电压和无功功率调节性能。
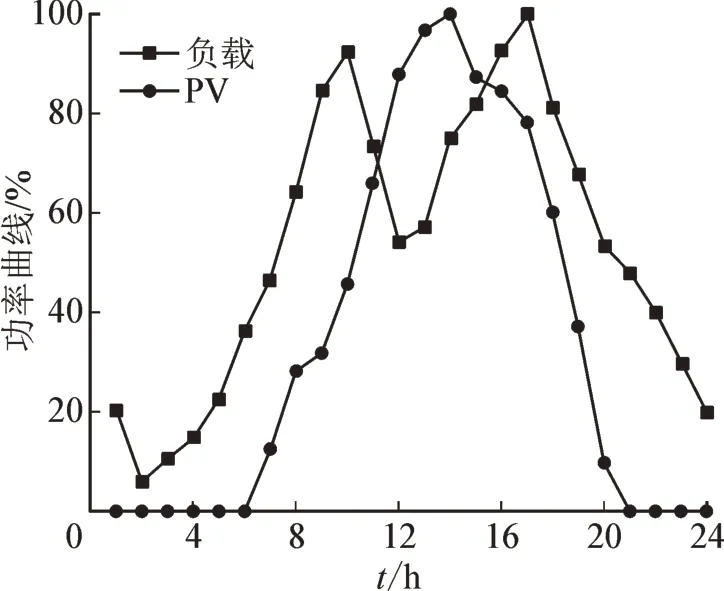
图8 每日总负荷预测曲线和总PV预测曲线Fig.8 Daily total load prediction curve and total PV prediction curve
使用Matlab/Simulink进行配电网和控制算法仿真建模。设定系统基准容量为100 MVA,低侧电压上限Umax和下限Umin为1.05 p.u.和0.95 p.u.,参考电压为1.03。此次仿真中不允许高端无功功率反转,因此初级无功功率下限Qmin为0,高端变电站的功率因数PF不小于0.8。因此,无功功率性能被PF性能代替,以反映仿真中的调节效果。正常模式下,带有有功功率PPV的PV的最小功率因数为0.95,紧急模式下为0.9。为了建立经济的评估指标,OLTC的调整成本预估为$6,每个定时单位一个CB组的交换成本预估为$3,光伏的无功电价估计为0.1$/Mvar。仿真中,为了反映不同设备的响应时间,在10 s时执行PVC层,在20 s时开始NDC层。
4.2 性能比较
为了验证所提策略的电压和无功功率调节能力,将PV有功功率和负载变化作为干扰,使电压或无功功率在不同程度上达到极限,对3种不同的案例进行了仿真。图9所示为9个区域平面中3种案例的低侧电压和高侧无功功率位置。其中,U2为低压侧电压,Q1为变电站的高压侧无功功率。案例1中,无功功率满足要求,但电压达到上限;案例2中,电压和无功功率均达到极限;案例3中,电压和无功功率在可接受范围内。
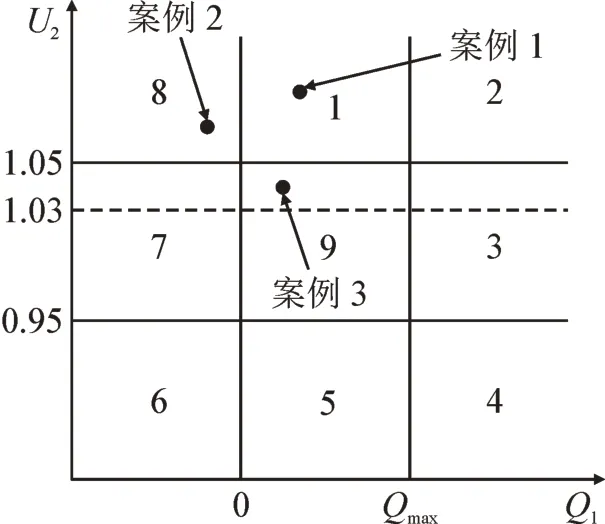
图9 9个区域平面中3个案例的位置Fig.9 Location of three cases in nine regional planes
为比较和分析每种情况下不同控制的性能,选择以下4种控制策略进行仿真验证:
策略1:本文控制策略。
策略2:采用NDC策略。
策略3:不采用控制策略。
策略4:PVC和NDC策略分别运行。
4.2.1 案例1
假设天气在14:00从多云转晴,并且在3 s时PV的有功功率突然增加,则电压将增加并超过上限。如图9所示,电压和无功功率进入区域1,在该区域OLTC将使用原始NDC策略调整抽头降压,在系统中执行了前3种策略。图10所示为案例1的仿真过程。其中,图10(a)和图10(b)显示了采用不同策略节点2处和节点1处的电压校正。
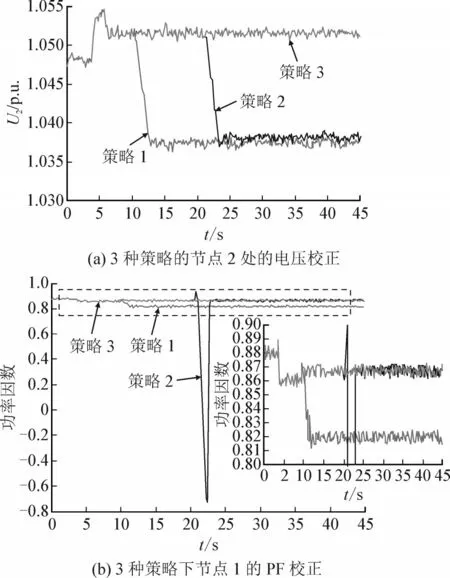
图10 案例1的仿真Fig.10 Simulation of case 1
策略1中,在第10 s位置时,采用了本文的控制策略,由于PV具有足够的无功功率容量,因此避免了OLTC在NDC范围内的运行,这也是在案例1中未采用策略4的原因。在12 s后消除了超限电压,电压为1.037 5 p.u.。图11所示为采用策略1的4个PV的无功输出变化。
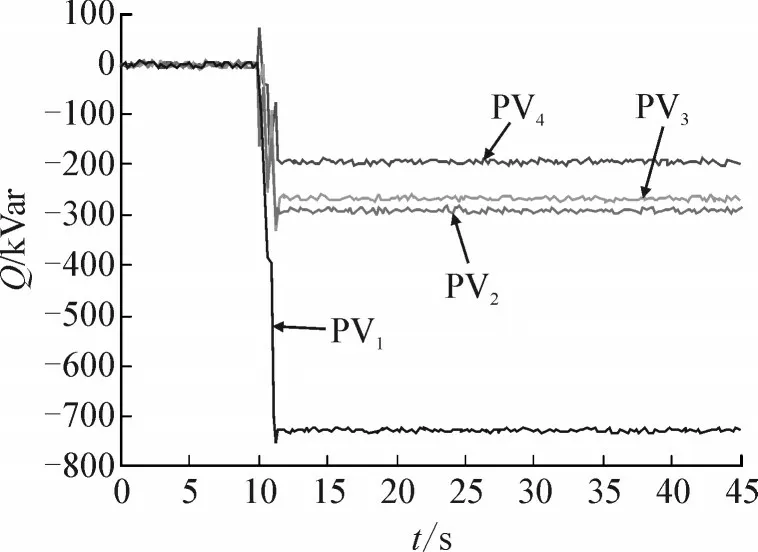
图11 案例1中采用策略1的PV无功输出Fig.11 PV reactive power output using strategy 1 in case 1
由图可知,当PV的无功功率耗尽时,该电压未达到参考值。如图10(b)所示,由于PV产生感应无功功率,因此PF从0.86降低到0.81。
策略2中,在第20 s处使用NDC,OLTC将抽头位置从-1更改为0。电压从1.052 0跃升至1.037 8,超限问题在24 s内得到解决。在OLTC操作前后,节点1的PF值变化较小,但在抽头过渡期间存在较大的中断。表2所示为3种策略的调节结果。由表2可知,采用策略1和策略2,电压和无功功率能够在合理范围内运行。尽管策略1的无功功率略差于策略2,但相关问题已通过策略1得以解决。另外,策略1减少了OLTC的运行,从而降低了配电网的运行成本。
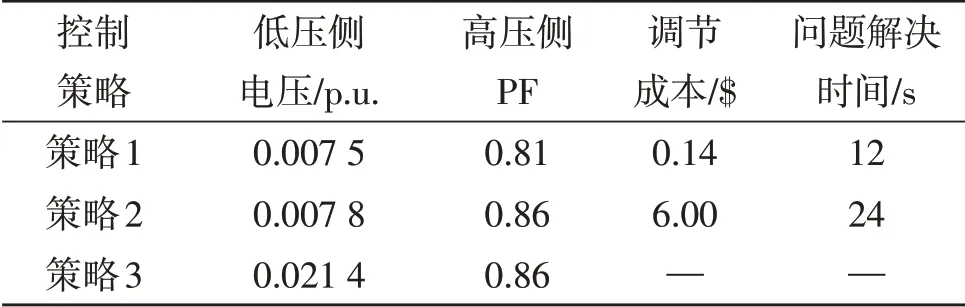
表2 案例1的3种策略的调节结果Table 2 Adjustment results of the three strategies of case 1
4.2.2 案例2
达到高峰期后,负载在17:00开始减少。此时负载从高峰时段开始减少,电压急剧上升,无功功率逐渐下降。如图9所示低侧电压和高侧无功功率位于区域8中,在该区域中,1组CB将仅通过原始NDC进行切换。因此,系统采用4种策略进行仿真。图12所示为案例2的仿真过程。

图12 案例2的仿真过程Fig.12 Simulation process of case 2
策略1中,PVC系统无法在9区提高电压和无功功率。在12 s时的PVC操作中,该问题得到了轻微缓解,并且在23 s时,1组CB被切断,电压恢复到1.029 9。如图12(b)所示,由于PV和CB无功功率的影响,PF更改为0.99。因此,PV不必提供所有无功功率,通过PVC和NDC配合,电压即可达到参考值。其中,使用策略1的4个PV的无功功率输出变化见图13。
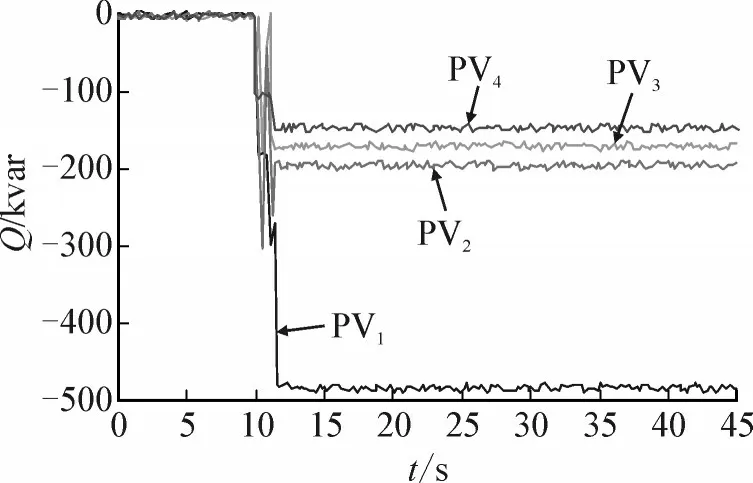
图13 案例2中策略1的PV无功功率输出Fig.13 PV reactive power output of strategy 1 in case 2
策略2中,切断1组断路器,并在24 s处消除风险,低压侧电压达到1.037 1 p.u.,高端PF变为0.99。由于CB的离散性,电压无法达到最佳效果。
表3所示为案例2的调节结果。比较3种不同策略的效果,将电压和无功功率同时控制在可接受范围内。由于PVC的连续性和协同性可知,策略1的电压性能优于策略2及策略4的电压性能。因此,通过充分利用光伏特性,采用本文控制策略可以实现电压的无偏差调节。
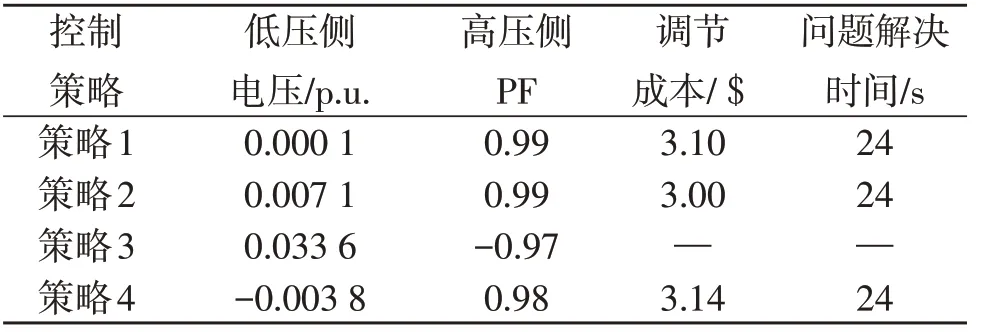
表3 案例2的4种策略的调节结果Table 3 Adjustment results of four strategies of case 2
4.2.3 案例3
案例3中电压和无功功率均在限制范围内,但服务入口处的电压未达到最佳值。由于电压和无功功率满足要求,因此在NDC中仅应用了策略1。案例3的仿真结果见图14。

图14 案例3中策略1的仿真过程Fig.14 Simulation process of strategy 1 in case 3
由图14可知,使用策略1在10 s处进行电压优化具有良好的可行性。在使用策略1进行优化前后,系统中从节点2到节点33的电压曲线如图14(a)所示。图14(c)展示了使用策略1的PV无功输出。由图可知,无功功率的最大变化发生在节点2上的PV中,该节点具有最适当的已调节无功功率容量。
5 结语
针对传统配电系统电压和无功功率扰动的问题,提出了一种基于九区图和光伏逆变器控制的电压和无功功率控制策略,并通过分析与实验得出以下结论:
1)该策略能够将具有PV无功功率的PVC与NDC进行协同工作,同时不改变VQC系统中原有的NDC,具有良好的工程推广价值;
2)利用Q-U曲线对多个调节装置进行建模,计算PVC控制范围内的最优值,提升最优解计算效率;
3)当电压和无功功率在正常范围内时,可进一步校正电压,防止配电系统出现扰动。
