基于滤波协同状态转移的动态无功优化方法
2022-04-22王正国金良峰孙钢彭双武
王正国,金良峰,孙钢,彭双武
(1.国网浙江省电力有限公司电力科学研究院,杭州 310004;2.浙江华云信息科技有限公司,杭州 310000)
0 引言
动态无功优化(DRPO)对电力系统的安全与经济运行具有十分重要的意义[1-2]。在满足一定的约束条件下,DRPO不仅可以减少有功功率传输过程中的功率损耗,还可使所有母线电压保持在安全运行范围内。但由于受到控制设备动作数的约束,使得DRPO成为了一个大规模的多周期混合整数非线性规划问题[3-7],而如何有效处理离散变量和无功功率控制设备的动作数约束便成为了解决DRPO问题的关键所在[8-10]。
针对动态无功优化算法,研究学者进行了大量研究。文献[11-12]提出了一种基于精英策略、帕累托控制排序和拥挤距离排序的多目标萤火虫算法,以优化无功功率控制的数学模型,解决最佳无功调度问题。但其目标为静态无功优化,而在现实环境中,因为负载会随时间变化,所以需要实时调整控制设备,以满足电力系统的需求。针对这一问题,文献[13-14]提出了一种基于多种群蚁群算法的优化解决方案,该方案建立了多目标动态DRPO模型,确保在不同状态下找到全局最优解,但算法复杂度较高。文献[15-16]提出了一种基于无功设备运行极限与电网安全性的混合整数非线性规划模型,运用该模型可快速获得最优解,却降低了经济效率。
针对目前方法无法兼顾算法复杂度和经济性的问题,本文提出了基于滤波协同状态转移的动态无功优化方法。本文首先对DRPO问题进行数学建模,建立双目标DRPO模型。然后将滤波协同状态转移算法应用到DRPO问题上,该算法通过滤波技术确定优化方案,并通过双种群并行搜索技术,确定模型整体最优解,保证了解决DRPO问题的速度和准确性[17]。最后,利用IEEE14系统和东莞某53节点配电系统仿真验证了所提方法的有效性。
1 双目标DRPO的数学建模
电力系统动态无功控制不仅要保证当前运行状态的安全性和经济性,还要满足无功控制设备全天的动作次数限制[18-25]。为此,本文设置双目标DRPO模型。第1目标函数旨在最大程度地减小系统网络损耗,以保证系统当前的运行状态最优;第2目标函数旨在最大程度地减少无功控制设备(本文主要指电容器与有载调压变压器)的动作次数,以保证系统安全稳定运行。双目标DRPO的模型关系见图1,两个目标函数同时分别朝着不同的功能方向进行并行搜索,每次迭代完成后进行最优解交换,即整合双方的最优解集,根据各自的约束进行优胜劣汰,将得到的结果作为各自下一次迭代的优化初值,直到到达指定迭代次数,将结果输出出来。如此反复,可以保证系统网络损耗与无功控制设备的动作次数达到相对较小的水平。

图1 双目标DRPO模型图Fig.1 Diagram of dual-target DRPO model
1.1 第1目标函数和约束
1)目标函数。
第1目标函数旨在最大程度地减小系统网络损耗,其计算公式为
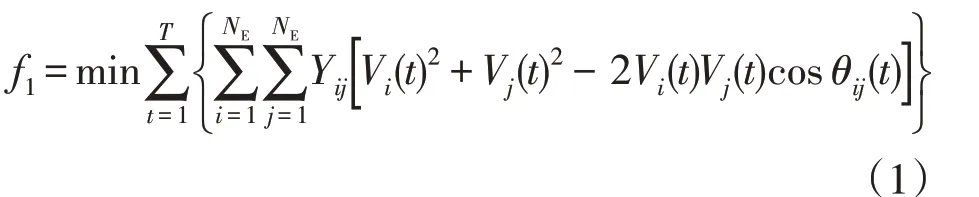
式中:f1为第1目标函数;T为1天中的时间(T=1,2,…,24);NE为网络节点数量;Yij为导纳矩阵第i行第j列的元素;Vi(t)和Vj(t)分别为t时刻母线i和母线j的电压;θij(t)为t时刻母线i和母线j之间的电压相角差。
2)等式约束。
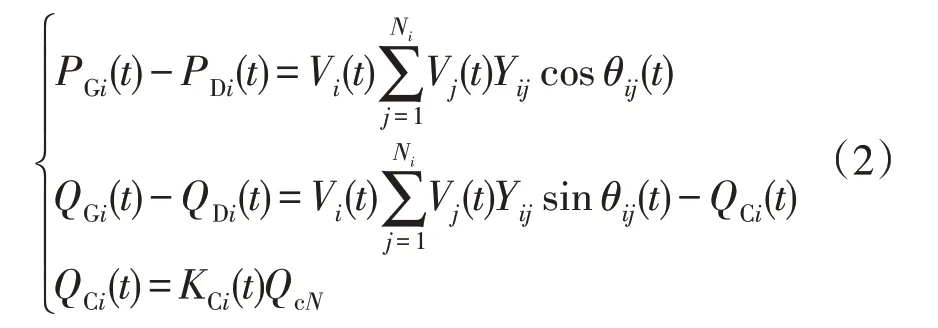
式中:PGi(t)和QGi(t)分别为t时刻母线i发出的有功功率与无功功率;PDj(t)与QDj(t)分别为t时刻母线i上的有功负荷与无功负荷;Ni为与母线i相邻的线路总数(包括母线i);QCi(t)为t时刻母线i上电容器发出的无功功率;QcN为单组电容器的容量;KCi(t)为t时刻母线i上发出无功功率的电容器的数量。
3)不等式约束。
如式(3)所示,必须将所有平衡节点的输出功率限制在各自的上下限内。
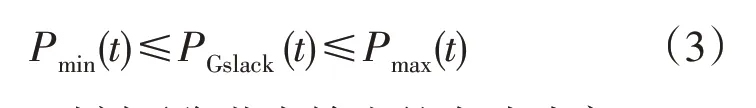
式中,PGslack为t时刻平衡节点输出的有功功率。
除此之外,如式(4)所示,发电机的无功功率、电容器的投切次数与有载调压变压器分接头的动作次数都必须限制在各自的上下限内。

式中:QGi(t)为发电机的无功功率;kCi(t)为电容器的投切次数;kTi(t)为有载调压变压器分接头的动作次数,三者均为待优化控制变量。
1.2 第2目标函数和约束
1)目标函数。
第2目标函数旨在最大程度地减少无功控制设备的动作次数,以保证系统安全稳定运行。
其计算公式为
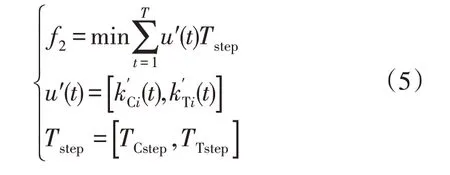
式中:f2为第2目标函数;u′(t)为离散性控制变量;Tstep为无功控制设备的动作次数;TCstep为电容器的动作次数;TTstep为有载调压变压器分接头的动作次数。
2)不等式约束。
如式(6)所示,控制变量必须在其上下限范围内进行调整。
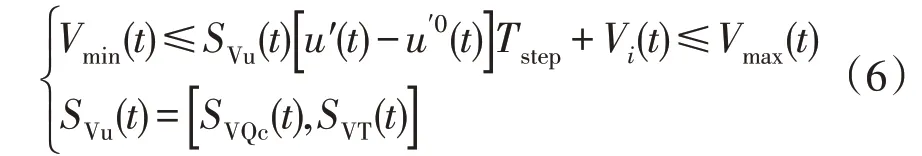
式中:SVu(t)为t时刻控制变量的母线电压灵敏度矩阵;SVQc(t)为带电容器的母线电压;SVT(t)为带变压器的母线电压。
一天内无功控制设备的动作次数约束公式为

式中:kCimax为kCi(t)的最大值;kTimax为kTi(t)的最大值。
2 状态转移算法与滤波技术
2.1 基本状态转移算法
基本状态转移算法是一种智能型随机性全局优化算法,主要针对于无约束连续优化问题。基本思想是将优化问题的一个解当作一个状态,将解的产生和更新看作是状态转移过程。因此,优化问题的求解过程可以看作是状态转移的过程,其表达式为
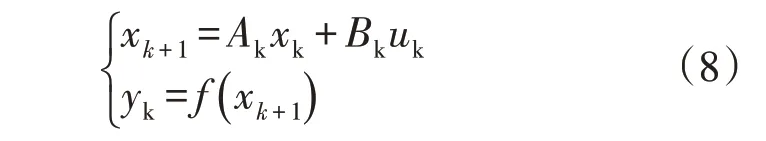
式中:xk为某一状态,对应一个优化解决方案;Ak、Bk为状态转移矩阵;uk为状态xk及其历史状态的函数;yk为在xk点的适应值;f(xk)为目标函数。
状态转移算法共有4个运算符,其详细信息如下所示:
1)旋转变换。
旋转变化(rotation transformation,RT),其表达式为
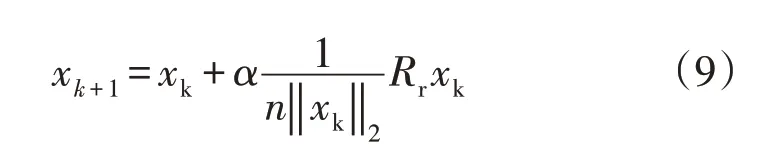
式中:α>0为旋转因子;Rr为一个其元素取值在[-1,1]之间均匀分布的随机矩阵;‖xk‖2为xk的二范数。旋转变换具有在以α为半径的超球内进行搜索的功能。
2)平移变换。
平移变换(translation transformation,TT)具有从起始点xk,沿x k-1到xk的直线搜索的功能,且最大搜索长度为β,其表达式为
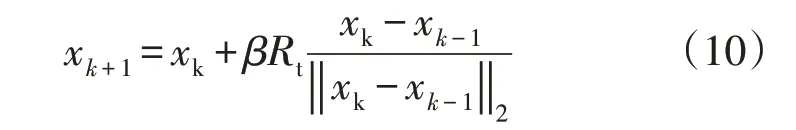
式中:β>0为平移因子;Rt是一个其元素取值在[0,1]之间均匀分布的随机数。
3)伸缩变换。
伸缩变换(expansion transformation,ET)具有将x k中的元素扩展到[-∞,+∞]范围的功能,可以在整个空间中搜索,其表达式为

式中:γ>0为伸缩因子;Re为一个其非零元素取值服从高斯分布的随机对角矩阵。
4)坐标变换。
坐标变换(axesiontransformation,AT)具有沿坐标轴搜索并加强一维搜索的功能,其表达式为
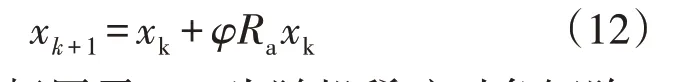
式中:φ>0为坐标因子;Ra为随机稀疏对角矩阵,其元素服从高斯分布,并且只在某一随机位置有非0元素。
状态转移算法的基本流程图见图2,其中RT表示旋转变换,TT表示平移变换,ET表示伸缩变换,AT表示坐标变换。

图2 状态转移算法流程图Fig.2 Flow chart of state transition algorithm
其中αmin一般选择为1×10-4。状态转移算法首先初始化生成初始解,然后通过状态转移算子生成新的可行解集,从中选取令目标函数值更小的解,然后再次通过状态转移算子生成新的可行解集,如此循环上述过程,直到满足条件或者达到迭代次数。状态转移算法中采用了交替轮换的机制使用各种搜索算子,即RT、ET和AT轮换进行,并且在分别使用RT、ET和AT后调用了TT。采用的交替轮换机制是为了适应不同结构类型优化问题的需要,他的一大好处是在未达到全局最优解邻域时,避免浪费过多的时间进行局部搜索,增强搜索过程的活跃性。
2.2 滤波技术
目前已有研究表明,滤波技术可用于求解约束优化问题。其表达式为
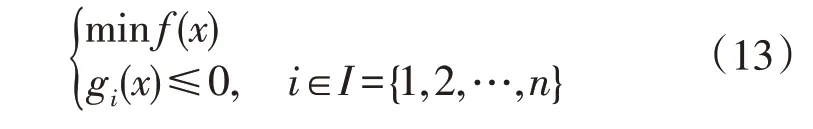
式中:f(x)为目标函数;gi(x)为约束函数;I为一组约束条件。
满足所有约束条件的点称为可行点,如式(14)所示,所有可行点的集合称为可行域,用X来表示。
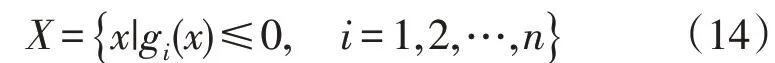
滤波技术的原理如下所示:
1)约束符合度函数f与约束违反度函数h构成滤波器(f,h),其中
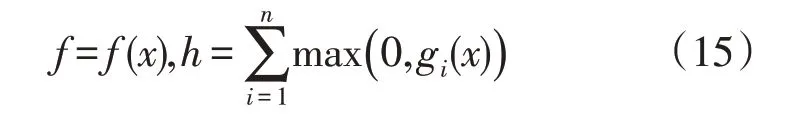
2)滤波器(fi,hi)对应于点xi,滤波器(fj,hj)对应于该点x j。当f i≤f j且h i≤h j时,点xi对应的解决方案要优于点x j对应的解决方案。
3)F为滤波器集,其中所有的滤波器互不相影响。
4)如果xk为新生成的点,则将其滤波器(fk,hk)添加到滤波器集F中,并与滤波器集中原有的滤波器作比较,若滤波器(fk,hk)优于原始滤波器中的某一个滤波器,则接受(fk,hk),并删除对应的旧滤波器,即滤波器集可以决定是否接受新的解决方案。
3 基于FCSTA的双目标DRPO算法
3.1 状态转移算法与滤波技术的关系
前文介绍了基本状态转移算法的原理,然而基本状态转移算法是针对无约束连续优化问题的,并不能求解约束优化问题,因此需要结合滤波技术。通过将约束违反度h和约束符合度函数f相结合形成的滤波器作为状态转移算法的目标函数,就可以实现将约束优化问题转化为无约束优化问题,然后就可以采用基本状态转移算法进行优化求解。状态转移与滤波技术结合的算法称为滤波协同状态转移算法。
3.2 滤波协同状态转移算法
为了解决动态无功优化问题,本文提出了一种基于滤波协同状态转移(FCSTA)的双目标DRPO算法。该算法通过滤波技术确定优化方案,并通过双种群并行搜索技术,确定模型整体最优解,保证了解决DRPO问题的速度和准确性。
假设有两个种群S1与S2,S1与S2中元素的个数共为N,迭代次数为T,最优解为x=[x1,x2],其对应的滤波器为(f1,h1)与(f2,h2),滤波器集分别为F1与F2,且F1与F2的数目分别为N1和N2。
图3所示为FCSTA的基本流程图。

图3 FCSTA基本流程图Fig.3 Basic flow chart of FCSTA
1)初始化。
将S1与S2两个种群中的所有元素以及两个滤波器集初始化,并设置迭代次数为T。
2)生成初始状态。
在S1与S2中各元素的最大值与最小值内随机生成初始解向量。
3)生成初始滤波器集。
将初始解向量中关于种群S1的解所对应的滤波都添加到滤波器集F1中。同理,将初始解向量中关于种群S2的解所对应的滤波器都添加到滤波器集F2中,形成初始滤波器集。
4)进行4种状态转移运算。
种群S1与S2中的所有元素均进行RT、TT、ET和AT 4项运算。
5)更新滤波器集。
完成4项操作后,计算目标函数值。假设滤波器(fi,hi)为新滤波器,(fj,hj)为滤波器集中的旧滤波器,当f i≤f j且h i≤h j,则新的滤波器(f j,hj)可以被滤波器集接受,旧滤波器(f j,hj)将被删除,实现滤波器集的更新。
6)交换最优解。
在迭代过程中,两个种群交换其最优解,并更新滤波器集。
7)计算新滤波器的数量。
设新滤波器的数量为m1、m2,在整个处理过程中,滤波器集中滤波器的数量必须保持不变。以S1为例:
若m1=N1,则进入下一次迭代;
若m1<N1,则随机添加(N1-m1)个新滤波器到滤波器集中,以保持数量不变;
若m1>N1,则根据目标函数f,对所有滤波器进行排序,选择N1个最佳滤波器组成新的滤波集。
8)终止条件检查。
如果迭代次数等于设定值T,则算法中止,否则,算法将返回到步骤2继续进行新一轮的迭代。
3.3 适用于DRPO问题的FCSTA
利用种群S1来替代第1个目标函数和约束条件,其状态向量为
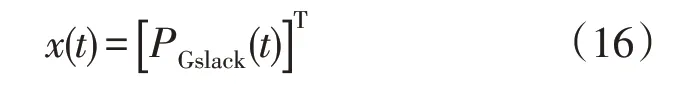
控制变量为
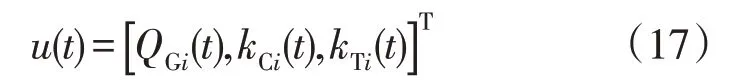
同理,利用种群S2来替代第2个目标函数与约束条件。
在解决2个目标DRPO问题时,FCSTA通过滤波技术来求解优化方案,并采用协作策略进行双种群并行搜索,在迭代过程中,解决方案在2个种群之间相互通信,并定期共享最优解决方案。1个目标函数的最优解将被另1个函数使用,这意味着将第1个目标函数的最优解用作第2个目标的初始值,并将第2个目标函数的最优解添加到第1个目标函数中,这样,模型就可以获得整体最优解,保证了处理问题的速度与准确性。最后,将有功功率损耗、电容器的投切次数与有载调压变压器抽头的动作次数作为程序的输出呈现出来。
4 仿真分析
4.1 算例介绍
为验证FCSTA优化方法解决DRPO问题的速度与有效性,本文利用IEEE 14系统来进行仿真分析。在IEEE 14系统中,假设每条母线都有相同的负荷曲线和恒定的功率因数。并联电容器组配置在母线9、10、13和14上。在母线9上有4个并联电容器,且各电容器的额定值均为0.2 p.u.。所有母线电压的上限与下限分别为1.10 p.u.与0.9 p.u.。在母线10、13和14上,并联电容器的额定功率均为0.02 p.u.。在该系统中,共有3个变压器,变比调节范围为[0.9 p.u.,1.10 p.u.],且调节步长为0.01 p.u.。无功功率控制设备允许在1天之内投切10次,系统负荷曲线见图4。
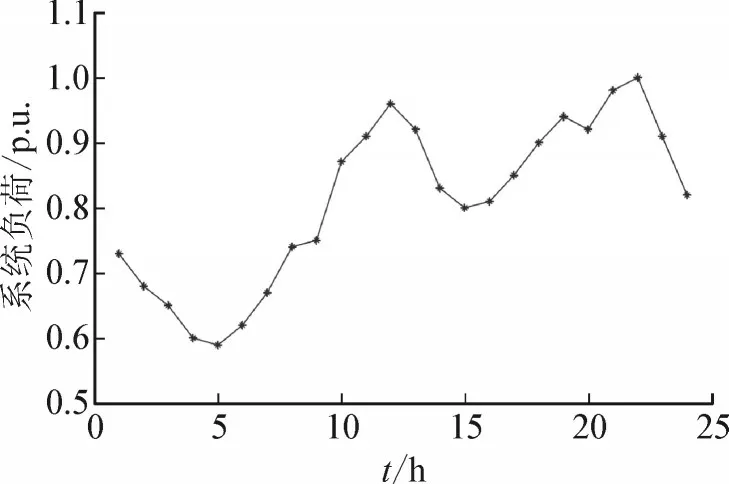
图4 IEEE 14系统负荷曲线Fig.4 IEEE 14 system load curve
4.2 仿真效果比较
为了验证FCSTA的实用性,本文选择了多种群杂交免疫遗传算法(hybrid immune genetic method,HIGM)与多蚁群算法(multiple ant colony algorithm,MACA)作为比较算法。在仿真过程中,3种算法均采用双种群并行搜索技术求解双目标DRPO模型,以比较3种算法解决DRPO问题的效果。
分别利用FCSTA、MACA和HIGM计算全天无功优化所得的功率损耗,并比较优化结果,所得网络损耗曲线见图5,由图5可知,这3种方法都可以减少功率损耗,但FCSTA全天的功率损耗最小。
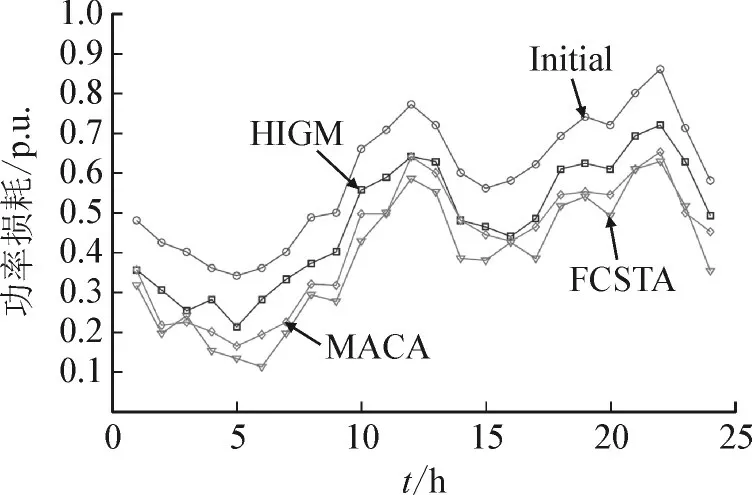
图5 全天功率损耗曲线Fig.5 Power loss curves for one day
母线9、10、13和14上并联电容器的投切次数,变压器T4-7、T4-9和T5-6的动作次数和平均功率损耗(average power loss,APL)见表1。由表1可知,MACA、HIGM和FCSTA都满足无功功率控制设备的动作次数约束。FCSTA的设备动作次数接近HIGM,但FCSTA全天的平均功率损耗要低于HIGM,这表明FCSTA具有很高的优化能力。

表1 设备动作次数Table 1 Operation numbers of equipment
采用FCSTA方法得到的离散控制变量特性见图6。
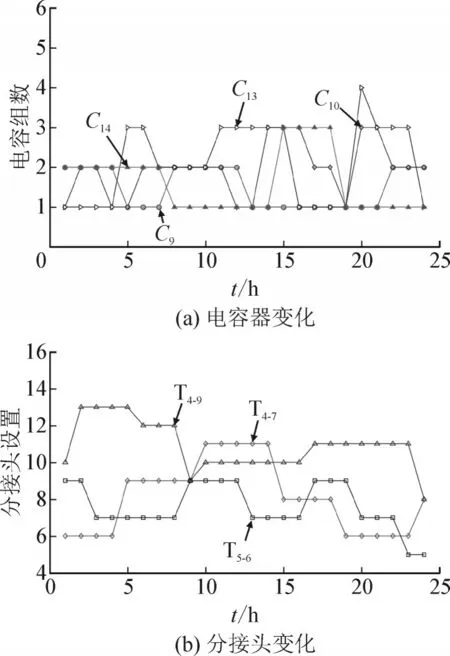
图6 动态离散控制变量设置图Fig.6 Dynamic discrete control variable setting diagram
图6(a)中,曲线C9、C10、C13和C14分别表示母线9、10、13、14上投入电容器组数变化。图6(b)中,曲线T4-7、T4-9和T5-6分别表示变压器T4-7、T4-9和T5-6的分接头位置变化。
4.3 仿真时间比较
为了比较FCSTA、MACA与HIGM 3种算法的计算速度,设置仿真迭代次数为100次,测试机配置为Inter(R)Core(TM)i7-8700K CPU@3.70GH,仿真结果见表2。

表2 仿真时间Table 2 Simulation time
由表2可知,FCSTA的平均计算时间只需要7.396 ms,相比于MACA算法和HIGM算法分别能提速37%和24%。这表明FCSTA优化方法解决DRPO问题具有一定的速度优势。
综上所述,相比于MACA和HLGM算法,FCSTA优化方法产生的平均电压偏差、平均功率损耗与平均计算时间均为最小。FCSTA优化方法能有效提高解决DRPO问题的速度和准确性。
4.4 复杂系统仿真分析
为更加充分地验证所提算法的有效性,采用东莞实际电网某53节点配电系统作为研究对象,其接线图见图7。获得的仿真结果见表3。
由表3可知,系统的复杂度并不会对所提算法的有效性产生影响,FCSTA相比于MACA和HIGM仍然具有比较明显的优势。
5 结语
针对电力系统动态无功优化约束条件繁多,难以直接解决的问题,本文提出了基于滤波协同状态转移的动态无功优化方法。经过理论分析和仿真分析后,所得的结论如下:
1)与其他算法和约束处理技术相比,FCSTA的参数少,算法结构简单,易于实现。
2)与MACA和HIGM算法相比,FCSTA具有最小的平均功率损耗。此外,相比于MACA和HIGM算法,FCSTA的平均计算时间分别能缩短37%和24%。以上表明FCSTA具有很强的优化能力,能有效提高解决DRPO问题的速度和准确性。此外,系统的复杂度并不会影响所提算法的有效性。
3)双目标DRPO模型的两个目标考虑了更多实际因素,使得该模型更有利于实际操作,这意味着该模型的适用性更加广泛,实用性更强。
