深度学习理论下的“U”型模式教学设计

蒋凤琴

[摘要]在教学中运用适合的教育促进学生思维水平的发展，使学生从浅层学习向深度学习转化，在教学过程采用“U”型教学模式，下沉环节学生体验与内化，潜行环节学生探究与归纳，上浮环节知识迁移与升华。文中以《对数的概念》教学设计为例谈如何进行高中数学U型课堂教学，培养高中生数学抽象素养。

[关键词]深度学习;U型模式;核心素养;数学抽象

适合教育的实施，有利于核心素养的培养，“U”型教学模式是导向深度教学的有效教学模式。《普通高中数学课程标准（2017年版）》中提出：“数学学科核心素养包括：数学抽象、逻辑推理、数学建模、直观想象、数学运算和数据分析。这些数学学科核心素养既相对独立、又相互交融，是一个有机的整体。”[1]

U型模式是对美国著名教育家杜威的经验教学过程理论的概括，由三个基本环节构成：下沉、潜行、上浮。一般，数学虽然需要直观的观察，以具体的模型作为理解的基础，但是数学更多地要依靠抽象思维，概念最终需要抽象概括，数学规律要求进行形式化表达，证明必须符合抽象逻辑推理。因此，在高中数学教学中，要着眼于提高学生分析理解的思维水平，使其从浅层学习向深度学习转化。

一、教材分析

（一）内容

对数的概念（人教版普通高中教科书A版数学必修第一册第122页至第123页，第128 页至第129页阅读与思考）。

（二）内容解析

对数的发明要早于指数，这是数学史上的珍闻，16-17世纪，天文、航海、工程、贸易等社会科技快速发展，对大数的计算提出了更高的要求，对数就是基于简化大数计算而产生的。本节课是对数章节的起始概念课，对上承接指数、指数函数，对下为对数函数的学习做准备。

教科书沿用了指数函数章节的问题1，通过改变旧情境的已知量和要求量，让学生感受

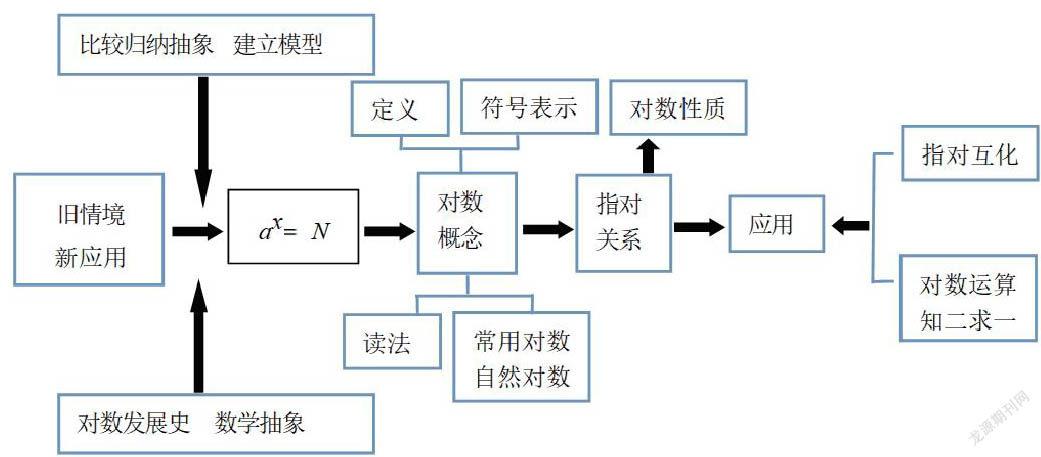
到引入与指数幂运算有关的另一种运算的必要性，由3个特例抽象出已知底数和幂求指数，即     的数学模型，在此基础上给出了对数的概念，包括定义、符号表示、读法和两个特例，再由对数的定义和指数与对数的对应关系，得出对数的有关结论。最后，通过例1指数式与对数式的互化，进一步让学生理解两种表达式的意义，通过例2求解对数表达式中真数、底数及对数的具体数值，让学生进一步认识指数运算与对数运算之间的关系。教科书第128页至第129页阅读材料《对数的发明》，让学生感受到对数发展史的神奇力量。这样的学习路径，不仅可以加强学生对对数概念的理解，而且体现了知识学习的整体性，更重要的是提高了学生的数学抽象能力，培养数学抽象核心素养。

知识结构框图如下：

（三）教学重点、难点

重点：对数的概念及指数式与对数式的互化。

难点：抽象对数的概念。

二、学情分析

首先，知识结构上，学生已经学习了幂函数、指数、指数幂的运算和指数函数，具备一定的知识基础，并熟悉研究的基本路径。能力水平上，学生经历了前面章节的学习，具备了一定的分析、归纳、概括的抽象能力。

其次，对数涉及新符号的引入，获得对数概念的过程比较抽象，学生虽然具有一定从特殊到一般，从具体到抽象的思维品质，但抽象对数概念，理解对数中的“对应”关系还是有一定困难。

三、教学过程

数学抽象的行为表现是：形成数学概念和规则，形成数学命题与模型，形成数学方法与思想，形成数学结构与体系。

（一）下沉环节：体验与内化

学生首先要将书本知识还原，还原为经验，还原的过程即知识的“下沉”过程。下沉环节是对知识表征化、表象化和具体化的过程。下沉一方面有助于学生理解知识的背景和现象，另一方面有助于建立起书本知识与学生个人经验的关联性，从而增强学生对知识的理解性。

师生活动：题1、题2投影学生学案，教师针对性点评，关注学生书写规范。题3学生独立思考，分组交流讨论。

[设计意图]题1是关于指数式与对数式互化的问题，目的在于让学生了解两类表达式的意义，体会底数、指数（对数）、幂（真数）三者之间的关系。题2通过指数幂运算求对数表达式中的真数、对数和底数的具体数值，目的是让学生进一步理解对数运算与指数运算之间的关系。题3构建模型，这是一个抽象到具体的过程，使学生更进一步认识对数模型的数学内涵，体会对数模型的适用性，从而加深对数概念的理解。

环节六：小结归纳，构建网络

问题5  请同学们带着下列问题回顾本节课学习的内容，并给出回答：

（1）你能归纳一下本节课我们是按照怎样的路径研究对数的吗？

（2）你认为利用对数可以解决怎样的问题？

（3）你是怎样理解对数的？它与指数有什么关系？

（4）我们是用什么方法获得对数性质的？

师生活动：学生先独立思考，组内交流，再全班交流，教师总结、点评、补充。

（1）通过情景由指数引出对数，类比指数，确定研究内容和研究路径。

（2）对数是达到某一数量所需要的时间。

（3）从“乘方的逆运算”、“数”、“对应”三个角度加以理解对数的概念。整体把握 数学模型，知二求一的变换，体会指数与对数的互化关系。

（4）从对数的定义，指数与对数的关系，对数几个元素之间的特殊关系，和元素特殊化获得的性质。

[设计意图]通过问题引导学生对知识进行梳理，使学生头脑中形成关于指数、对数的认知结构。通过研究路径、方法、策略的总结，把研究内容蕴含的数学思想方法提炼出来，使学生的高阶思维得到发展，培养数学核心素养。

以上教学设计体现出U型教学模式更适合学生的学习规律，结合深度学习理论能够更有效地引导学生进行知识自主建构，我们在U型教学模式中可以有多个U型循环，在大U型中设计小U型。在下沉环节，学生能建立起与自身生活体验相关的联系，迅速进入学习状态;在潜行环节，学生通过自主探究、逻辑推理，在老师指导下层层递进，提高分析能力;在上浮環节，通过例题变式设计，实现对知识的反思和进一步深化。因此，要做适合的教育，要以能否满足每一位学生成长需求为标准，不能丢掉了数学的根本，使用U型教学模式，能够提升思维，提高课堂教学效果。

参考文献

[1][2]郭元祥.深度教学研究[M].福州：福建教育出版社，2019.10：228-229.